Matematikte
Gerçel sayılar (veya
reel sayılar) kümesi, oranlı sayılar (rasyonel sayılar) kümesinin standart metriğe göre bütünlenmesiyle elde edilen kümedir. Reel sayılar kümesi

sembolüyle gösterilir. Daha basit söyleyişle, bir gerçel sayı, ondalık gösteriminde virgülden sonra sonsuz basamağı olan bir sayıdır.
Her oranlı sayı (rasyonel sayı) bir gerçel sayıdır; virgülden sonra tekrar eden ondalık açılımı vardır (0 dahil). Örneğin:

veya
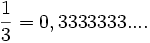
veya
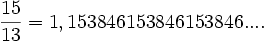
eşitliklerinde olduğu gibi. Burada dikkat edilmesi gereken, ondalık basamaklardaki rakamların bir süre sonra bloklar halinde periyodik tekrar etme özelliğidir. Bu şöyle ispatlanabilir:
m,
n iki tamsayı (
n pozitif) olsun.
m/n oranlı sayısı ondalık ifade edilmek istendiğinde,
m 'yi
n 'ye bölerken (bölme algoritmasını uygularken) ilk adımda kalan 0 ile n arasında olacaktır. Kalanın yanına sıfırlar ekleyip bölmeye devam edilecek ve bir sonraki adımda kalan yine 0 ile n arasında olacaktır. Sonsuz adımda sonlu sayıda değer alabilen kalanlar, bir süre sonra aynı değeri alacak ve kendini tekrar edecektir.
Oranlı sayılardan gerçel sayıları elde etme işlemiyse oranlı sayılara ondalık açılımındaki rakamların devirsel tekrar etmediği sayıların eklenmesi olarak düşünülebilir. Bu tür sonradan elde ettiğimiz gerçel sayılara irrasyonel sayılar denir.
İrrasyonel sayıların varlığı
Düzlemde herhangi bir doğru parçası alıp buna birim uzunluk diyelim. Tamsayılarla bu doğru parçasının katları birebir eşlensin. Alınan bir doğrunun üzerinde bu tamsayı uzunlukları ve olası tüm oranları (oranlı sayılar) işaretlensin. Gösterilebilir ki, herhangi iki oranlı sayı arasında sonsuz çoklukta oranlı sayı vardır. Demek oluyor ki, alınan doğru üzerinde birbirlerine istenildiği kadar yakın ve oranlı sayıları temsil eden iki nokta (oranlı nokta) arasında , sonsuz çoklukta oranlı nokta vardır.
Bu tür noktaların, dolayısıyla uzunlukların varlığını ispatlamak için, kenar uzunluğu 1 birim olan bir karenin köşegen uzunluğunu (
x) sayı doğrusu üzerinde işaretleyelim.
x uzunluğu, oranlı bir sayı değildir, yani
p ve
q birer tamsayı olmak üzere
p/q şeklinde gösterilemeyen bir sayıdır; bu sayı

olarak gösterilecektir.
Kabul edelim ki
x=p/q olsun. Bundan başka, bu kesrin artık kısaltılamayan bir kesir olduğunu farz edelim, yani
p ve
q aralarında asal olsunlar. Başka bir deyişle, bunların 1'den başka ortak bölenleri bulunmasın. Pisagor teoremi sayesinde
x2=2=p2/q2 elde edilir. Dolayısıyla 2
q2=p2 olur.
p ve
q aralarında asal olduğu için 2,
p 'yi bölmek zorundadır. Böylece eşitliğin sağ tarafı 4'e bölünür. Sol tarafının da dörde bölünmesi gerekeceğinden
q da 2'ye bölünmek zorunda kalır. Hem
p hem de
q sayıları 2'ye bölünebiliyorsa, aralarında asallık kabulüyle çelişkili bir sonuç bulunmuş olur. O halde
x 'in oranlı bir sayı olduğu kabulünden vazgeçmek gerekecektir.
Bu ispat, bir Pisagorcu olan Hippasus'a atfedilmektedir (İ.Ö: 5. yüzyıl). İrrasyonel sayıların varlığının ilk antik Yunan matematikçi Pisagor'un okulu tarafından anlaşılmış olduğu görüşü yaygındır. Fakat Pisagor bu sayıların evrenin düzenine aykırı olduğunu düşünmüş ve öğrencilerine bu sayıların varlığını açıklamayı yasaklamıştır. Rivayete göre Hippasus'u o öldürtmüştür.
İrrasyonel Sayılara Örnekler 
,

,

, π ,
e,
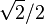
birer irrasyonel sayıdır. İki irrasyonel sayının toplamı, çarpımı, yine bir irrasyonel sayı olmak zorunda değildir
Gerçek sayıların kurulması Belitlerle inşa
Aşağıdaki belitler aracılığıyla kurulan gerçel sayılar sistemi, bütün sıralı bir cisimdir. Kümeler kuramının Zermelo-Fraenkel belitleri ile inşası kabul edilerek, aşağıdaki belitleri sağlayan bir modelin varlığı ve bunları sağlayan herhangi iki modelin birbirine izomorfik olduğu gösterilebilir.
Gerçel sayılar sistemi bir
R kümesi, içinde 0 ve 1 adlı iki öğe (eleman), + ve x ile gösterilen iki tane ikili işlem ve ≤ olarak gösterilen bir ikili bağıntıdan oluşuktur. Bunlar aşağıdaki belitleri sağlar:
1. (
R, +, x) bir cisimdir.
2. (
R, ≤) tamamen sıralı bir kümedir.
3. ≤ bağıntısı + ve x işlemleri altında korunur:
- a, b ve c R 'de, ve a ≤ b olmak üzere a + c ≤ b + c olmalıdır.
- a, b R 'de, ve 0 ≤ a, 0 ≤ b olmak üzere 0 ≤ a x b olmalıdır.
4. ≤ sıralaması bütündür:
R'nin boşküme olmayan ve yukarıdan sınırlı her alt kümesi, en küçük bir üst sınıra sahiptir.
Aşağıda gerçel sayı sistemi için kimi model inşaları bulunmaktadır. Bunların her biri bir diğeriyle, yukarıda sözü edilen anlamda aynıdır. Cauchy dizileriyle inşa Dedekind kesimleriyle inşa Tamsayılar grubunu kullanarak inşa Bazı Yan Bilgiler - Tam kare olmayan hiçbir doğal sayının karekökü oranlı değildir.
- Oranlı sayılar kümesi sayılabilir olmasına karşılık gerçel sayılar kümesi sayılamazdır.
- Gerçel sayılar "cebirsel sayılar" ve "aşkın sayılar" (transcendental) olarak ikiye ayrılırlar. Cebirsel bir gerçel sayı, tamsayı katsayılı bir polinomun kökü olabilen bir sayıdır; örneğin: x2 - 2 polinomunu 0 yapan değerlerden biri (kök)
 'dir. x - 2 polinomunun kökü 2'dir. Dolayısıyla
'dir. x - 2 polinomunun kökü 2'dir. Dolayısıyla  ve 2 cebirsel sayılardır. Ancak π ve e sayıları herhangi bir polinomun kökü olamazlar; bunlar aşkın sayılardır.
ve 2 cebirsel sayılardır. Ancak π ve e sayıları herhangi bir polinomun kökü olamazlar; bunlar aşkın sayılardır.
İspat
Doğal sayıları için
nx≤y dir. Bu durumda
y/x,
N doğal sayılar kümesi için bir üst sınırdır. Böylece
N,
R nin boş olmayan bir altkümesi olup üstten sınırlıdır ve en küçük üst sınır özelliğinden bir
s supremuma (e.k.ü.s.'e) sahiptir.
s-1< s olduğundan
s-1,
N için bir üst sınır olamaz. Bu yüzden,
N 'nin
s-1 den büyük olan bir
n elemanı var olmalıdır. Ancak eğer
n>s-1 ise
n+1>solur. Bu da
s 'nin
N nin supremumu olması ile çelişir. Bu da bizi varsayımımızın karşıtına götürür. Yani her bir
n için
n<=x olamaz.

 Gerçel (Reel) Sayılar
Gerçel (Reel) Sayılar sembolüyle gösterilir. Daha basit söyleyişle, bir gerçel sayı, ondalık gösteriminde virgülden sonra sonsuz basamağı olan bir sayıdır.
sembolüyle gösterilir. Daha basit söyleyişle, bir gerçel sayı, ondalık gösteriminde virgülden sonra sonsuz basamağı olan bir sayıdır. veya
veya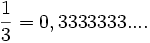 veya
veya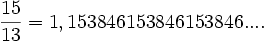 eşitliklerinde olduğu gibi. Burada dikkat edilmesi gereken, ondalık basamaklardaki rakamların bir süre sonra bloklar halinde periyodik tekrar etme özelliğidir. Bu şöyle ispatlanabilir: m, n iki tamsayı (n pozitif) olsun. m/n oranlı sayısı ondalık ifade edilmek istendiğinde, m 'yi n 'ye bölerken (bölme algoritmasını uygularken) ilk adımda kalan 0 ile n arasında olacaktır. Kalanın yanına sıfırlar ekleyip bölmeye devam edilecek ve bir sonraki adımda kalan yine 0 ile n arasında olacaktır. Sonsuz adımda sonlu sayıda değer alabilen kalanlar, bir süre sonra aynı değeri alacak ve kendini tekrar edecektir.
eşitliklerinde olduğu gibi. Burada dikkat edilmesi gereken, ondalık basamaklardaki rakamların bir süre sonra bloklar halinde periyodik tekrar etme özelliğidir. Bu şöyle ispatlanabilir: m, n iki tamsayı (n pozitif) olsun. m/n oranlı sayısı ondalık ifade edilmek istendiğinde, m 'yi n 'ye bölerken (bölme algoritmasını uygularken) ilk adımda kalan 0 ile n arasında olacaktır. Kalanın yanına sıfırlar ekleyip bölmeye devam edilecek ve bir sonraki adımda kalan yine 0 ile n arasında olacaktır. Sonsuz adımda sonlu sayıda değer alabilen kalanlar, bir süre sonra aynı değeri alacak ve kendini tekrar edecektir. olarak gösterilecektir.
olarak gösterilecektir. ,
,  , π , e,
, π , e, 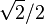 birer irrasyonel sayıdır. İki irrasyonel sayının toplamı, çarpımı, yine bir irrasyonel sayı olmak zorunda değildir
birer irrasyonel sayıdır. İki irrasyonel sayının toplamı, çarpımı, yine bir irrasyonel sayı olmak zorunda değildir
