Ziyaretçi
Matematiksel Beklenti
Olasılık kuramı bilim dalında matematiksel beklenti veya beklenen değer veya ortalama birçok defa tekrarlanan ve her tekrarda mümkün tüm olasılıklarını değiştirmeyen rastgele deneyler sonuçlarından beklenen ortalama değeri temsil eder. Bir ayrık rassal değişkennin alabileceği bütün sonuç değerlerin (bazan ödemelerin) olasılıklarıyla çarpılması ve bu işlemin bütün değerler üzerinden toplanmasıyla elde edilen değerdir. Bir sürekli rassal değişken için rassal değişken ile olasılık yoğunluk fonksiyonunun çarpımının aralığı belirsiz entegralidir. Fakat dikkat edilmelidir ki bu değerin genel pratik anlamla rasyonel olarak beklenmesi pek uygun olmayabilir, çünkü matematiksel beklentiin olasılığı çok düşük belki sıfıra çok yakın olabilir ve hatta pratikte matematiksel beklenti bulunmaz. Ağırlıklı ortalama olarak da düşünülebilir ki değerler ağırlık katsayıları verilen olasılık kütle fonksiyonu veya olasılık yoğunluk fonksiyonudur.
Tanım
Pratik örneklerle belirleme
Matematiksel beklenti, beklenen değer işlemcisi E ile gösterilir. Hileli yanlı olmayan bir altı-köşeli zar atılırsa mümkün değerler (1 2 3 ...6) olup herbir değerin olasılığı (1/6) olur. Böylece tek bir zar atımı için matematiksel beklenti

olur. Dikkat edilirse bu beklenen değer kesirsel olup gerçekte mümkün olan bir sonuç değildir.
Matematiksel beklenti kavramının pratikte çok kullanıldığı bir alan kumar oyunlarıdır. Bir Amerikan tipi rulet oyunu tekerleğinde dönen ufak topun herbirine aynı olasılıkla girip kalabileceği numara verilmiş 38 küçük delik vardir. Eğer topun gireceği deliğin numarası için bahse girilirse ve bu bahiste doğru bilişte kazanç bahis-olasılığı ile 35-te-1 olur; yani sonuç bahisin 36 misli olup koyulan para kaybedilmeyip 35 misli daha kazanç sağlanır. Herbir sonuça bahis için iki mümkün olay kaybetme veya kazanma ve bu iki mümkün olay için (kumar için çok kere bahis-olasılığı ile ifade edilen) olasılık vardır. Toplam mümkün 38 tane sonuç olabileceğine göre, tek bir numaraya 1TL konulursa kazancın beklenen değerini bulmak için önce kaybetme para değeri ile kaybetme bahis-olasılığı çarpımı; sonra kazanma para değeri ile kazanma bahis-olasılığı çarpımı bulunup bu ikisinin toplamı alınır; yani

1TL bahis için mali durumdaki değişme, kaybedince −1TL ve kazanınca 35TL olur. Böylece, ortalama olarak, her yapılan 1TL değerde bahis için zarar 5 kuruşu biraz geçecektir ve 1TLlik bahsin matematiksel beklentisi 0,9474TL olacaktır. Kumar oyunlarında, bir oyun için beklenen değer bahse koyulan değere eşitse (yani kumar oynayanın beklenen değeri 0 ise) o kumar oyunu "adil oyun" diye isimlendirilir.
Matematiksel tanım
Genel olarak, eğer
 olan bir olasılık uzayı içinde bir rassal değişken ise, o halde
olan bir olasılık uzayı içinde bir rassal değişken ise, o halde
 in matematiksel beklentisi, notasyon olarak değer işlemcisi E kulanarak,
in matematiksel beklentisi, notasyon olarak değer işlemcisi E kulanarak, 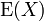 veya
veya
bazan , or
, or 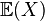 olarak yazılır ve şöyle tanımlanır:
olarak yazılır ve şöyle tanımlanır:

Burada Lebesgue entegrasyonu uygulanmıştır. Dikkat edilmelidir ki bütün rassal değişkenler için matematiksel beklenti değeri bulunmaz; bu entegral bulunmayıp anlamsız ise (örneğin Cauchy dağılımı için) o halde beklenen değer de tanımlanamaz ve anlamsızdır. Ayni olasılık dağılımı gösteren iki rassal değişken için matematiksel beklenti aynıdır.
Eğer X bir olasılık kütle fonksiyonu p(x) olan bir ayrık rassal değişken ise, o halde beklenen değer şu olur:

Eğer X bir sürekli rassal değişken olup olasılık yoğunluk fonksiyonu f(x) ise, o halde matematiksel beklenti veya beklenen deger şöyle bulunur:
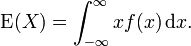
Olasılık yoğunluk fonksiyonu f(x) olan rassal değişken X için herhangi bir rastgele seçilmiş fonksiyon g(X) için matematiksel beklenti veya beklenen değer şöyle verilir:

Özellikler
Sabitler
Bir sabit k için matematiksel beklenti veya beklenen deger sabitin kendi değerine eşittir:

Monotonluk
Eğer X ve Y iki rassal değişken ve geçerli ise, o halde
geçerli ise, o halde
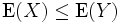 . olur.
. olur.
Doğrusallık
Beklenen değer işlemcisi şu anlamlarda doğrusal olur:
şu anlamlarda doğrusal olur:
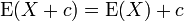 ;
; ;
;
Bu üç denklem sonucları birleştirilirse şu ifadeler bulunur:

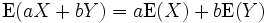
Burada X ile Y aynı olasılık uzayında bulunan rassal değişkenler ve a ile b reel sayılardır.
Yinelenmiş beklenti
Ayrık rassal değişken için yinelenmiş beklenti
Herhangi iki ayrık rassal değişken X,Y için koşullu beklenti şöyle tanımlanabilir:
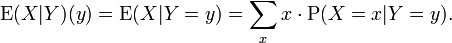
Bundan ifadesinin y üzerinde bir fonksiyon olduğu anlaşılır.
ifadesinin y üzerinde bir fonksiyon olduğu anlaşılır.
O zaman X için beklenti şu ifadeyi tatmin eder:
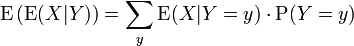
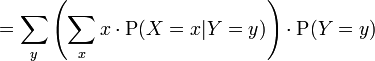

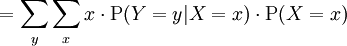



Böylece şu denklem ortaya çıkartılır:

Bu denklemin sağ tarafı yinelenmiş beklenti adı ile anılır ve bazan kule kuralı adı da verilir. Bu toplam beklenti yasası maddesinde de incelenmiştir.
Sürekli rassal değişken için yinelenmiş beklenti
Herhangi iki sürekli rassal değişken X,Y için de sonuçlar ayrık rassal değişkenler halinin tamamiyle benzeridir. Koşullu beklenti tanımı eşitsizlikleri kullanır; olasılık yoğunluk fonksiyonları ile entegralleri olasılık kütle fonksiyonları ile toplamalar yerlerini alırlar. Sonunda aynı sonuç ortaya çıkar:

Eşitsizlik
Eğer bir rassal değişken X diğer bir rassal değişken olan Yden daha az veya ona eşitse ise,
Eğer , o halde
, o halde 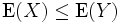 olur. Özellikle
olur. Özellikle 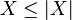 ve
ve 
oldukları için, bir rassal değişkenin matematiksel beklentisinin (veya beklenen değerinin) mutlak değeri, mutlak değerinin matematiksel beklentisinden daha küçük olur veya ona eşittir:
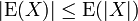
Simgelenme
( ) koşuluna uyan her bir negatif olmayan reel değerli rassal değişken X ve pozitif reel sayı α için şu formül herzaman geçerlidir:
) koşuluna uyan her bir negatif olmayan reel değerli rassal değişken X ve pozitif reel sayı α için şu formül herzaman geçerlidir:

Özellikle bu daha da kısa olarak şöyle ifade edilebilir:

Çarpımsallık özelliği olmama
Genel olarak E beklenen değer işlemcisinin çarpımsallık özelliği bulunmaz, yani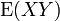 ile
ile 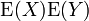 birbirine mutlaka eşit olmaz. Eğer çarpımsallık özelliği bulunursa, bu halde X ve Y rassal değişkenleri birbiri arasinda korelasyon bulunmayan değişkenler olarak tanımlanırlar. Aralarında bağımsızlık bulunan değişkenlerin birbirleri arasında korelasyon bulunmayan değişkenlere en önemli örneğin sağlarlar. Genellikle çarpımsal olmama özelliği kovaryasyon ve korelasyon analizlerine önemli bir neden sağlar.
birbirine mutlaka eşit olmaz. Eğer çarpımsallık özelliği bulunursa, bu halde X ve Y rassal değişkenleri birbiri arasinda korelasyon bulunmayan değişkenler olarak tanımlanırlar. Aralarında bağımsızlık bulunan değişkenlerin birbirleri arasında korelasyon bulunmayan değişkenlere en önemli örneğin sağlarlar. Genellikle çarpımsal olmama özelliği kovaryasyon ve korelasyon analizlerine önemli bir neden sağlar.
Fonksiyonel daimilik olmaması
Genel olarak beklenen değer işlemcisi E'ye ve rassal değişkenler için fonksiyonlara değişmeli işlem uygulanamaz; yani
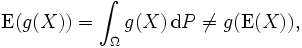
Bu konuyla ilişkili en önemli konu konveks (veya konkav) fonksiyonlarla ilişkili olarak Jensen'in eşitsizliğidir.
Matrisler için beklenti
Matris matematiğine göre, X dereceli bir matris ise o halde bu matrisin matematiksel beklentisi (veya beklenen değeri) matris elamanlarının ayrı ayrı matematiksel beklentilerinin (veya beklenen değerlerinin) matrisi olur:
dereceli bir matris ise o halde bu matrisin matematiksel beklentisi (veya beklenen değeri) matris elamanlarının ayrı ayrı matematiksel beklentilerinin (veya beklenen değerlerinin) matrisi olur:

Bu sonuç kovaryans matrisleri için kullanılır.
Sponsorlu Bağlantılar
Tanım
Pratik örneklerle belirleme
Matematiksel beklenti, beklenen değer işlemcisi E ile gösterilir. Hileli yanlı olmayan bir altı-köşeli zar atılırsa mümkün değerler (1 2 3 ...6) olup herbir değerin olasılığı (1/6) olur. Böylece tek bir zar atımı için matematiksel beklenti

olur. Dikkat edilirse bu beklenen değer kesirsel olup gerçekte mümkün olan bir sonuç değildir.
Matematiksel beklenti kavramının pratikte çok kullanıldığı bir alan kumar oyunlarıdır. Bir Amerikan tipi rulet oyunu tekerleğinde dönen ufak topun herbirine aynı olasılıkla girip kalabileceği numara verilmiş 38 küçük delik vardir. Eğer topun gireceği deliğin numarası için bahse girilirse ve bu bahiste doğru bilişte kazanç bahis-olasılığı ile 35-te-1 olur; yani sonuç bahisin 36 misli olup koyulan para kaybedilmeyip 35 misli daha kazanç sağlanır. Herbir sonuça bahis için iki mümkün olay kaybetme veya kazanma ve bu iki mümkün olay için (kumar için çok kere bahis-olasılığı ile ifade edilen) olasılık vardır. Toplam mümkün 38 tane sonuç olabileceğine göre, tek bir numaraya 1TL konulursa kazancın beklenen değerini bulmak için önce kaybetme para değeri ile kaybetme bahis-olasılığı çarpımı; sonra kazanma para değeri ile kazanma bahis-olasılığı çarpımı bulunup bu ikisinin toplamı alınır; yani

1TL bahis için mali durumdaki değişme, kaybedince −1TL ve kazanınca 35TL olur. Böylece, ortalama olarak, her yapılan 1TL değerde bahis için zarar 5 kuruşu biraz geçecektir ve 1TLlik bahsin matematiksel beklentisi 0,9474TL olacaktır. Kumar oyunlarında, bir oyun için beklenen değer bahse koyulan değere eşitse (yani kumar oynayanın beklenen değeri 0 ise) o kumar oyunu "adil oyun" diye isimlendirilir.
Matematiksel tanım
Genel olarak, eğer

 olan bir olasılık uzayı içinde bir rassal değişken ise, o halde
olan bir olasılık uzayı içinde bir rassal değişken ise, o halde  in matematiksel beklentisi, notasyon olarak değer işlemcisi E kulanarak,
in matematiksel beklentisi, notasyon olarak değer işlemcisi E kulanarak, 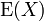 veya
veya bazan
 , or
, or 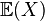 olarak yazılır ve şöyle tanımlanır:
olarak yazılır ve şöyle tanımlanır:
Burada Lebesgue entegrasyonu uygulanmıştır. Dikkat edilmelidir ki bütün rassal değişkenler için matematiksel beklenti değeri bulunmaz; bu entegral bulunmayıp anlamsız ise (örneğin Cauchy dağılımı için) o halde beklenen değer de tanımlanamaz ve anlamsızdır. Ayni olasılık dağılımı gösteren iki rassal değişken için matematiksel beklenti aynıdır.
Eğer X bir olasılık kütle fonksiyonu p(x) olan bir ayrık rassal değişken ise, o halde beklenen değer şu olur:

Eğer X bir sürekli rassal değişken olup olasılık yoğunluk fonksiyonu f(x) ise, o halde matematiksel beklenti veya beklenen deger şöyle bulunur:
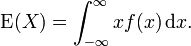
Olasılık yoğunluk fonksiyonu f(x) olan rassal değişken X için herhangi bir rastgele seçilmiş fonksiyon g(X) için matematiksel beklenti veya beklenen değer şöyle verilir:

Özellikler
Sabitler
Bir sabit k için matematiksel beklenti veya beklenen deger sabitin kendi değerine eşittir:

Monotonluk
Eğer X ve Y iki rassal değişken ve
 geçerli ise, o halde
geçerli ise, o halde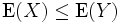 . olur.
. olur.Doğrusallık
Beklenen değer işlemcisi
 şu anlamlarda doğrusal olur:
şu anlamlarda doğrusal olur: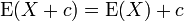 ;
; ;
;
Bu üç denklem sonucları birleştirilirse şu ifadeler bulunur:

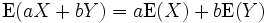
Burada X ile Y aynı olasılık uzayında bulunan rassal değişkenler ve a ile b reel sayılardır.
Yinelenmiş beklenti
Ayrık rassal değişken için yinelenmiş beklenti
Herhangi iki ayrık rassal değişken X,Y için koşullu beklenti şöyle tanımlanabilir:
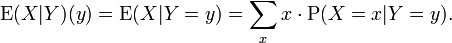
Bundan
 ifadesinin y üzerinde bir fonksiyon olduğu anlaşılır.
ifadesinin y üzerinde bir fonksiyon olduğu anlaşılır.O zaman X için beklenti şu ifadeyi tatmin eder:
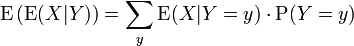
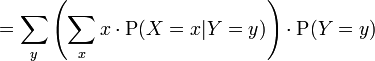

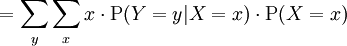



Böylece şu denklem ortaya çıkartılır:

Bu denklemin sağ tarafı yinelenmiş beklenti adı ile anılır ve bazan kule kuralı adı da verilir. Bu toplam beklenti yasası maddesinde de incelenmiştir.
Sürekli rassal değişken için yinelenmiş beklenti
Herhangi iki sürekli rassal değişken X,Y için de sonuçlar ayrık rassal değişkenler halinin tamamiyle benzeridir. Koşullu beklenti tanımı eşitsizlikleri kullanır; olasılık yoğunluk fonksiyonları ile entegralleri olasılık kütle fonksiyonları ile toplamalar yerlerini alırlar. Sonunda aynı sonuç ortaya çıkar:

Eşitsizlik
Eğer bir rassal değişken X diğer bir rassal değişken olan Yden daha az veya ona eşitse ise,
Eğer
 , o halde
, o halde 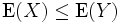 olur. Özellikle
olur. Özellikle 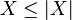 ve
ve 
oldukları için, bir rassal değişkenin matematiksel beklentisinin (veya beklenen değerinin) mutlak değeri, mutlak değerinin matematiksel beklentisinden daha küçük olur veya ona eşittir:
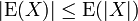
Simgelenme
(
 ) koşuluna uyan her bir negatif olmayan reel değerli rassal değişken X ve pozitif reel sayı α için şu formül herzaman geçerlidir:
) koşuluna uyan her bir negatif olmayan reel değerli rassal değişken X ve pozitif reel sayı α için şu formül herzaman geçerlidir:
Özellikle bu daha da kısa olarak şöyle ifade edilebilir:

Çarpımsallık özelliği olmama
Genel olarak E beklenen değer işlemcisinin çarpımsallık özelliği bulunmaz, yani
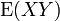 ile
ile 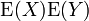 birbirine mutlaka eşit olmaz. Eğer çarpımsallık özelliği bulunursa, bu halde X ve Y rassal değişkenleri birbiri arasinda korelasyon bulunmayan değişkenler olarak tanımlanırlar. Aralarında bağımsızlık bulunan değişkenlerin birbirleri arasında korelasyon bulunmayan değişkenlere en önemli örneğin sağlarlar. Genellikle çarpımsal olmama özelliği kovaryasyon ve korelasyon analizlerine önemli bir neden sağlar.
birbirine mutlaka eşit olmaz. Eğer çarpımsallık özelliği bulunursa, bu halde X ve Y rassal değişkenleri birbiri arasinda korelasyon bulunmayan değişkenler olarak tanımlanırlar. Aralarında bağımsızlık bulunan değişkenlerin birbirleri arasında korelasyon bulunmayan değişkenlere en önemli örneğin sağlarlar. Genellikle çarpımsal olmama özelliği kovaryasyon ve korelasyon analizlerine önemli bir neden sağlar.Fonksiyonel daimilik olmaması
Genel olarak beklenen değer işlemcisi E'ye ve rassal değişkenler için fonksiyonlara değişmeli işlem uygulanamaz; yani
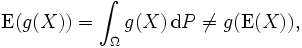
Bu konuyla ilişkili en önemli konu konveks (veya konkav) fonksiyonlarla ilişkili olarak Jensen'in eşitsizliğidir.
Matrisler için beklenti
Matris matematiğine göre, X
 dereceli bir matris ise o halde bu matrisin matematiksel beklentisi (veya beklenen değeri) matris elamanlarının ayrı ayrı matematiksel beklentilerinin (veya beklenen değerlerinin) matrisi olur:
dereceli bir matris ise o halde bu matrisin matematiksel beklentisi (veya beklenen değeri) matris elamanlarının ayrı ayrı matematiksel beklentilerinin (veya beklenen değerlerinin) matrisi olur:
Bu sonuç kovaryans matrisleri için kullanılır.

 Matematiksel Beklenti
Matematiksel Beklenti
