Cauchy-Riemann denklemleri
Matematiğin bir dalı olan karmaşık analizde Augustin Louis Cauchy ve Bernhard Riemann'a atfen Cauchy-Riemann denklemleri olarak adlandıran denklemler, türevlenebilir bir fonksiyonun açık bir kümede holomorfik fonksiyon olması için gerekli ve yeterli şartları sağlayan kısmi diferansiyel denklemlerdir. Bu denklemler sistemi ilk defa Jean le Rond d'Alembert'in 1752 yılındaki çalışmasında ortaya çıkmıştır. Daha sonra, 1777 yılındaki çalışmasıyla Leonhard Euler bu sistemi analitik fonksiyonlarla ilişkilendirmiştir. Cauchy ise bu sistemi 1814'teki çalışmasındaki fonksiyonlar teorisinde kullanmıştır. Riemann'ın fonksiyonlar teorisi üzerine olan doktora tezinin tarihi ise 1851'dir.

Bir gerçel değerli fonksiyon çifti u(x,y) ve v(x,y) için yazılan Cauchy-Riemann denklemleri aşağıdaki gibidir:
(1a) ve
(1b) Genelde u ve v çifti, karmaşık değerli bir f(x + iy) = u(x,y) + iv(x,y) fonksiyonunun gerçel ve sanal kısımları olarak alınır. u ve v, C 'nin açık bir kümesinde sürekli şekilde türevlenebilir bir fonksiyon olsun. O zaman, f=u+iv ancak ve ancak u ve v Cauchy-Riemann denklemlerini ((1a)'yı ve (1b)'yi) sağlarsa, holomorfiktir.

Yorumu ve formülasyonu


Açıkorur gönderimler

Cauchy-Riemann denklemleri çeşitli yollarla genelde tekrar formüle edilirler. Birincisi,
(2) karmaşık formunda yazılabilirler.
Bu formda, denklemler yapısal olarak Jakoben matrisinin, ve olacak şekilde,
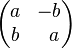
formunda olmasına karşılık gelir. Bu formdaki bir matris bir karmaşık sayının matris temsilidir. Geometrik olarak, böyle bir matris her zaman homotetisi olan bir rotasyonun bileşkesidir ve bilhassa açıları korur. Sonuç olarak, türevi sıfırdan farklı, Cauchy-Riemann denklemlerini sağlayan bir fonksiyon düzlemdeki eğriler arasındaki açıyı korur. Yani, Cauchy-Riemann denklemleri bir fonksiyonun açıkorur gönderim olması için olan koşullardır.

Karmaşık eşleniğin bağımsız olması

Denklemler bazen tek bir denklem olarak yazılır:
(3) Burada, türev operatörü
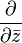
olarak tanımlanmıştır.
Bu formda, Cauch-Riemann denklemleri "f, değişkeninden bağımsızdır" olarak yorumlanabilir.

Karmaşık türevlilik

Cauchy-Riemann denklemleri bir fonksiyonun karmaşık türevli (veya holomorfik) olması için gerekli ve yeterli bir koşuldur (Ahlofors 1953, §1.2 ). Daha ayrıntılı bir şekilde,
f(z) = u(z) + iv(z) z∈C karmaşık sayısının fonksiyonu olsun. O zaman, f 'nin z0 noktasında karmaşık türevi eğer limit varsa
olarak tanımlanır.
Eğer bu limit varsa, limit reel eksen veya sanal eksen boyunca h→0 alınarak hesaplanabilir ve her iki durumda da aynı sonucu vermelidir. Reel eksen boyunca yaklaşılırsa
elde edilir. Diğer taraftan sanal eksen boyunca yaklaşılırsa
elde edilir. İki eksen boyunca alınan türevlerin eşitliği
ifadesini verecektir. Farkedilirse bu, z0 noktasındaki (2) nolu Cauchy-Riemann denklemidir.
Tersine, f:C → C, R2 'de türevli olarak algılanırsa, o zaman f ancak ve ancak Cauchy-Riemann denklemleri sağlanırsa karmaşık türevlidir.



Diğer temsiller

Cauchy-Riemann denklemlerinin diğer temsilleri diğer koordinat sistemlerinde de ortaya çıkmaktadır. Sürekli şekilde türevlenebilir bir u ve v fonksiyon çifti için (1a) ve (1b) sağlanıyorsa, o zaman 'nin birim dik ve pozitif yönlü olduğu herhangi (n(x,y), s(x,y)) koordinatı için de
eşitlikleri sağlanır. Sonuç olarak, özellikle, z=reiθ olarak verilen kutupsal koordinatlar sisteminde, denklemler
halini alır.
f için bu iki denklem birleştirildiğinde
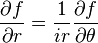
elde edilir.

Homojen olmayan denklemler

Homojen olmayan Cauchy-Riemann denklemleri, R2 'nin açık bir altkümesinde verilmiş α(x,y) ve β(x,y) için, bilinmeyen iki gerçel değişkenli bir u(x,y) ve v(x,y) fonksiyon çiftinin iki denkleminden oluşur:
Bu denklemler genellikle bir denklemde toplanırlar (f=u+iv ve φ=(α+iβ)/2):
Eğer φ, Ck ise, o zaman herhangi sınırlı bir D bölgesinin kapanışında φ sürekli olduğu sürece, homojen olmayan denklem D 'de açık olarak çözülebilir. Aslında Cauchy integral formülü kullanılarak her ζ∈D için
ifadesi elde edilir.

Genelleştirmeler


Goursat teoremi ve genelleştirmeleri

Ayrıca bakınız: Cauchy-Goursat teoremi f = u+iv, f : R2 → R2 fonksiyonu olarak karmaşık değerli, türevlenebilir bir fonksiyon olsun. O zaman Goursat teoremi, f 'nin açık karmaşık bir Ω bölgesinde ancak ve ancak fonksiyon Cauchy-Riemann denklemlerini sağlarsa analitik olacağını ifade eder (Rudin 1966, Teorem 11.2). Özelde, f 'nin sürekli türevliliği varsayılmak zorunda değildir (Dieudonné 1969, §9.10, Al. 1).
Goursat teoremi 'nin varsayımları önemli bir ölçüde zayıflatılabilir. f=u+iv açık bir Ω kümesinde sürekliyse ve f 'nin Ω 'da x ve y 'ye göre kısmi türevleri varsa, o halde f holomorfiktir (ve bu yüzden analitiktir). Bu sonuç Looman–Menchoff teoremi olarak bilinir.
f 'nin Ω üzerinde Cauchy-Riemann denklemlerini sağlaması varsayımı çok önemlidir. Bir noktada Cauchy-Riemann denklemlerini sağlayan ancak analitik olmayan bir fonksiyon inşa etmek mümkündür (mesela f(z) = z5/|z|4). Benzer bir şekilde, aşağıdaki örneğin de gösterdiği gibi, Cauchy-Riemann denklemlerinin yanında (süreklilik gibi) bazı ek varsayımlara da ihtiyaç vardır (örnek Looman 1923, sf. 107'dedir.):
Cauchy-Riemann denklemlerini sağlar ancak z=0 noktasında sürekli değildir.
Yine de, bir fonksiyon açık bir küme üzerinde Cauchy-Riemann denklemlerini zayıf bir anlamda sağlıyorsa, o zaman fonksiyon analitiktir. Daha kesin bir anlamda (Gray Morris 1978, Teorem 9),

• f(z), Ω⊂C açık bölgesinde yerel olarak integrallenebiliyorsa ve zayıf bir şekilde Cauchy-Riemann denklemlerini sağlıyorsa, o zaman f, Ω içindeki analitik bir fonksiyonla hemen hemen her yerde aynıdır.

Çok değişkenler

Cauchy-Riemann denklemlerinin çok karmaşık değişkenlere uygun genelleştirmeleri de vardır. Kısmi diferansiyel denklemleri önemli bir [artık belirtilmiş sistemleri]]ni oluştururlar. Çoğu zaman formüle edildiği gibi
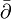d-bar operatörü holomorfik fonksiyonları imha eder. Bu doğrudan
alınarak şu genelleştirmeyi yapar:


Dalga denklemi


1 boyutlu dalga denklemi.


Dalga denklemi fizikte çok önemli yere sahip bir kısmi diferansiyel denklemdir. Bu denklemin çözümlerinden, ses, ışık ve su dalgalarının hareketlerini betimleyen fiziksel nicelikler çıkar. Kullanım alanı, akustik, akışkanlar mekaniği ve elektromanyetikte oldukça fazladır. Denklemin dalga hareketinde bulunan herhangi bir u skaler büyüklüğü için gösterimleri
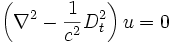
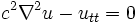
Gösterim Açıklama operatörü : u'nun zamana göre 2. türevi : d'Alembert İşlemcisi Burada c dalganın yayılma veya ilerleme hızıdır. Dalganın dağılması, yani ilerledikçe başka başka frekanslar haline bürünmesi olgusu (dispersion) göz önüne alınırsa denklemde c yerine faz hızı kullanılır. Ayrıca daha gerçekçi sistemlerde hızın, dalganın genliğine bağlı olduğu dikkate alındığından denklem doğrusal olmayan

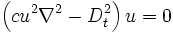
şeklinde biçimlenir.

Tek boyutta çözümü

Laplasyen tek boyutta adi türeve dönüşür.

d'Alembert çözümü

ve tanımları yapılarak zincir kuralı yardımıyla:
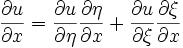
yazılabilir.
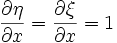
olduğundan,
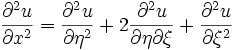
ifadesi ve aynı yol izlenerek
ifadesi elde edilebilir. İki denklem birbirinden çıkartılarak dalga denklemi buradan,
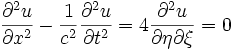
olarak yazılır. Dolayısıyla denklem,
durumuna indirgenmiş olur. Kısmî diferansiyel denklemin çözümü, tek tek değişkenler için integral alınarak
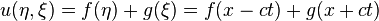
olarak bulunur. Burada f, +x yönünde ilerleyen, g de -x yönünde ilerleyen düzlem dalgayı betimler.

Fourier dönüşümü ile

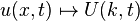
Denklem yazılıp iki tarafa da Fourier dönüşümü yapılırsa
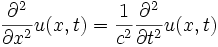
biçimine dönüşür.
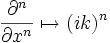
denkliği kullanılarak
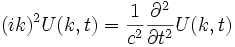
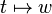
diferansiyel denklemi elde edilir. Burada, dönüşümü de uygulanarak dalga denkleminin w,k uzayındaki dağılım (dispersion) ilişkisini vermesi görülebilir. Elde edilmiş olan diferansiyel denklemin çözümü
olarak elde edilir. Ancak bu çözüm konum uzayı x de değil, başka bir uzay olan k uzayındaki çözümdür. Çözümün konum uzayında bulunabilmesi için k uzayındaki çözüme ters Fourier dönüşümü uygulanır.
çözülüerek
Görüldüğü üzere birinci ve ikinci terim sırasıyla f ve g diye iki fonksiyonun Fourier dönüşümleri olarak kabul edilirse x uzayındaki çözüm
olarak elde edilir.

Değişkenlere ayırma yöntemi ile

Dalga denklemi karışık türevler içermediği için değişkenlere ayırma yöntemi kullanılarak da çözüme gidilebilir.
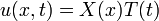
olarak yazılır ve denkleme konulursa denklem şu hali alır:
iki taraf da u ya bölünürse
iki tane birbirinden bağımsız değişkenin olduğu ifade birbirine ancak bir sabite eşit olmaları durumunda eşit olabileceğinden iki denklem de ayrı ayrı bu sabite eşitlenerek çözümler bulunabilir. Bu sabit pozitif, negatif ve sıfır olması durumlarında incelenerek diferansiyel denklemler çözülebilir ancak fizikte zaman genelde salınım olarak ortaya çıktığından sabit, − k2, k:reel seçilerek fiziksel olarak anlamlı çözüme hızlıca gidilebilir. Böylece denklemin sol tarafından:
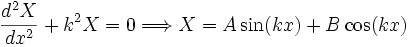
ve sağ tarafından da
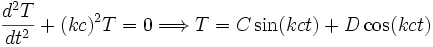
bulunur. Sinüs ve kosinüs ile elde edilen çözümler sınır koşullarını rahatça sağlayacaklarından genellikle sınır değer problemlerinde kullanılırlar. Dalga boşlukta hareket eden bir elektromanyetik bir ışınsa o zaman çözümleri K1eikx ve K2eikct olarak vermek daha rahat olur. Matematiksel olarak iki çözüm de doğru olmasına rağmen fiziksel kaidelerden serbest ve bağlı olarak çözümler böyle sınıflandırılabilir.

Dirac denklemi



Adını İngiliz fizikçi Paul Dirac'tan alan dönülü ve göreli kuantum mekaniği denklemi,
şeklinde ifade edilebilir. Burada;
m_0 : parçacığın durağan kütlesini,c : ışık hızını,pμ : dörtmomentumu,γμ : Dirac matrislerini göstermektedir. Ayrıca Ψ, dört tane karmaşık sayıdan oluşan bir kolon matristir ve olasılığın dalga fonksiyonudur. Bu dört sayı da iki gruba ayrılır:
Buradaki Ψ + ve Ψ − , Dirac dönücüleri olarak adlandırılır ve her birinin farklı bir fiziksel anlamı vardır. Ψ + dönücüsü, pozitif enerjileri, Ψ − negatif enerjileri ifāde eder. Bunlar da
ve olarak tanımlanır. ψ yukarı dönü ve φ aşağı dönü olarak anlam kazanır. Yani, dalga fonksiyonu;
şeklindedir.

Serbest parçacık için Dirac denklemi

Dırac denklemlerinde μ = 0 bileşenini ayırıp gerisi için i=1,2,3 indisini bırakırsak (bknz. Minkowski uzayzamanı), Dirac denklemi;
biçiminde yazılabilir. Dirac matrisleri; I, birim matris olmak üzere
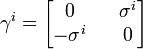
ve olarak Pauli matrisleri cinsinden yazılabilir. Bunlar yerine konunca Dirac denklemi,
biçimini alır. Matris çarpımı yapılırsa, çiftlenimli denklemler elde edilir:
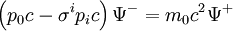
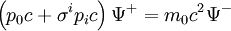
Bu özdeğer denklemlerini çözmek için, dönücülerden biri çekilip diğer denklemde yerine yazılabilir. Buradan, göreliliğin en önemli denklemlerinden biri elde edilir:
Burada p0c = E = mc2 ve olduğundan ifade,
şeklindedir. Buradan E için pozitif ve negatif değerler gelir.

Elektromanyetik alanda Dirac denklemi

Denklemdeki dörtmomentum işlemcisine elektromanyetik potansiyeli dahil edersek:
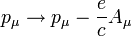
denklem,
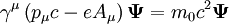
biçimine gelir. Buradaki Aμ, elektromanyetik dörtpotansiyeldir ve e elektriksel yüktür.

Doğrusal denklem
Doğrusal (Lineer) Denklem terimlerinin her biri ya birinci dereceden değişken ya da bir sabit olan denklemlerdir. Bu tür denklemler aynı zamanda birinci dereceden bir polinom belirtirler. Böyle denklemlere "doğrusal" denmesinin nedeni içerdikleri terim ve değişkenlerin sayısına bağlı olarak (n) düzlemde ya da uzayda (ya da n-boyutlu ortam) bir doğru belirtmesindendir. Doğrusal denklemlerin en yaygını bir x ve y değişkeni içeren aşağıdaki formdur:
Burada, m sabiti doğrunun eğimini belirler; b sabiti ise denklemin x ve y eksenlerini keseceği noktaları belirler (yani m sabiti değişmesi fonksiyonun artış miktarını etkilerken b sabitinin değişmesi doğrunun düzlemde ötelenmesine neden olur). Aynı terimde iki değişken barındıran ya da değişken terimin derecesi 1'den farklı olan denklemler: x2 ya da y1 / 3 (terimler birinci dereceden ya da bir sabit olmadığından) ve xy (tek bir terim çift değişken içerdiğinden) doğrusal değildir.

Örnekler
İki değişkenli bazı doğrusal denklem örnekleri:

İki Boyutlu Doğrusal Denklemler


Aşağıdaki formlar basit matematik bilgisiyle yazılabilecek 2 boyutlu doğrusal denklem örnekleridir. Burada büyük harfler sabitlerin x ve y'ler değişkenlerin yerine kullanılmıştır.

• Genel form

Hem A hem B'nin sıfıra eşit olmadığı durumalrda denklem genelde A ≥ 0 olacak şekilde yazılır. Denklemin grafiği bir doğru belirtir. A sıfır olmadıkça denklem x eksenini değeri -C/A olan bir a noktasında keser, B sıfır olmadıkça denklem y eksenini değeri -C/B olan bir b noktasında keser. A/B ise denklemin eğimini (m'yi) verir.

• Standart form

A ve B sıfır olmadıkça A, B, ve C en büyük ortak çarpanı 1 olan tamsayılardan seçilir. Genelde A ≥ 0'dir. A sıfır olmadıkça denklem x eksenini değeri C/A olan bir a noktasında keser, B sıfır olmadıkça denklem y eksenini değeri C/B olan bir b noktasında keser. A/B ise denklemin eğimini (m'yi) verir.

• Eğim-kesim noktası formu

Kesim noktası: Doğrunun herhangi bir eksenle kesiştiği noktadır. Örneğin sağdaki grafikte (a,0) x ekseni kesim noktası; (0,b) y ekseni kesim noktasıdır.

m eğimi ve b de y-ekseni kesim noktasını gösterir. x = 0 de y = b olduğu direk gözlenir.

• Nokta-eğim formu

m eğim ve (x1,y1) doğru üzerinde herhangi bir noktadır. Bazen nokta-eğim formü şu şekilde de karşımıza çıkabilir: Ancak, bu şekilde x = x1 durumunda eşitlik sağlanmaz.

• Kesim noktası formu

E ve F sıfırdan farklı olmalıdır. Doğru ve x ekseninin kesiştiği nokta (x ekseninin kesim noktası) E ve y ekseninin kesim noktası F'dir. A = 1/E, B = 1/F ve C = 1 alınarak kolaylıkla standart forma dönüştürülebilir.

• İki nokta formu

p ≠ h. Grafik (h,k)'ya karşılık (p,q) noktasını sağlar ve eğim m = (q−k) / (p−h)'dir.

• Parametrik form

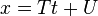
ve olsun şeklinde iki denklemdir. eğim m = V / T, x-kesim noktası a=(VU−WT) / V ve y-kesim noktası b=(WT−VU) / T

• Normal form

φ normalin eğim açısı ve p de normalin uzunluğudur. Normal doğru ve başlangıç noktası (orijin) arasında doğruya dik olacak en kısa doğru parçasıdır. Tüm katsayılar by 'a bölünerek ve eğer C > 0'sa tüm katsayılar -1'le çarpılarak (böylece son katsayı negatif olur) rahatça bulunabilir. Alman Matematikçi Ludwig Otto Hesse'nin anısına bu form ayrıca Hesse standart formu olarak da anılır. Bazen denklemlerde sadeleştirme işlemlerinden sonra eşitsizlik söz konusu olabilir, 1 = 0 gibi. Bu gibi eşitsizlikler tutarsız eşitsizliklerdir, yani hiç bir x ve y değeri için doğru değildir. 3x + 2 = 3x − 5 buna örnek olabilir.
Birden fazla doğrusal denklem olduğu durumlar için lütfen bkz.: Doğrusal denklem sistemi.

Doğrusal fonksiyonlarla ilişkisi
Yukarıdaki tüm formlarda y, x'in bir fonksiyonudur. Fonksiyon grafiği denklem grafiğiyle aynıdır.
Denklemdeki y = f(x) varsayılırsa f fonksiyonu aşağıdaki özelliklere sahiptir:
ve
a bir sayıdır. Bunları sağlayan fonksiyonlara doğrusal fonksiyon denir.

İkiden fazla değişkenli doğrusal denklemler
Doğrusal denklemler ikiden fazla değişkene de sahip olabilirler, n terimli genel denklemimiz aşağıdaki gibi olsun:
Burada, a1, a2, …, an katsayılar, x1, x2, …, xn değişkenlerdir, ve b de sabittir. Üç değişkenli denklemlerde genelde x1 yerine sadece x, x2 sadece y ve x3 yerine z kullanılır.
Böyle bir denklem n-boyutlu bir Öklid uzayında (n–1)-boyutlu hiper düzlem belirtir.