Helmholtz denklemi

Hermann von Helmholtz'un ardından adlandirilan Helmholtz denklemi veya indirgenmiş dalga denklemi


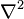
biciminde tanimli 2. dereceden bir eliptik kismi türevli diferansiyel denklemdir. Burada (Δ biciminde de gosterilir) Laplasyen operatörünü, k(x) ortamın dalga sayısını ve u(x) dalga davranışı gösteren bilinmeyen fonksiyonu göstermektedir.

Homojen olmayan Helmholtz denklemi


Bu durumda denklem fiziksel acidan u(.) alaninin f(.) kaynak dagilimi tarafindan yaratildigi biciminde yorumlanir.

Uygulama Alanları

Helmholtz denklemi zamanla harmonik degisim gosteren elektromagnetik veya akustik dalgalarla uyarılmış ortamlardaki alan dagılımını modellemek için kullanılır.

Laplace denklemi



Matematikte Laplace denklemi, özellikleri ilk defa Pierre-Simon Laplace tarafından çalışılmış bir kısmi diferansiyel denklemdir. Laplace denkleminin çözümleri, elektromanyetizma, astronomi ve akışkanlar dinamiği gibi birçok bilim alanında önemlidir çünkü çözümler bilhassa elektrik ve yerçekim potansiyeli ile akışkan potansiyelinin davranışını açıklar. Laplace denkleminin çözümlerinin genel teorisi aynı zamanda potansiyel teorisi olarak da bilinmektedir.
Tanım

Üç boyutta, problem x, y ve z gibi üç gerçel değişkene sahip, iki kere türevlenebilir, gerçel değerli ve
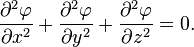
denklemini sağlayan bir fonksiyonu bulmaktır.
Çoğunlukla bu denklem
denklemi olarak veya div'in diverjansı ve grad'ın ise gradyanı temsil ettiği
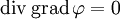
denklemi olarak veya Δ'nın Laplace operatörü olduğu
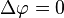
denklemi olarak yazılır.
Laplace denkleminin çözümlerine aynı zamanda harmonik fonksiyonlar da denmektedir.
Denklemin sağ tarafı eğer belli bir f(x, y, z) fonksiyonu şeklinde verilirse, yani denklem
olarak ifade edilirse, o zaman denkleme "Poisson denklemi" adı verilir.
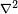
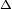
Laplace ve Poisson denklemleri eliptik kısmi diferansiyel denklemlerin en basit örnekleridir. Kısmi diferansiyel operatörü olan ve herhangi bir boyutta tanımlanabilen 'ye veya 'ya Laplace operatörü veya kısaca Laplasyen denmektedir.

Sınır koşulları

Laplace denklemi için Dirichlet problemi bir D bölgesi üzerinde tanımlı ve verilmiş başka bir fonksiyona D 'nin sınırı üzerinde eşit olan bir fonksiyonu bulmaktan ibarettir. Laplace operatörü ısı denkleminde yer aldığı için, problemin bir diğer yorumu da şöyledir: Bölgenin sınırındaki sıcaklık sabit tutulur ve bölgenin iç tarafındaki sıcaklık artık değişmeyecek şekilde beklenilir. İç bölgedeki sıcaklık dağılımı artık ilişkin Dirichlet probleminin çözümü tarafından verilecektir.
Laplace denklemi için Neumann sınır koşulları D'nin sınırında fonsiyonunu belirtmez ancak bu fonksiyonun normal türevini belirtir. Fiziksel olarak bu durum, yalnız D'nin sınırında etkisi bilinen bir vektör alanı için olan bir potansiyelin inşasına (oluşturulmasına) denk gelmektedir.
Laplace denkleminin çözümlerine harmonik fonksiyonlar denilmektedir ve bu fonksiyonların hepsi denklemin sağlandığı bölge içinde analitiktir. Eğer iki fonksiyon Laplace denkleminin (veya herhangi doğrusal homojen diferansiyel denklemin) çözümüyse, toplamları (veya herhangi doğrusal kombinasyonları) da ayrıca bir çözümdür. Süperpozisyon ilkesi de denilen bu özellik özellikle karmaşık problemlerin basit çözümlerin toplanılması yoluyla yapılan çözümlerinde çok yararlıdır.

İki boyutta Laplace denklemi

İki değişkenli Laplace denklemi
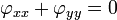
formuna sahiptir.



Analitik fonksiyonlar

Karmaşık analitik bir fonksiyonun gerçel ve sanal kısmının her ikisi de Laplace denklemini sağlar. Eğer z=x+iy ise ve
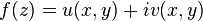
ise, o zaman f(z) 'nin analitik olması için gerekli koşul aşağıdaki Cauchy-Riemann denklemlerinin sağlanmasıdır:
Takip eden ifade ise
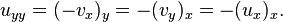
olacaktır. Bu yüzden u Laplace denklemini sağlar. Benzer bir hesaplama yine v 'nin de Laplace denklemini sağladığını gösterir.
Aksine diğer taraftan bir harmonik fonksiyon verilirse, bu fonksiyon analitik bir f(z) fonksiyonunun gerçel kısmı olur (en azından yerel olarak). Eğer
olarak alınırsa ve
şartı konulursa, o zaman Cauchy-Riemann denklemleri sağlanacaktır.
Bu ilişki ψ'yi belirlemese de artışlarını belirler:
φ için Laplace denklemi ψ'nin integrallenebilme koşulunun sağlandığını gösterir:
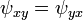
ve bu yüzden ψ bir çizgi integrali yoluyla tanımlanabilir. İntegrallenebilme koşulu ve Stoke teoremi iki noktayı birleştiren çizgi integralinin değerinin takip edilen yoldan bağımsız olduğunu gösterir. Laplace denkleminin sonucunda çıkan çözüm çiftine eşlenik harmonik fonksiyonlar adı verilir. Bu inşa sadece yerel olarak veya takip edilen yolun bir tekilliği çevrelememesi koşuluyla geçerlidir. Örneğin, r ve θ kutupsal koordinatlar olursa ve
ise, o zaman karşılık gelen analitik fonksiyon
fonksiyonudur. Bununla birlikte, θ açısı orijini çevrelemeyen bir bölge içinde tek (bir) değerlidir.
Laplace denklemi ve analitik fonksiyonlar arasındaki yakın ilişki Laplace denkleminin çözümünün her mertebeden türevi olduğunu gösterir ve bu çözüm en azından bir tekilliği çevrelemeyen bir çember içinde kuvvet serilerine genişletilebilir. Bu durum, daha az düzenliliğe sahip ısı denklemi çözümleriyle tezat bir haldedir.
Kuvvet serileri ve Fourier serileri arasında sıkı bir ilişki vardır. Bir f fonksiyonu R yarıçaplı bir çember içinde kuvvet serisine genişletilirse, bu gerçel ve sanal kısımları
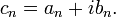
şeklinde olan uygun katsayıların olduğu
ifadesi anlamına gelir. Bu yüzden,
olur ki bu da f 'nin Fourier seridir.

Akışkan akımı

u ve v nicelikleri durağan sıkıştırılamaz, dönmez bir akımın iki boyutta yatay ve dikey bileşenleri olsun. Akımın sıkıştırılamaz olmasının koşulu,
olmasıdır ve akımın dönmez olmasının şartı da
olmasıdır. Bir ψ fonksiyonunun diferansiyeli
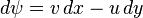
olarak tanımlanırsa, o zaman sıkıştırılamama şartı bu diferansiyel için integrallenebilme koşulu olur: Sonuçtaki fonksiyona akış fonksiyonu adı verilir çünkü bu fonksiyon akım çizgileri boyunca sabittir. ψ'nin birinci türevi
ile verilir ve sıkıştırılamama şartı ψ 'nin Laplace denklemini sağladığını gösterir. ψ 'ye eşlenik olan harmonik φ fonksiyonuna hız potansiyeli denilir. Cauchy-Riemann denklemleri
ifadesini verir.
Bu yüzden her analitik fonksiyon düzlemde durağan sıkıştırılamaz, dönmez bir akışkan akıma karşılık gelir. Gerçel kısım hız potansiyeli olurken sanal kısım akış fonksiyonu olur.

Elektrostatik

Maxwell denklemleri'ne göre, iki uzay boyutunda yer alan ve zamandan bağımsız olan bir elektrik alanı (u,v),
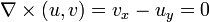
ifadesini ve ρ'nun yük yoğunluğu olduğu
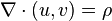
ifadesini sağlar.
Birinci Maxwell denklemi
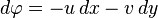
diferansiyeli için integrallenebilme koşuludur. Böylece elektrik potansiyeli olan φ
ifadesini sağlayacak şekilde inşa edilebilir.
İkinci Maxwell denklemi o zaman Poisson denklemi olarak ifade edilen
denklemini verir.
İki boyutta kullanılana benzer olarak, Laplace denklemi elektrostatik ve akışkan akımının üç boyutlu problemlerinde de kullanılabilir.

Üç boyutta Laplace denklemi


Temel çözüm

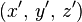
Laplace denkleminin temel çözümü, Dirac delta fonksiyonu δ'nın noktasında toplanmış bir birim kaynağı gösterdiği
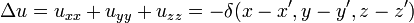
denklemini sağlar. Hiçbir fonksiyon bu özelliğe sahip değildir ancak yine de bu, integralleri uzay üzerinde birlik olan ve desteği (fonksiyonun sıfır olmadığı bölge) bir noktaya küçülen bir fonksiyonlar limiti olarak düşünülebilir. Temel çözümün tanımı bu yüzden, u 'nun Laplasyeninin kaynak noktasını çevreleyen herhengi bir hacim üzerinde integrali alındığında, o zaman
olduğunu gösterir.
Laplace denklemi koordinatların rotasyonuyla değişmez kalır ve bu yüzden bir temel çözümün, sadece (kaynak noktasından uzaklığı gösteren) r 'ye bağımlı olan çözümler arasından elde edilebileceği beklenir. Hacim kaynak noktası etrafında a yarıçaplı bir top olarak düşünülürse, o zaman Gauss diverjans teoremi
ifadesini verir. O zaman takip eden ifade ise, kaynak noktası etrafında r yarıçaplı bir küre üzerindeki
ifadesidir ve bu yüzden
olur. Benzer bir hesap ise iki boyutta
olduğunu gösterir.

Green fonksiyonu

Bir Green fonksiyonu da bir V hacminin S sınırındaki uygun şartı sağlayan temel bir çözümdür. Örneğin, ,
ifadelerini sağlayabilir.
Eğer u, V üzerinde Poisson denkleminin herhangi bir çözümüyse
olur ve u, S üzerinde g sınır değerlerini alır. O zaman aşağıdaki eşitlikleri veren (diverjans teoreminin bir sonucu olan) Green özdeşliğine başvurulabilir:
un ve Gn gösterimleri S üzerindeki normal türevleri ifade etmektedir. u ve G 'nin sağladığı şartlar bağlamında, bu sonuç
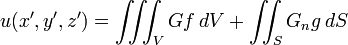
haline gelir.
Bu yüzden, Green fonksiyonu f ve g 'nin noktalarındaki etkisini açıklar. a yarıçaplı kürenin içi düşünüldüğünde ise, Green fonksiyonu yansıtma yoluyla elde edilebilir (Sommerfeld, 1949): Kürenin merkezinden ρ kadar uzaklıkta olan P kaynak noktası,
uzaklıkta bulunan bir N noktasına yarıçapsal doğru boyunca yansıtılır.
Unutulmaması gereken nokta P küre içindeyse, N 'nin küre dışında olması gerektiğidir. O zaman Green fonksiyonu R 'nin P kaynak noktasına uzaklığı ve T 'nin yansıtılmış N noktasına olan uzaklığı gösterdiği
ifadesi tarafından verilir. Green fonksiyonu için olan bu ifadenin bir sonucu ise Poisson integral formülüdür. ρ, θ, ve φ, P kaynak noktası için küresel koordinatlar olsun. Burada θ dikey eksenle olan açıyı göstermektedir. (Amerikan matematik gösterimine uymaz ancak standard Avrupa ve fiziksel uygulamalarına uyum gösteren bir gösterimdir) O zaman, küre içindeki Laplace denkleminin çözümü
olarak alınırsa
tarafından verilir.
Bu formülün basit bir sonucu ise şudur: u harmonikse, o zaman u 'nun kürenin merkezindeki değerleri, u 'nun küre üzerindeki değerlerinin ortalama değerleridir. Bu ortalama değer özelliği ise ivedilikle sabit olmayan bir fonksiyonun maksimum değerini kürenin içinde alamayacağı sonucunu verir.

Laplace denklemi



Matematikte Laplace denklemi, özellikleri ilk defa Pierre-Simon Laplace tarafından çalışılmış bir kısmi diferansiyel denklemdir. Laplace denkleminin çözümleri, elektromanyetizma, astronomi ve akışkanlar dinamiği gibi birçok bilim alanında önemlidir çünkü çözümler bilhassa elektrik ve yerçekim potansiyeli ile akışkan potansiyelinin davranışını açıklar. Laplace denkleminin çözümlerinin genel teorisi aynı zamanda potansiyel teorisi olarak da bilinmektedir.
Tanım

Üç boyutta, problem x, y ve z gibi üç gerçel değişkene sahip, iki kere türevlenebilir, gerçel değerli ve
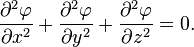
denklemini sağlayan bir fonksiyonu bulmaktır.
Çoğunlukla bu denklem
denklemi olarak veya div'in diverjansı ve grad'ın ise gradyanı temsil ettiği
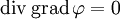
denklemi olarak veya Δ'nın Laplace operatörü olduğu
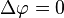
denklemi olarak yazılır.
Laplace denkleminin çözümlerine aynı zamanda harmonik fonksiyonlar da denmektedir.
Denklemin sağ tarafı eğer belli bir f(x, y, z) fonksiyonu şeklinde verilirse, yani denklem
olarak ifade edilirse, o zaman denkleme "Poisson denklemi" adı verilir.
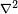
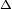
Laplace ve Poisson denklemleri eliptik kısmi diferansiyel denklemlerin en basit örnekleridir. Kısmi diferansiyel operatörü olan ve herhangi bir boyutta tanımlanabilen 'ye veya 'ya Laplace operatörü veya kısaca Laplasyen denmektedir.

Sınır koşulları

Laplace denklemi için Dirichlet problemi bir D bölgesi üzerinde tanımlı ve verilmiş başka bir fonksiyona D 'nin sınırı üzerinde eşit olan bir fonksiyonu bulmaktan ibarettir. Laplace operatörü ısı denkleminde yer aldığı için, problemin bir diğer yorumu da şöyledir: Bölgenin sınırındaki sıcaklık sabit tutulur ve bölgenin iç tarafındaki sıcaklık artık değişmeyecek şekilde beklenilir. İç bölgedeki sıcaklık dağılımı artık ilişkin Dirichlet probleminin çözümü tarafından verilecektir.
Laplace denklemi için Neumann sınır koşulları D'nin sınırında fonsiyonunu belirtmez ancak bu fonksiyonun normal türevini belirtir. Fiziksel olarak bu durum, yalnız D'nin sınırında etkisi bilinen bir vektör alanı için olan bir potansiyelin inşasına (oluşturulmasına) denk gelmektedir.
Laplace denkleminin çözümlerine harmonik fonksiyonlar denilmektedir ve bu fonksiyonların hepsi denklemin sağlandığı bölge içinde analitiktir. Eğer iki fonksiyon Laplace denkleminin (veya herhangi doğrusal homojen diferansiyel denklemin) çözümüyse, toplamları (veya herhangi doğrusal kombinasyonları) da ayrıca bir çözümdür. Süperpozisyon ilkesi de denilen bu özellik özellikle karmaşık problemlerin basit çözümlerin toplanılması yoluyla yapılan çözümlerinde çok yararlıdır.

İki boyutta Laplace denklemi

İki değişkenli Laplace denklemi
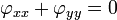
formuna sahiptir.



Analitik fonksiyonlar

Karmaşık analitik bir fonksiyonun gerçel ve sanal kısmının her ikisi de Laplace denklemini sağlar. Eğer z=x+iy ise ve
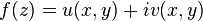
ise, o zaman f(z) 'nin analitik olması için gerekli koşul aşağıdaki Cauchy-Riemann denklemlerinin sağlanmasıdır:
Takip eden ifade ise
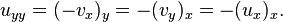
olacaktır. Bu yüzden u Laplace denklemini sağlar. Benzer bir hesaplama yine v 'nin de Laplace denklemini sağladığını gösterir.
Aksine diğer taraftan bir harmonik fonksiyon verilirse, bu fonksiyon analitik bir f(z) fonksiyonunun gerçel kısmı olur (en azından yerel olarak). Eğer
olarak alınırsa ve
şartı konulursa, o zaman Cauchy-Riemann denklemleri sağlanacaktır.
Bu ilişki ψ'yi belirlemese de artışlarını belirler:
φ için Laplace denklemi ψ'nin integrallenebilme koşulunun sağlandığını gösterir:
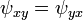
ve bu yüzden ψ bir çizgi integrali yoluyla tanımlanabilir. İntegrallenebilme koşulu ve Stoke teoremi iki noktayı birleştiren çizgi integralinin değerinin takip edilen yoldan bağımsız olduğunu gösterir. Laplace denkleminin sonucunda çıkan çözüm çiftine eşlenik harmonik fonksiyonlar adı verilir. Bu inşa sadece yerel olarak veya takip edilen yolun bir tekilliği çevrelememesi koşuluyla geçerlidir. Örneğin, r ve θ kutupsal koordinatlar olursa ve
ise, o zaman karşılık gelen analitik fonksiyon
fonksiyonudur. Bununla birlikte, θ açısı orijini çevrelemeyen bir bölge içinde tek (bir) değerlidir.
Laplace denklemi ve analitik fonksiyonlar arasındaki yakın ilişki Laplace denkleminin çözümünün her mertebeden türevi olduğunu gösterir ve bu çözüm en azından bir tekilliği çevrelemeyen bir çember içinde kuvvet serilerine genişletilebilir. Bu durum, daha az düzenliliğe sahip ısı denklemi çözümleriyle tezat bir haldedir.
Kuvvet serileri ve Fourier serileri arasında sıkı bir ilişki vardır. Bir f fonksiyonu R yarıçaplı bir çember içinde kuvvet serisine genişletilirse, bu gerçel ve sanal kısımları
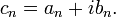
şeklinde olan uygun katsayıların olduğu
ifadesi anlamına gelir. Bu yüzden,
olur ki bu da f 'nin Fourier seridir.

Akışkan akımı

u ve v nicelikleri durağan sıkıştırılamaz, dönmez bir akımın iki boyutta yatay ve dikey bileşenleri olsun. Akımın sıkıştırılamaz olmasının koşulu,
olmasıdır ve akımın dönmez olmasının şartı da
olmasıdır. Bir ψ fonksiyonunun diferansiyeli
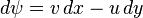
olarak tanımlanırsa, o zaman sıkıştırılamama şartı bu diferansiyel için integrallenebilme koşulu olur: Sonuçtaki fonksiyona akış fonksiyonu adı verilir çünkü bu fonksiyon akım çizgileri boyunca sabittir. ψ'nin birinci türevi
ile verilir ve sıkıştırılamama şartı ψ 'nin Laplace denklemini sağladığını gösterir. ψ 'ye eşlenik olan harmonik φ fonksiyonuna hız potansiyeli denilir. Cauchy-Riemann denklemleri
ifadesini verir.
Bu yüzden her analitik fonksiyon düzlemde durağan sıkıştırılamaz, dönmez bir akışkan akıma karşılık gelir. Gerçel kısım hız potansiyeli olurken sanal kısım akış fonksiyonu olur.

Elektrostatik

Maxwell denklemleri'ne göre, iki uzay boyutunda yer alan ve zamandan bağımsız olan bir elektrik alanı (u,v),
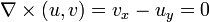
ifadesini ve ρ'nun yük yoğunluğu olduğu
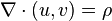
ifadesini sağlar.
Birinci Maxwell denklemi
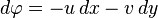
diferansiyeli için integrallenebilme koşuludur. Böylece elektrik potansiyeli olan φ
ifadesini sağlayacak şekilde inşa edilebilir.
İkinci Maxwell denklemi o zaman Poisson denklemi olarak ifade edilen
denklemini verir.
İki boyutta kullanılana benzer olarak, Laplace denklemi elektrostatik ve akışkan akımının üç boyutlu problemlerinde de kullanılabilir.

Üç boyutta Laplace denklemi


Temel çözüm

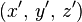
Laplace denkleminin temel çözümü, Dirac delta fonksiyonu δ'nın noktasında toplanmış bir birim kaynağı gösterdiği
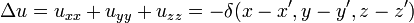
denklemini sağlar. Hiçbir fonksiyon bu özelliğe sahip değildir ancak yine de bu, integralleri uzay üzerinde birlik olan ve desteği (fonksiyonun sıfır olmadığı bölge) bir noktaya küçülen bir fonksiyonlar limiti olarak düşünülebilir. Temel çözümün tanımı bu yüzden, u 'nun Laplasyeninin kaynak noktasını çevreleyen herhengi bir hacim üzerinde integrali alındığında, o zaman
olduğunu gösterir.
Laplace denklemi koordinatların rotasyonuyla değişmez kalır ve bu yüzden bir temel çözümün, sadece (kaynak noktasından uzaklığı gösteren) r 'ye bağımlı olan çözümler arasından elde edilebileceği beklenir. Hacim kaynak noktası etrafında a yarıçaplı bir top olarak düşünülürse, o zaman Gauss diverjans teoremi
ifadesini verir. O zaman takip eden ifade ise, kaynak noktası etrafında r yarıçaplı bir küre üzerindeki
ifadesidir ve bu yüzden
olur. Benzer bir hesap ise iki boyutta
olduğunu gösterir.

Green fonksiyonu

Bir Green fonksiyonu da bir V hacminin S sınırındaki uygun şartı sağlayan temel bir çözümdür. Örneğin, ,
ifadelerini sağlayabilir.
Eğer u, V üzerinde Poisson denkleminin herhangi bir çözümüyse
olur ve u, S üzerinde g sınır değerlerini alır. O zaman aşağıdaki eşitlikleri veren (diverjans teoreminin bir sonucu olan) Green özdeşliğine başvurulabilir:
un ve Gn gösterimleri S üzerindeki normal türevleri ifade etmektedir. u ve G 'nin sağladığı şartlar bağlamında, bu sonuç
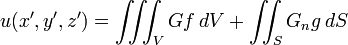
haline gelir.
Bu yüzden, Green fonksiyonu f ve g 'nin noktalarındaki etkisini açıklar. a yarıçaplı kürenin içi düşünüldüğünde ise, Green fonksiyonu yansıtma yoluyla elde edilebilir (Sommerfeld, 1949): Kürenin merkezinden ρ kadar uzaklıkta olan P kaynak noktası,
uzaklıkta bulunan bir N noktasına yarıçapsal doğru boyunca yansıtılır.
Unutulmaması gereken nokta P küre içindeyse, N 'nin küre dışında olması gerektiğidir. O zaman Green fonksiyonu R 'nin P kaynak noktasına uzaklığı ve T 'nin yansıtılmış N noktasına olan uzaklığı gösterdiği
ifadesi tarafından verilir. Green fonksiyonu için olan bu ifadenin bir sonucu ise Poisson integral formülüdür. ρ, θ, ve φ, P kaynak noktası için küresel koordinatlar olsun. Burada θ dikey eksenle olan açıyı göstermektedir. (Amerikan matematik gösterimine uymaz ancak standard Avrupa ve fiziksel uygulamalarına uyum gösteren bir gösterimdir) O zaman, küre içindeki Laplace denkleminin çözümü
olarak alınırsa
tarafından verilir.
Bu formülün basit bir sonucu ise şudur: u harmonikse, o zaman u 'nun kürenin merkezindeki değerleri, u 'nun küre üzerindeki değerlerinin ortalama değerleridir. Bu ortalama değer özelliği ise ivedilikle sabit olmayan bir fonksiyonun maksimum değerini kürenin içinde alamayacağı sonucunu verir.