Helmholtz denklemi Hermann von Helmholtz'un ardından adlandirilan
Helmholtz denklemi veya
indirgenmiş dalga denklemi 
biciminde tanimli 2. dereceden bir eliptik kismi türevli diferansiyel denklemdir. Burada
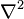
(Δ biciminde de gosterilir)
Laplasyen operatörünü,
k(
x) ortamın dalga sayısını ve
u(
x) dalga davranışı gösteren bilinmeyen fonksiyonu göstermektedir.
Homojen olmayan Helmholtz denklemi 
Bu durumda denklem fiziksel acidan u(.) alaninin f(.) kaynak dagilimi tarafindan yaratildigi biciminde yorumlanir.
Uygulama Alanları
Helmholtz denklemi zamanla harmonik degisim gosteren elektromagnetik veya akustik dalgalarla uyarılmış ortamlardaki alan dagılımını modellemek için kullanılır.
Laplace denklemi Matematikte Laplace denklemi, özellikleri ilk defa
Pierre-Simon Laplace tarafından çalışılmış bir
kısmi diferansiyel denklemdir. Laplace denkleminin çözümleri, elektromanyetizma, astronomi ve akışkanlar dinamiği gibi birçok bilim alanında önemlidir çünkü çözümler bilhassa elektrik ve yerçekim
potansiyeli ile akışkan potansiyelinin davranışını açıklar. Laplace denkleminin çözümlerinin genel teorisi aynı zamanda
potansiyel teorisi olarak da bilinmektedir.
Tanım
Üç boyutta, problem
x,
y ve
z gibi üç gerçel değişkene sahip, iki kere
türevlenebilir, gerçel değerli ve
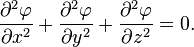
denklemini sağlayan bir

fonksiyonu bulmaktır.
Çoğunlukla bu denklem

denklemi olarak veya div'in
diverjansı ve grad'ın ise
gradyanı temsil ettiği
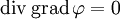
denklemi olarak veya Δ'nın
Laplace operatörü olduğu
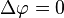
denklemi olarak yazılır.
Laplace denkleminin çözümlerine aynı zamanda
harmonik fonksiyonlar da denmektedir.
Denklemin sağ tarafı eğer belli bir
f(
x,
y,
z) fonksiyonu şeklinde verilirse, yani denklem

olarak ifade edilirse, o zaman denkleme "
Poisson denklemi" adı verilir.
Laplace ve Poisson denklemleri
eliptik kısmi diferansiyel denklemlerin en basit örnekleridir. Kısmi diferansiyel operatörü olan ve herhangi bir boyutta tanımlanabilen
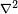
'ye veya
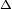
'ya
Laplace operatörü veya kısaca
Laplasyen denmektedir.
Sınır koşulları
Laplace denklemi için
Dirichlet problemi bir
D bölgesi üzerinde tanımlı ve verilmiş başka bir fonksiyona
D 'nin sınırı üzerinde eşit olan bir

fonksiyonu bulmaktan ibarettir. Laplace operatörü
ısı denkleminde yer aldığı için, problemin bir diğer yorumu da şöyledir: Bölgenin sınırındaki sıcaklık sabit tutulur ve bölgenin iç tarafındaki sıcaklık artık değişmeyecek şekilde beklenilir. İç bölgedeki sıcaklık dağılımı artık ilişkin Dirichlet probleminin çözümü tarafından verilecektir.
Laplace denklemi için
Neumann sınır koşulları D'nin sınırında

fonsiyonunu belirtmez ancak bu fonksiyonun normal türevini belirtir. Fiziksel olarak bu durum, yalnız
D'nin sınırında etkisi bilinen bir vektör alanı için olan bir potansiyelin inşasına (oluşturulmasına) denk gelmektedir.
Laplace denkleminin çözümlerine
harmonik fonksiyonlar denilmektedir ve bu fonksiyonların hepsi denklemin sağlandığı bölge içinde
analitiktir. Eğer iki fonksiyon Laplace denkleminin (veya herhangi doğrusal homojen diferansiyel denklemin) çözümüyse, toplamları (veya herhangi doğrusal kombinasyonları) da ayrıca bir çözümdür.
Süperpozisyon ilkesi de denilen bu özellik özellikle karmaşık problemlerin basit çözümlerin toplanılması yoluyla yapılan çözümlerinde çok yararlıdır.
İki boyutta Laplace denklemi
İki değişkenli Laplace denklemi
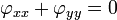
formuna sahiptir.
Analitik fonksiyonlar
Karmaşık analitik bir fonksiyonun gerçel ve sanal kısmının her ikisi de Laplace denklemini sağlar. Eğer
z=
x+
iy ise ve
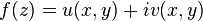
ise, o zaman
f(
z) 'nin analitik olması için gerekli koşul aşağıdaki Cauchy-Riemann denklemlerinin sağlanmasıdır:

Takip eden ifade ise
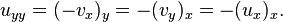
olacaktır. Bu yüzden
u Laplace denklemini sağlar. Benzer bir hesaplama yine
v 'nin de Laplace denklemini sağladığını gösterir.
Aksine diğer taraftan bir harmonik fonksiyon verilirse, bu fonksiyon analitik bir
f(
z) fonksiyonunun gerçel kısmı olur (en azından yerel olarak). Eğer

olarak alınırsa ve

şartı konulursa, o zaman Cauchy-Riemann denklemleri sağlanacaktır.
Bu ilişki ψ'yi belirlemese de artışlarını belirler:

φ için Laplace denklemi ψ'nin integrallenebilme koşulunun sağlandığını gösterir:
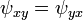
ve bu yüzden ψ bir çizgi integrali yoluyla tanımlanabilir. İntegrallenebilme koşulu ve
Stoke teoremi iki noktayı birleştiren çizgi integralinin değerinin takip edilen yoldan bağımsız olduğunu gösterir. Laplace denkleminin sonucunda çıkan çözüm çiftine
eşlenik harmonik fonksiyonlar adı verilir. Bu inşa sadece yerel olarak veya takip edilen yolun bir tekilliği çevrelememesi koşuluyla geçerlidir. Örneğin,
r ve θ kutupsal koordinatlar olursa ve

ise, o zaman karşılık gelen analitik fonksiyon

fonksiyonudur. Bununla birlikte, θ açısı orijini çevrelemeyen bir bölge içinde tek (bir) değerlidir.
Laplace denklemi ve analitik fonksiyonlar arasındaki yakın ilişki Laplace denkleminin çözümünün her mertebeden türevi olduğunu gösterir ve bu çözüm en azından bir tekilliği çevrelemeyen bir çember içinde kuvvet serilerine genişletilebilir. Bu durum, daha az düzenliliğe sahip
ısı denklemi çözümleriyle tezat bir haldedir.
Kuvvet serileri ve Fourier serileri arasında sıkı bir ilişki vardır. Bir
f fonksiyonu
R yarıçaplı bir çember içinde kuvvet serisine genişletilirse, bu gerçel ve sanal kısımları
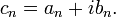
şeklinde olan uygun katsayıların olduğu

ifadesi anlamına gelir. Bu yüzden,

olur ki bu da
f 'nin Fourier seridir.
Akışkan akımı u ve
v nicelikleri durağan sıkıştırılamaz, dönmez bir akımın iki boyutta yatay ve dikey bileşenleri olsun. Akımın sıkıştırılamaz olmasının koşulu,

olmasıdır ve akımın dönmez olmasının şartı da

olmasıdır. Bir ψ fonksiyonunun diferansiyeli
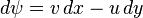
olarak tanımlanırsa, o zaman sıkıştırılamama şartı bu diferansiyel için integrallenebilme koşulu olur: Sonuçtaki fonksiyona
akış fonksiyonu adı verilir çünkü bu fonksiyon akım çizgileri boyunca sabittir. ψ'nin birinci türevi

ile verilir ve sıkıştırılamama şartı ψ 'nin Laplace denklemini sağladığını gösterir. ψ 'ye eşlenik olan harmonik φ fonksiyonuna
hız potansiyeli denilir. Cauchy-Riemann denklemleri

ifadesini verir.
Bu yüzden her analitik fonksiyon düzlemde durağan sıkıştırılamaz, dönmez bir akışkan akıma karşılık gelir. Gerçel kısım hız potansiyeli olurken sanal kısım akış fonksiyonu olur.
Elektrostatik Maxwell denklemleri'ne göre, iki uzay boyutunda yer alan ve zamandan bağımsız olan bir elektrik alanı (
u,
v),
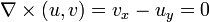
ifadesini ve ρ'nun yük yoğunluğu olduğu
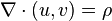
ifadesini sağlar.
Birinci Maxwell denklemi
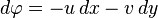
diferansiyeli için integrallenebilme koşuludur. Böylece elektrik potansiyeli olan φ

ifadesini sağlayacak şekilde inşa edilebilir.
İkinci Maxwell denklemi o zaman
Poisson denklemi olarak ifade edilen

denklemini verir.
İki boyutta kullanılana benzer olarak, Laplace denklemi elektrostatik ve akışkan akımının üç boyutlu problemlerinde de kullanılabilir.
Üç boyutta Laplace denklemi Temel çözüm
Laplace denkleminin temel çözümü, Dirac delta fonksiyonu δ'nın
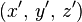
noktasında toplanmış bir birim kaynağı gösterdiği
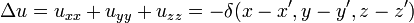
denklemini sağlar. Hiçbir fonksiyon bu özelliğe sahip değildir ancak yine de bu, integralleri uzay üzerinde birlik olan ve desteği (fonksiyonun sıfır olmadığı bölge) bir noktaya küçülen bir fonksiyonlar limiti olarak düşünülebilir. Temel çözümün tanımı bu yüzden,
u 'nun Laplasyeninin kaynak noktasını çevreleyen herhengi bir hacim üzerinde integrali alındığında, o zaman

olduğunu gösterir.
Laplace denklemi koordinatların rotasyonuyla değişmez kalır ve bu yüzden bir temel çözümün, sadece (kaynak noktasından uzaklığı gösteren)
r 'ye bağımlı olan çözümler arasından elde edilebileceği beklenir. Hacim kaynak noktası etrafında
a yarıçaplı bir top olarak düşünülürse, o zaman Gauss diverjans teoremi

ifadesini verir. O zaman takip eden ifade ise, kaynak noktası etrafında
r yarıçaplı bir küre üzerindeki

ifadesidir ve bu yüzden

olur. Benzer bir hesap ise iki boyutta

olduğunu gösterir.
Green fonksiyonu
Bir
Green fonksiyonu da bir
V hacminin
S sınırındaki uygun şartı sağlayan temel bir çözümdür. Örneğin,

,


ifadelerini sağlayabilir.
Eğer
u,
V üzerinde Poisson denkleminin herhangi bir çözümüyse

olur ve
u,
S üzerinde
g sınır değerlerini alır. O zaman aşağıdaki eşitlikleri veren (diverjans teoreminin bir sonucu olan)
Green özdeşliğine başvurulabilir:
 un
un ve
Gn gösterimleri
S üzerindeki normal türevleri ifade etmektedir.
u ve
G 'nin sağladığı şartlar bağlamında, bu sonuç
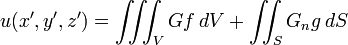
haline gelir.
Bu yüzden, Green fonksiyonu
f ve
g 'nin

noktalarındaki etkisini açıklar.
a yarıçaplı kürenin içi düşünüldüğünde ise, Green fonksiyonu yansıtma yoluyla elde edilebilir (Sommerfeld, 1949): Kürenin merkezinden ρ kadar uzaklıkta olan
P kaynak noktası,

uzaklıkta bulunan bir
N noktasına yarıçapsal doğru boyunca yansıtılır.
Unutulmaması gereken nokta
P küre içindeyse,
N 'nin küre dışında olması gerektiğidir. O zaman Green fonksiyonu
R 'nin
P kaynak noktasına uzaklığı ve
T 'nin yansıtılmış
N noktasına olan uzaklığı gösterdiği

ifadesi tarafından verilir. Green fonksiyonu için olan bu ifadenin bir sonucu ise
Poisson integral formülüdür. ρ, θ, ve φ,
P kaynak noktası için
küresel koordinatlar olsun. Burada θ dikey eksenle olan açıyı göstermektedir. (Amerikan matematik gösterimine uymaz ancak standard Avrupa ve fiziksel uygulamalarına uyum gösteren bir gösterimdir) O zaman, küre içindeki Laplace denkleminin çözümü

olarak alınırsa

tarafından verilir.
Bu formülün basit bir sonucu ise şudur:
u harmonikse, o zaman
u 'nun kürenin merkezindeki değerleri,
u 'nun küre üzerindeki değerlerinin ortalama değerleridir. Bu ortalama değer özelliği ise ivedilikle sabit olmayan bir fonksiyonun maksimum değerini kürenin içinde alamayacağı sonucunu verir.
Laplace denklemi Matematikte Laplace denklemi, özellikleri ilk defa
Pierre-Simon Laplace tarafından çalışılmış bir
kısmi diferansiyel denklemdir. Laplace denkleminin çözümleri, elektromanyetizma, astronomi ve akışkanlar dinamiği gibi birçok bilim alanında önemlidir çünkü çözümler bilhassa elektrik ve yerçekim
potansiyeli ile akışkan potansiyelinin davranışını açıklar. Laplace denkleminin çözümlerinin genel teorisi aynı zamanda
potansiyel teorisi olarak da bilinmektedir.
Tanım
Üç boyutta, problem
x,
y ve
z gibi üç gerçel değişkene sahip, iki kere
türevlenebilir, gerçel değerli ve
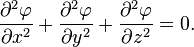
denklemini sağlayan bir

fonksiyonu bulmaktır.
Çoğunlukla bu denklem

denklemi olarak veya div'in
diverjansı ve grad'ın ise
gradyanı temsil ettiği
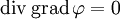
denklemi olarak veya Δ'nın
Laplace operatörü olduğu
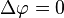
denklemi olarak yazılır.
Laplace denkleminin çözümlerine aynı zamanda
harmonik fonksiyonlar da denmektedir.
Denklemin sağ tarafı eğer belli bir
f(
x,
y,
z) fonksiyonu şeklinde verilirse, yani denklem

olarak ifade edilirse, o zaman denkleme "
Poisson denklemi" adı verilir.
Laplace ve Poisson denklemleri
eliptik kısmi diferansiyel denklemlerin en basit örnekleridir. Kısmi diferansiyel operatörü olan ve herhangi bir boyutta tanımlanabilen
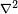
'ye veya
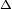
'ya
Laplace operatörü veya kısaca
Laplasyen denmektedir.
Sınır koşulları
Laplace denklemi için
Dirichlet problemi bir
D bölgesi üzerinde tanımlı ve verilmiş başka bir fonksiyona
D 'nin sınırı üzerinde eşit olan bir

fonksiyonu bulmaktan ibarettir. Laplace operatörü
ısı denkleminde yer aldığı için, problemin bir diğer yorumu da şöyledir: Bölgenin sınırındaki sıcaklık sabit tutulur ve bölgenin iç tarafındaki sıcaklık artık değişmeyecek şekilde beklenilir. İç bölgedeki sıcaklık dağılımı artık ilişkin Dirichlet probleminin çözümü tarafından verilecektir.
Laplace denklemi için
Neumann sınır koşulları D'nin sınırında

fonsiyonunu belirtmez ancak bu fonksiyonun normal türevini belirtir. Fiziksel olarak bu durum, yalnız
D'nin sınırında etkisi bilinen bir vektör alanı için olan bir potansiyelin inşasına (oluşturulmasına) denk gelmektedir.
Laplace denkleminin çözümlerine
harmonik fonksiyonlar denilmektedir ve bu fonksiyonların hepsi denklemin sağlandığı bölge içinde
analitiktir. Eğer iki fonksiyon Laplace denkleminin (veya herhangi doğrusal homojen diferansiyel denklemin) çözümüyse, toplamları (veya herhangi doğrusal kombinasyonları) da ayrıca bir çözümdür.
Süperpozisyon ilkesi de denilen bu özellik özellikle karmaşık problemlerin basit çözümlerin toplanılması yoluyla yapılan çözümlerinde çok yararlıdır.
İki boyutta Laplace denklemi
İki değişkenli Laplace denklemi
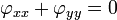
formuna sahiptir.
Analitik fonksiyonlar
Karmaşık analitik bir fonksiyonun gerçel ve sanal kısmının her ikisi de Laplace denklemini sağlar. Eğer
z=
x+
iy ise ve
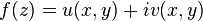
ise, o zaman
f(
z) 'nin analitik olması için gerekli koşul aşağıdaki Cauchy-Riemann denklemlerinin sağlanmasıdır:

Takip eden ifade ise
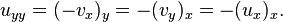
olacaktır. Bu yüzden
u Laplace denklemini sağlar. Benzer bir hesaplama yine
v 'nin de Laplace denklemini sağladığını gösterir.
Aksine diğer taraftan bir harmonik fonksiyon verilirse, bu fonksiyon analitik bir
f(
z) fonksiyonunun gerçel kısmı olur (en azından yerel olarak). Eğer

olarak alınırsa ve

şartı konulursa, o zaman Cauchy-Riemann denklemleri sağlanacaktır.
Bu ilişki ψ'yi belirlemese de artışlarını belirler:

φ için Laplace denklemi ψ'nin integrallenebilme koşulunun sağlandığını gösterir:
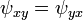
ve bu yüzden ψ bir çizgi integrali yoluyla tanımlanabilir. İntegrallenebilme koşulu ve
Stoke teoremi iki noktayı birleştiren çizgi integralinin değerinin takip edilen yoldan bağımsız olduğunu gösterir. Laplace denkleminin sonucunda çıkan çözüm çiftine
eşlenik harmonik fonksiyonlar adı verilir. Bu inşa sadece yerel olarak veya takip edilen yolun bir tekilliği çevrelememesi koşuluyla geçerlidir. Örneğin,
r ve θ kutupsal koordinatlar olursa ve

ise, o zaman karşılık gelen analitik fonksiyon

fonksiyonudur. Bununla birlikte, θ açısı orijini çevrelemeyen bir bölge içinde tek (bir) değerlidir.
Laplace denklemi ve analitik fonksiyonlar arasındaki yakın ilişki Laplace denkleminin çözümünün her mertebeden türevi olduğunu gösterir ve bu çözüm en azından bir tekilliği çevrelemeyen bir çember içinde kuvvet serilerine genişletilebilir. Bu durum, daha az düzenliliğe sahip
ısı denklemi çözümleriyle tezat bir haldedir.
Kuvvet serileri ve Fourier serileri arasında sıkı bir ilişki vardır. Bir
f fonksiyonu
R yarıçaplı bir çember içinde kuvvet serisine genişletilirse, bu gerçel ve sanal kısımları
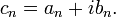
şeklinde olan uygun katsayıların olduğu

ifadesi anlamına gelir. Bu yüzden,

olur ki bu da
f 'nin Fourier seridir.
Akışkan akımı u ve
v nicelikleri durağan sıkıştırılamaz, dönmez bir akımın iki boyutta yatay ve dikey bileşenleri olsun. Akımın sıkıştırılamaz olmasının koşulu,

olmasıdır ve akımın dönmez olmasının şartı da

olmasıdır. Bir ψ fonksiyonunun diferansiyeli
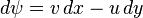
olarak tanımlanırsa, o zaman sıkıştırılamama şartı bu diferansiyel için integrallenebilme koşulu olur: Sonuçtaki fonksiyona
akış fonksiyonu adı verilir çünkü bu fonksiyon akım çizgileri boyunca sabittir. ψ'nin birinci türevi

ile verilir ve sıkıştırılamama şartı ψ 'nin Laplace denklemini sağladığını gösterir. ψ 'ye eşlenik olan harmonik φ fonksiyonuna
hız potansiyeli denilir. Cauchy-Riemann denklemleri

ifadesini verir.
Bu yüzden her analitik fonksiyon düzlemde durağan sıkıştırılamaz, dönmez bir akışkan akıma karşılık gelir. Gerçel kısım hız potansiyeli olurken sanal kısım akış fonksiyonu olur.
Elektrostatik Maxwell denklemleri'ne göre, iki uzay boyutunda yer alan ve zamandan bağımsız olan bir elektrik alanı (
u,
v),
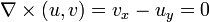
ifadesini ve ρ'nun yük yoğunluğu olduğu
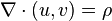
ifadesini sağlar.
Birinci Maxwell denklemi
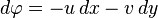
diferansiyeli için integrallenebilme koşuludur. Böylece elektrik potansiyeli olan φ

ifadesini sağlayacak şekilde inşa edilebilir.
İkinci Maxwell denklemi o zaman
Poisson denklemi olarak ifade edilen

denklemini verir.
İki boyutta kullanılana benzer olarak, Laplace denklemi elektrostatik ve akışkan akımının üç boyutlu problemlerinde de kullanılabilir.
Üç boyutta Laplace denklemi Temel çözüm
Laplace denkleminin temel çözümü, Dirac delta fonksiyonu δ'nın
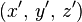
noktasında toplanmış bir birim kaynağı gösterdiği
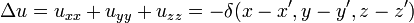
denklemini sağlar. Hiçbir fonksiyon bu özelliğe sahip değildir ancak yine de bu, integralleri uzay üzerinde birlik olan ve desteği (fonksiyonun sıfır olmadığı bölge) bir noktaya küçülen bir fonksiyonlar limiti olarak düşünülebilir. Temel çözümün tanımı bu yüzden,
u 'nun Laplasyeninin kaynak noktasını çevreleyen herhengi bir hacim üzerinde integrali alındığında, o zaman

olduğunu gösterir.
Laplace denklemi koordinatların rotasyonuyla değişmez kalır ve bu yüzden bir temel çözümün, sadece (kaynak noktasından uzaklığı gösteren)
r 'ye bağımlı olan çözümler arasından elde edilebileceği beklenir. Hacim kaynak noktası etrafında
a yarıçaplı bir top olarak düşünülürse, o zaman Gauss diverjans teoremi

ifadesini verir. O zaman takip eden ifade ise, kaynak noktası etrafında
r yarıçaplı bir küre üzerindeki

ifadesidir ve bu yüzden

olur. Benzer bir hesap ise iki boyutta

olduğunu gösterir.
Green fonksiyonu
Bir
Green fonksiyonu da bir
V hacminin
S sınırındaki uygun şartı sağlayan temel bir çözümdür. Örneğin,

,


ifadelerini sağlayabilir.
Eğer
u,
V üzerinde Poisson denkleminin herhangi bir çözümüyse

olur ve
u,
S üzerinde
g sınır değerlerini alır. O zaman aşağıdaki eşitlikleri veren (diverjans teoreminin bir sonucu olan)
Green özdeşliğine başvurulabilir:
 un
un ve
Gn gösterimleri
S üzerindeki normal türevleri ifade etmektedir.
u ve
G 'nin sağladığı şartlar bağlamında, bu sonuç
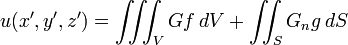
haline gelir.
Bu yüzden, Green fonksiyonu
f ve
g 'nin

noktalarındaki etkisini açıklar.
a yarıçaplı kürenin içi düşünüldüğünde ise, Green fonksiyonu yansıtma yoluyla elde edilebilir (Sommerfeld, 1949): Kürenin merkezinden ρ kadar uzaklıkta olan
P kaynak noktası,

uzaklıkta bulunan bir
N noktasına yarıçapsal doğru boyunca yansıtılır.
Unutulmaması gereken nokta
P küre içindeyse,
N 'nin küre dışında olması gerektiğidir. O zaman Green fonksiyonu
R 'nin
P kaynak noktasına uzaklığı ve
T 'nin yansıtılmış
N noktasına olan uzaklığı gösterdiği

ifadesi tarafından verilir. Green fonksiyonu için olan bu ifadenin bir sonucu ise
Poisson integral formülüdür. ρ, θ, ve φ,
P kaynak noktası için
küresel koordinatlar olsun. Burada θ dikey eksenle olan açıyı göstermektedir. (Amerikan matematik gösterimine uymaz ancak standard Avrupa ve fiziksel uygulamalarına uyum gösteren bir gösterimdir) O zaman, küre içindeki Laplace denkleminin çözümü

olarak alınırsa

tarafından verilir.
Bu formülün basit bir sonucu ise şudur:
u harmonikse, o zaman
u 'nun kürenin merkezindeki değerleri,
u 'nun küre üzerindeki değerlerinin ortalama değerleridir. Bu ortalama değer özelliği ise ivedilikle sabit olmayan bir fonksiyonun maksimum değerini kürenin içinde alamayacağı sonucunu verir.



 Denklem nedir, örnek verir misiniz?
Denklem nedir, örnek verir misiniz? ve
ve Genelde u ve v çifti, karmaşık değerli bir f(x + iy) = u(x,y) + iv(x,y) fonksiyonunun gerçel ve sanal kısımları olarak alınır. u ve v, C 'nin açık bir kümesinde sürekli şekilde türevlenebilir bir fonksiyon olsun. O zaman, f=u+iv ancak ve ancak u ve v Cauchy-Riemann denklemlerini ((1a)'yı ve (1b)'yi) sağlarsa, holomorfiktir.
Genelde u ve v çifti, karmaşık değerli bir f(x + iy) = u(x,y) + iv(x,y) fonksiyonunun gerçel ve sanal kısımları olarak alınır. u ve v, C 'nin açık bir kümesinde sürekli şekilde türevlenebilir bir fonksiyon olsun. O zaman, f=u+iv ancak ve ancak u ve v Cauchy-Riemann denklemlerini ((1a)'yı ve (1b)'yi) sağlarsa, holomorfiktir. karmaşık formunda yazılabilirler.
karmaşık formunda yazılabilirler. ve
ve  olacak şekilde,
olacak şekilde,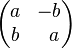 formunda olmasına karşılık gelir. Bu formdaki bir matris bir karmaşık sayının matris temsilidir. Geometrik olarak, böyle bir matris her zaman homotetisi olan bir rotasyonun bileşkesidir ve bilhassa açıları korur. Sonuç olarak, türevi sıfırdan farklı, Cauchy-Riemann denklemlerini sağlayan bir fonksiyon düzlemdeki eğriler arasındaki açıyı korur. Yani, Cauchy-Riemann denklemleri bir fonksiyonun açıkorur gönderim olması için olan koşullardır.
formunda olmasına karşılık gelir. Bu formdaki bir matris bir karmaşık sayının matris temsilidir. Geometrik olarak, böyle bir matris her zaman homotetisi olan bir rotasyonun bileşkesidir ve bilhassa açıları korur. Sonuç olarak, türevi sıfırdan farklı, Cauchy-Riemann denklemlerini sağlayan bir fonksiyon düzlemdeki eğriler arasındaki açıyı korur. Yani, Cauchy-Riemann denklemleri bir fonksiyonun açıkorur gönderim olması için olan koşullardır. Burada, türev operatörü
Burada, türev operatörü 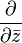
 olarak tanımlanmıştır.
olarak tanımlanmıştır. değişkeninden bağımsızdır" olarak yorumlanabilir.
değişkeninden bağımsızdır" olarak yorumlanabilir. olarak tanımlanır.
olarak tanımlanır. elde edilir. Diğer taraftan sanal eksen boyunca yaklaşılırsa
elde edilir. Diğer taraftan sanal eksen boyunca yaklaşılırsa elde edilir. İki eksen boyunca alınan türevlerin eşitliği
elde edilir. İki eksen boyunca alınan türevlerin eşitliği ifadesini verecektir. Farkedilirse bu, z0 noktasındaki (2) nolu Cauchy-Riemann denklemidir.
ifadesini verecektir. Farkedilirse bu, z0 noktasındaki (2) nolu Cauchy-Riemann denklemidir. 'nin birim dik ve pozitif yönlü olduğu herhangi (n(x,y), s(x,y)) koordinatı için de
'nin birim dik ve pozitif yönlü olduğu herhangi (n(x,y), s(x,y)) koordinatı için de eşitlikleri sağlanır. Sonuç olarak, özellikle, z=reiθ olarak verilen kutupsal koordinatlar sisteminde, denklemler
eşitlikleri sağlanır. Sonuç olarak, özellikle, z=reiθ olarak verilen kutupsal koordinatlar sisteminde, denklemler halini alır.
halini alır.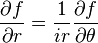 elde edilir.
elde edilir.
 Bu denklemler genellikle bir denklemde toplanırlar (f=u+iv ve φ=(α+iβ)/2):
Bu denklemler genellikle bir denklemde toplanırlar (f=u+iv ve φ=(α+iβ)/2): Eğer φ, Ck ise, o zaman herhangi sınırlı bir D bölgesinin kapanışında φ sürekli olduğu sürece, homojen olmayan denklem D 'de açık olarak çözülebilir. Aslında Cauchy integral formülü kullanılarak her ζ∈D için
Eğer φ, Ck ise, o zaman herhangi sınırlı bir D bölgesinin kapanışında φ sürekli olduğu sürece, homojen olmayan denklem D 'de açık olarak çözülebilir. Aslında Cauchy integral formülü kullanılarak her ζ∈D için ifadesi elde edilir.
ifadesi elde edilir. Cauchy-Riemann denklemlerini sağlar ancak z=0 noktasında sürekli değildir.
Cauchy-Riemann denklemlerini sağlar ancak z=0 noktasında sürekli değildir.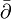 d-bar operatörü holomorfik fonksiyonları imha eder. Bu doğrudan
d-bar operatörü holomorfik fonksiyonları imha eder. Bu doğrudan alınarak şu genelleştirmeyi yapar:
alınarak şu genelleştirmeyi yapar:


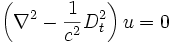
 operatörü
operatörü 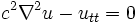
 : u'nun zamana göre 2. türevi
: u'nun zamana göre 2. türevi 
 : d'Alembert İşlemcisi Burada c dalganın yayılma veya ilerleme hızıdır. Dalganın dağılması, yani ilerledikçe başka başka frekanslar haline bürünmesi olgusu (dispersion) göz önüne alınırsa denklemde c yerine faz hızı
: d'Alembert İşlemcisi Burada c dalganın yayılma veya ilerleme hızıdır. Dalganın dağılması, yani ilerledikçe başka başka frekanslar haline bürünmesi olgusu (dispersion) göz önüne alınırsa denklemde c yerine faz hızı  kullanılır. Ayrıca daha gerçekçi sistemlerde hızın, dalganın genliğine bağlı olduğu dikkate alındığından denklem doğrusal olmayan
kullanılır. Ayrıca daha gerçekçi sistemlerde hızın, dalganın genliğine bağlı olduğu dikkate alındığından denklem doğrusal olmayan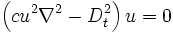

 ve
ve  tanımları yapılarak zincir kuralı yardımıyla:
tanımları yapılarak zincir kuralı yardımıyla: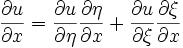 yazılabilir.
yazılabilir.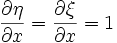 olduğundan,
olduğundan,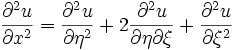 ifadesi ve aynı yol izlenerek
ifadesi ve aynı yol izlenerek ifadesi elde edilebilir. İki denklem birbirinden çıkartılarak dalga denklemi buradan,
ifadesi elde edilebilir. İki denklem birbirinden çıkartılarak dalga denklemi buradan,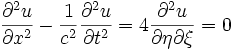 olarak yazılır. Dolayısıyla denklem,
olarak yazılır. Dolayısıyla denklem, durumuna indirgenmiş olur. Kısmî diferansiyel denklemin çözümü, tek tek değişkenler için integral alınarak
durumuna indirgenmiş olur. Kısmî diferansiyel denklemin çözümü, tek tek değişkenler için integral alınarak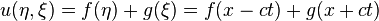 olarak bulunur. Burada f, +x yönünde ilerleyen, g de -x yönünde ilerleyen düzlem dalgayı betimler.
olarak bulunur. Burada f, +x yönünde ilerleyen, g de -x yönünde ilerleyen düzlem dalgayı betimler.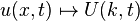 yapılırsa
yapılırsa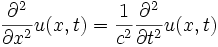 biçimine dönüşür.
biçimine dönüşür.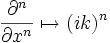 denkliği kullanılarak
denkliği kullanılarak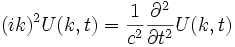 diferansiyel denklemi elde edilir. Burada,
diferansiyel denklemi elde edilir. Burada, 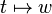 dönüşümü de uygulanarak dalga denkleminin w,k uzayındaki dağılım (dispersion) ilişkisini vermesi görülebilir. Elde edilmiş olan diferansiyel denklemin çözümü
dönüşümü de uygulanarak dalga denkleminin w,k uzayındaki dağılım (dispersion) ilişkisini vermesi görülebilir. Elde edilmiş olan diferansiyel denklemin çözümü olarak elde edilir. Ancak bu çözüm konum uzayı x de değil, başka bir uzay olan k uzayındaki çözümdür.
olarak elde edilir. Ancak bu çözüm konum uzayı x de değil, başka bir uzay olan k uzayındaki çözümdür.  Çözümün konum uzayında bulunabilmesi için k uzayındaki çözüme ters Fourier dönüşümü uygulanır.
Çözümün konum uzayında bulunabilmesi için k uzayındaki çözüme ters Fourier dönüşümü uygulanır. çözülüerek
çözülüerek Görüldüğü üzere birinci ve ikinci terim sırasıyla f ve g diye iki fonksiyonun Fourier dönüşümleri olarak kabul edilirse x uzayındaki çözüm
Görüldüğü üzere birinci ve ikinci terim sırasıyla f ve g diye iki fonksiyonun Fourier dönüşümleri olarak kabul edilirse x uzayındaki çözüm olarak elde edilir.
olarak elde edilir.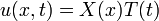 olarak yazılır ve denkleme konulursa denklem şu hali alır:
olarak yazılır ve denkleme konulursa denklem şu hali alır: iki taraf da u ya bölünürse
iki taraf da u ya bölünürse iki tane birbirinden bağımsız değişkenin olduğu ifade birbirine ancak bir sabite eşit olmaları durumunda eşit olabileceğinden iki denklem de ayrı ayrı bu sabite eşitlenerek çözümler bulunabilir. Bu sabit pozitif, negatif ve sıfır olması durumlarında incelenerek diferansiyel denklemler çözülebilir ancak fizikte zaman genelde salınım olarak ortaya çıktığından sabit, − k2, k:reel seçilerek fiziksel olarak anlamlı çözüme hızlıca gidilebilir. Böylece denklemin sol tarafından:
iki tane birbirinden bağımsız değişkenin olduğu ifade birbirine ancak bir sabite eşit olmaları durumunda eşit olabileceğinden iki denklem de ayrı ayrı bu sabite eşitlenerek çözümler bulunabilir. Bu sabit pozitif, negatif ve sıfır olması durumlarında incelenerek diferansiyel denklemler çözülebilir ancak fizikte zaman genelde salınım olarak ortaya çıktığından sabit, − k2, k:reel seçilerek fiziksel olarak anlamlı çözüme hızlıca gidilebilir. Böylece denklemin sol tarafından: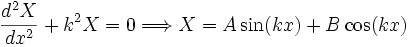 ve sağ tarafından da
ve sağ tarafından da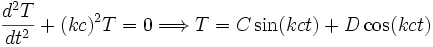 bulunur. Sinüs ve kosinüs ile elde edilen çözümler sınır koşullarını rahatça sağlayacaklarından genellikle sınır değer problemlerinde kullanılırlar. Dalga boşlukta hareket eden bir elektromanyetik bir ışınsa o zaman çözümleri K1eikx ve K2eikct olarak vermek daha rahat olur. Matematiksel olarak iki çözüm de doğru olmasına rağmen fiziksel kaidelerden serbest ve bağlı olarak çözümler böyle sınıflandırılabilir.
bulunur. Sinüs ve kosinüs ile elde edilen çözümler sınır koşullarını rahatça sağlayacaklarından genellikle sınır değer problemlerinde kullanılırlar. Dalga boşlukta hareket eden bir elektromanyetik bir ışınsa o zaman çözümleri K1eikx ve K2eikct olarak vermek daha rahat olur. Matematiksel olarak iki çözüm de doğru olmasına rağmen fiziksel kaidelerden serbest ve bağlı olarak çözümler böyle sınıflandırılabilir. şeklinde ifade edilebilir. Burada;
şeklinde ifade edilebilir. Burada; Buradaki Ψ + ve Ψ − , Dirac dönücüleri olarak adlandırılır ve her birinin farklı bir fiziksel anlamı vardır. Ψ + dönücüsü, pozitif enerjileri, Ψ − negatif enerjileri ifāde eder. Bunlar da
Buradaki Ψ + ve Ψ − , Dirac dönücüleri olarak adlandırılır ve her birinin farklı bir fiziksel anlamı vardır. Ψ + dönücüsü, pozitif enerjileri, Ψ − negatif enerjileri ifāde eder. Bunlar da ve
ve  olarak tanımlanır. ψ yukarı dönü ve φ aşağı dönü olarak anlam kazanır. Yani, dalga fonksiyonu;
olarak tanımlanır. ψ yukarı dönü ve φ aşağı dönü olarak anlam kazanır. Yani, dalga fonksiyonu; şeklindedir.
şeklindedir. biçiminde yazılabilir. Dirac matrisleri; I, birim matris olmak üzere
biçiminde yazılabilir. Dirac matrisleri; I, birim matris olmak üzere ve
ve 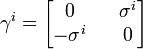 olarak Pauli matrisleri cinsinden yazılabilir. Bunlar yerine konunca Dirac denklemi,
olarak Pauli matrisleri cinsinden yazılabilir. Bunlar yerine konunca Dirac denklemi, biçimini alır. Matris çarpımı yapılırsa, çiftlenimli denklemler elde edilir:
biçimini alır. Matris çarpımı yapılırsa, çiftlenimli denklemler elde edilir: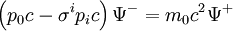
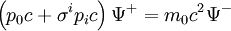 Bu özdeğer denklemlerini çözmek için, dönücülerden biri çekilip diğer denklemde yerine yazılabilir. Buradan, göreliliğin en önemli denklemlerinden biri elde edilir:
Bu özdeğer denklemlerini çözmek için, dönücülerden biri çekilip diğer denklemde yerine yazılabilir. Buradan, göreliliğin en önemli denklemlerinden biri elde edilir: Burada p0c = E = mc2 ve
Burada p0c = E = mc2 ve  olduğundan ifade,
olduğundan ifade, şeklindedir. Buradan E için pozitif ve negatif değerler gelir.
şeklindedir. Buradan E için pozitif ve negatif değerler gelir.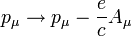 denklem,
denklem,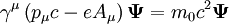 biçimine gelir. Buradaki Aμ, elektromanyetik dörtpotansiyeldir ve e elektriksel yüktür.
biçimine gelir. Buradaki Aμ, elektromanyetik dörtpotansiyeldir ve e elektriksel yüktür. Burada, m sabiti doğrunun eğimini belirler; b sabiti ise denklemin x ve y eksenlerini keseceği noktaları belirler (yani m sabiti değişmesi fonksiyonun artış miktarını etkilerken b sabitinin değişmesi doğrunun düzlemde ötelenmesine neden olur). Aynı terimde iki değişken barındıran ya da değişken terimin derecesi 1'den farklı olan denklemler: x2 ya da y1 / 3 (terimler birinci dereceden ya da bir sabit olmadığından) ve xy (tek bir terim çift değişken içerdiğinden) doğrusal değildir.
Burada, m sabiti doğrunun eğimini belirler; b sabiti ise denklemin x ve y eksenlerini keseceği noktaları belirler (yani m sabiti değişmesi fonksiyonun artış miktarını etkilerken b sabitinin değişmesi doğrunun düzlemde ötelenmesine neden olur). Aynı terimde iki değişken barındıran ya da değişken terimin derecesi 1'den farklı olan denklemler: x2 ya da y1 / 3 (terimler birinci dereceden ya da bir sabit olmadığından) ve xy (tek bir terim çift değişken içerdiğinden) doğrusal değildir.



 Hem A hem B'nin sıfıra eşit olmadığı durumalrda denklem genelde A ≥ 0 olacak şekilde yazılır. Denklemin grafiği bir doğru belirtir. A sıfır olmadıkça denklem x eksenini değeri -C/A olan bir a noktasında keser, B sıfır olmadıkça denklem y eksenini değeri -C/B olan bir b noktasında keser. A/B ise denklemin eğimini (m'yi) verir.
Hem A hem B'nin sıfıra eşit olmadığı durumalrda denklem genelde A ≥ 0 olacak şekilde yazılır. Denklemin grafiği bir doğru belirtir. A sıfır olmadıkça denklem x eksenini değeri -C/A olan bir a noktasında keser, B sıfır olmadıkça denklem y eksenini değeri -C/B olan bir b noktasında keser. A/B ise denklemin eğimini (m'yi) verir.  A ve B sıfır olmadıkça A, B, ve C en büyük ortak çarpanı 1 olan tamsayılardan seçilir. Genelde A ≥ 0'dir. A sıfır olmadıkça denklem x eksenini değeri C/A olan bir a noktasında keser, B sıfır olmadıkça denklem y eksenini değeri C/B olan bir b noktasında keser. A/B ise denklemin eğimini (m'yi) verir.
A ve B sıfır olmadıkça A, B, ve C en büyük ortak çarpanı 1 olan tamsayılardan seçilir. Genelde A ≥ 0'dir. A sıfır olmadıkça denklem x eksenini değeri C/A olan bir a noktasında keser, B sıfır olmadıkça denklem y eksenini değeri C/B olan bir b noktasında keser. A/B ise denklemin eğimini (m'yi) verir.  m eğimi ve b de y-ekseni kesim noktasını gösterir. x = 0 de y = b olduğu direk gözlenir.
m eğimi ve b de y-ekseni kesim noktasını gösterir. x = 0 de y = b olduğu direk gözlenir.  m eğim ve (x1,y1) doğru üzerinde herhangi bir noktadır. Bazen nokta-eğim formü şu şekilde de karşımıza çıkabilir:
m eğim ve (x1,y1) doğru üzerinde herhangi bir noktadır. Bazen nokta-eğim formü şu şekilde de karşımıza çıkabilir:  Ancak, bu şekilde x = x1 durumunda eşitlik sağlanmaz.
Ancak, bu şekilde x = x1 durumunda eşitlik sağlanmaz.  E ve F sıfırdan farklı olmalıdır. Doğru ve x ekseninin kesiştiği nokta (x ekseninin kesim noktası) E ve y ekseninin kesim noktası F'dir. A = 1/E, B = 1/F ve C = 1 alınarak kolaylıkla standart forma dönüştürülebilir.
E ve F sıfırdan farklı olmalıdır. Doğru ve x ekseninin kesiştiği nokta (x ekseninin kesim noktası) E ve y ekseninin kesim noktası F'dir. A = 1/E, B = 1/F ve C = 1 alınarak kolaylıkla standart forma dönüştürülebilir.  p ≠ h. Grafik (h,k)'ya karşılık (p,q) noktasını sağlar ve eğim m = (q−k) / (p−h)'dir.
p ≠ h. Grafik (h,k)'ya karşılık (p,q) noktasını sağlar ve eğim m = (q−k) / (p−h)'dir. 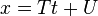 ve
ve  olsun şeklinde iki denklemdir. eğim m = V / T, x-kesim noktası a=(VU−WT) / V ve y-kesim noktası b=(WT−VU) / T
olsun şeklinde iki denklemdir. eğim m = V / T, x-kesim noktası a=(VU−WT) / V ve y-kesim noktası b=(WT−VU) / T  φ normalin eğim açısı ve p de normalin uzunluğudur. Normal doğru ve başlangıç noktası (orijin) arasında doğruya dik olacak en kısa doğru parçasıdır. Tüm katsayılar by
φ normalin eğim açısı ve p de normalin uzunluğudur. Normal doğru ve başlangıç noktası (orijin) arasında doğruya dik olacak en kısa doğru parçasıdır. Tüm katsayılar by  'a bölünerek ve eğer C > 0'sa tüm katsayılar -1'le çarpılarak (böylece son katsayı negatif olur) rahatça bulunabilir. Alman Matematikçi Ludwig Otto Hesse'nin anısına bu form ayrıca Hesse standart formu olarak da anılır. Bazen denklemlerde sadeleştirme işlemlerinden sonra eşitsizlik söz konusu olabilir, 1 = 0 gibi. Bu gibi eşitsizlikler tutarsız eşitsizliklerdir, yani hiç bir x ve y değeri için doğru değildir. 3x + 2 = 3x − 5 buna örnek olabilir.
'a bölünerek ve eğer C > 0'sa tüm katsayılar -1'le çarpılarak (böylece son katsayı negatif olur) rahatça bulunabilir. Alman Matematikçi Ludwig Otto Hesse'nin anısına bu form ayrıca Hesse standart formu olarak da anılır. Bazen denklemlerde sadeleştirme işlemlerinden sonra eşitsizlik söz konusu olabilir, 1 = 0 gibi. Bu gibi eşitsizlikler tutarsız eşitsizliklerdir, yani hiç bir x ve y değeri için doğru değildir. 3x + 2 = 3x − 5 buna örnek olabilir. ve
ve a bir sayıdır. Bunları sağlayan fonksiyonlara doğrusal fonksiyon denir.
a bir sayıdır. Bunları sağlayan fonksiyonlara doğrusal fonksiyon denir. Burada, a1, a2, …, an katsayılar, x1, x2, …, xn değişkenlerdir, ve b de sabittir. Üç değişkenli denklemlerde genelde x1 yerine sadece x, x2 sadece y ve x3 yerine z kullanılır.
Burada, a1, a2, …, an katsayılar, x1, x2, …, xn değişkenlerdir, ve b de sabittir. Üç değişkenli denklemlerde genelde x1 yerine sadece x, x2 sadece y ve x3 yerine z kullanılır.
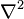 (Δ biciminde de gosterilir)
(Δ biciminde de gosterilir) 
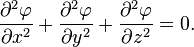 denklemini sağlayan bir
denklemini sağlayan bir  fonksiyonu bulmaktır.
fonksiyonu bulmaktır. denklemi olarak veya div'in
denklemi olarak veya div'in 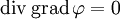 denklemi olarak veya Δ'nın
denklemi olarak veya Δ'nın 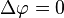 denklemi olarak yazılır.
denklemi olarak yazılır. olarak ifade edilirse, o zaman denkleme "
olarak ifade edilirse, o zaman denkleme "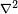 'ye veya
'ye veya 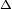 'ya
'ya  fonksiyonu bulmaktan ibarettir. Laplace operatörü
fonksiyonu bulmaktan ibarettir. Laplace operatörü 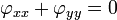 formuna sahiptir.
formuna sahiptir.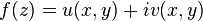 ise, o zaman f(z) 'nin analitik olması için gerekli koşul aşağıdaki Cauchy-Riemann denklemlerinin sağlanmasıdır:
ise, o zaman f(z) 'nin analitik olması için gerekli koşul aşağıdaki Cauchy-Riemann denklemlerinin sağlanmasıdır: Takip eden ifade ise
Takip eden ifade ise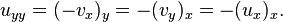 olacaktır. Bu yüzden u Laplace denklemini sağlar. Benzer bir hesaplama yine v 'nin de Laplace denklemini sağladığını gösterir.
olacaktır. Bu yüzden u Laplace denklemini sağlar. Benzer bir hesaplama yine v 'nin de Laplace denklemini sağladığını gösterir. olarak alınırsa ve
olarak alınırsa ve şartı konulursa, o zaman Cauchy-Riemann denklemleri sağlanacaktır.
şartı konulursa, o zaman Cauchy-Riemann denklemleri sağlanacaktır. φ için Laplace denklemi ψ'nin integrallenebilme koşulunun sağlandığını gösterir:
φ için Laplace denklemi ψ'nin integrallenebilme koşulunun sağlandığını gösterir: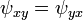 ve bu yüzden ψ bir çizgi integrali yoluyla tanımlanabilir. İntegrallenebilme koşulu ve
ve bu yüzden ψ bir çizgi integrali yoluyla tanımlanabilir. İntegrallenebilme koşulu ve  ise, o zaman karşılık gelen analitik fonksiyon
ise, o zaman karşılık gelen analitik fonksiyon fonksiyonudur. Bununla birlikte, θ açısı orijini çevrelemeyen bir bölge içinde tek (bir) değerlidir.
fonksiyonudur. Bununla birlikte, θ açısı orijini çevrelemeyen bir bölge içinde tek (bir) değerlidir.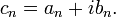 şeklinde olan uygun katsayıların olduğu
şeklinde olan uygun katsayıların olduğu ifadesi anlamına gelir. Bu yüzden,
ifadesi anlamına gelir. Bu yüzden, olur ki bu da f 'nin Fourier seridir.
olur ki bu da f 'nin Fourier seridir. olmasıdır ve akımın dönmez olmasının şartı da
olmasıdır ve akımın dönmez olmasının şartı da olmasıdır. Bir ψ fonksiyonunun diferansiyeli
olmasıdır. Bir ψ fonksiyonunun diferansiyeli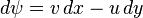 olarak tanımlanırsa, o zaman sıkıştırılamama şartı bu diferansiyel için integrallenebilme koşulu olur: Sonuçtaki fonksiyona
olarak tanımlanırsa, o zaman sıkıştırılamama şartı bu diferansiyel için integrallenebilme koşulu olur: Sonuçtaki fonksiyona  ile verilir ve sıkıştırılamama şartı ψ 'nin Laplace denklemini sağladığını gösterir. ψ 'ye eşlenik olan harmonik φ fonksiyonuna
ile verilir ve sıkıştırılamama şartı ψ 'nin Laplace denklemini sağladığını gösterir. ψ 'ye eşlenik olan harmonik φ fonksiyonuna  ifadesini verir.
ifadesini verir.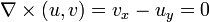 ifadesini ve ρ'nun yük yoğunluğu olduğu
ifadesini ve ρ'nun yük yoğunluğu olduğu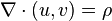 ifadesini sağlar.
ifadesini sağlar.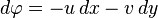 diferansiyeli için integrallenebilme koşuludur. Böylece elektrik potansiyeli olan φ
diferansiyeli için integrallenebilme koşuludur. Böylece elektrik potansiyeli olan φ denklemini verir.
denklemini verir.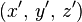 noktasında toplanmış bir birim kaynağı gösterdiği
noktasında toplanmış bir birim kaynağı gösterdiği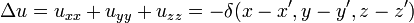 denklemini sağlar. Hiçbir fonksiyon bu özelliğe sahip değildir ancak yine de bu, integralleri uzay üzerinde birlik olan ve desteği (fonksiyonun sıfır olmadığı bölge) bir noktaya küçülen bir fonksiyonlar limiti olarak düşünülebilir. Temel çözümün tanımı bu yüzden, u 'nun Laplasyeninin kaynak noktasını çevreleyen herhengi bir hacim üzerinde integrali alındığında, o zaman
denklemini sağlar. Hiçbir fonksiyon bu özelliğe sahip değildir ancak yine de bu, integralleri uzay üzerinde birlik olan ve desteği (fonksiyonun sıfır olmadığı bölge) bir noktaya küçülen bir fonksiyonlar limiti olarak düşünülebilir. Temel çözümün tanımı bu yüzden, u 'nun Laplasyeninin kaynak noktasını çevreleyen herhengi bir hacim üzerinde integrali alındığında, o zaman olduğunu gösterir.
olduğunu gösterir. ifadesini verir. O zaman takip eden ifade ise, kaynak noktası etrafında r yarıçaplı bir küre üzerindeki
ifadesini verir. O zaman takip eden ifade ise, kaynak noktası etrafında r yarıçaplı bir küre üzerindeki ifadesidir ve bu yüzden
ifadesidir ve bu yüzden olur. Benzer bir hesap ise iki boyutta
olur. Benzer bir hesap ise iki boyutta olduğunu gösterir.
olduğunu gösterir. ,
,
 ifadelerini sağlayabilir.
ifadelerini sağlayabilir. olur ve u, S üzerinde g sınır değerlerini alır. O zaman aşağıdaki eşitlikleri veren (diverjans teoreminin bir sonucu olan)
olur ve u, S üzerinde g sınır değerlerini alır. O zaman aşağıdaki eşitlikleri veren (diverjans teoreminin bir sonucu olan)  un ve Gn gösterimleri S üzerindeki normal türevleri ifade etmektedir. u ve G 'nin sağladığı şartlar bağlamında, bu sonuç
un ve Gn gösterimleri S üzerindeki normal türevleri ifade etmektedir. u ve G 'nin sağladığı şartlar bağlamında, bu sonuç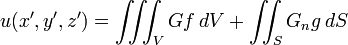 haline gelir.
haline gelir. noktalarındaki etkisini açıklar. a yarıçaplı kürenin içi düşünüldüğünde ise, Green fonksiyonu yansıtma yoluyla elde edilebilir (Sommerfeld, 1949): Kürenin merkezinden ρ kadar uzaklıkta olan P kaynak noktası,
noktalarındaki etkisini açıklar. a yarıçaplı kürenin içi düşünüldüğünde ise, Green fonksiyonu yansıtma yoluyla elde edilebilir (Sommerfeld, 1949): Kürenin merkezinden ρ kadar uzaklıkta olan P kaynak noktası, uzaklıkta bulunan bir N noktasına yarıçapsal doğru boyunca yansıtılır.
uzaklıkta bulunan bir N noktasına yarıçapsal doğru boyunca yansıtılır. ifadesi tarafından verilir. Green fonksiyonu için olan bu ifadenin bir sonucu ise
ifadesi tarafından verilir. Green fonksiyonu için olan bu ifadenin bir sonucu ise  olarak alınırsa
olarak alınırsa tarafından verilir.
tarafından verilir.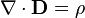
 Manyetizma için Gauss Yasası
Manyetizma için Gauss Yasası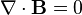
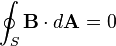
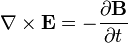
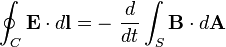

 Bu tablodaki semboller ve onlara karşılık gelen
Bu tablodaki semboller ve onlara karşılık gelen 
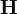
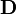

 serbest
serbest 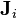 iletkenlik
iletkenlik 
 S yüzeyini kapatan diferansiyel V hacmi metreküp
S yüzeyini kapatan diferansiyel V hacmi metreküp 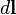 S yüzeyini çevreleyen C
S yüzeyini çevreleyen C 
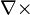
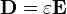

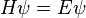 Burada H, Hamiltonyen' i temsil eder. Hamiltonyen, parçacığın toplam enerjisini veren bir operatördür ve
Burada H, Hamiltonyen' i temsil eder. Hamiltonyen, parçacığın toplam enerjisini veren bir operatördür ve 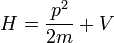 şeklinde ifade edilir. İlk terim kinetik enerjiyi, ikinci terim ise potansiyel enerjiyi temsil eder. Momentum operatörü
şeklinde ifade edilir. İlk terim kinetik enerjiyi, ikinci terim ise potansiyel enerjiyi temsil eder. Momentum operatörü  denklemde yerine konursa Schrödinger denkleminin sol tarafı elde edilir.
denklemde yerine konursa Schrödinger denkleminin sol tarafı elde edilir. Bu zamana bağlı Schrödinger denklemidir. Denklemin sağ tarafının sıfıra eşit olması durumunda zamandan bağımsız Schrödinger denklemi karşımıza çıkar. Burada
Bu zamana bağlı Schrödinger denklemidir. Denklemin sağ tarafının sıfıra eşit olması durumunda zamandan bağımsız Schrödinger denklemi karşımıza çıkar. Burada  değerinde Planck sabiti, m; parçacığın kütlesi, V; potansiyel enerji,
değerinde Planck sabiti, m; parçacığın kütlesi, V; potansiyel enerji, 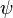 ; parçacığa eşlik eden
; parçacığa eşlik eden  şeklinde olur. Bu sayede elde edilen Schrödinger denklemine, Relativistik (göreli) Schrödinger Denklemi denir ve
şeklinde olur. Bu sayede elde edilen Schrödinger denklemine, Relativistik (göreli) Schrödinger Denklemi denir ve  olmak üzere şu formda yazılır.
olmak üzere şu formda yazılır. Denklemin çözümü için, parçacığın bulunduğu duruma göre içinde olduğu potansiyeller şöyle özetlenebilir:
Denklemin çözümü için, parçacığın bulunduğu duruma göre içinde olduğu potansiyeller şöyle özetlenebilir:



