Legendre Dönüşümü
Vikipedi, özgür ansiklopedi

Legendre dönüşümü, bir fonksiyonu başka değişkenlerle ifade etmenin bir yoludur. Örnek olarak bir f(x) fonksiyonunun Legendre dönüşümü incelenebilir.
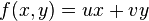
fonksiyonunun tam diferansiyeli alınırsa,

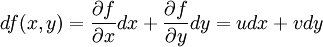
Dönüşüm için bir g fonksiyonu tanımlansın bu,

şeklinde verilsin. g fonksiyonunun tam diferansiyeli,

biçiminde verilir. Dolayısıyla g fonksiyonu f fonksiyonundan farklı olarak x ve y değişkenleriyle değil, u ve y değişkenleriyle ifade edilmiş olur. Bu g fonksiyonu tanımı f' in bir Legendre dönüşümüdür. Bunun dışında iki eşitlik arasında bir ilişki de gözlenebilir. x ve y değişkenlerinin çarpanları u ve v için ilk denlemden,
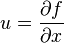
ve
ifadeleri yazılabilir. Legendre dönüştürülmüş fonksiyon için aynı şekilde ifadeler yazılırsa,
ve
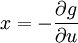
ifadeleri elde edilir. Legendre dönüşümleri özellikle istatistik mekanikte kullanılır. Helmholtz ve Gibbs serbest enerjileri birer Legendre dönüşümüdür. Bunun dışında Lagrange mekaniğinden Hamilton mekaniğine geçiş yapılırken yazılan Hamilton denklemleri de aslen birer Legendre dönüşümüdür.


Alıntıdır