Bileşke kuvvet, bir cisme uygulanan kuvvetlerin birleşimidir. Eğer f, X kümesinden Y kümesine giden bir fonksiyonsa, g de Y kümesinden Z kümesine giden bir fonksiyonsa, o zaman fonksiyonunu, her için,

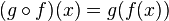
kuralıyla tanımlanan X kümesinden Z kümesine giden fonksiyon olarak tanımlanır. Bu fonksiyona g ve f fonksiyonlarının bileşkesi adı verilir. (İngilizcesi "composition").
Demek ki bileşke,
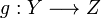
ve fonksiyonlarından,

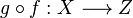
fonksiyonunu üretir.
Dikkat: yazılımında f ve g'nin sıralamalarına dikkat edin!
İkinci Dikkat: g ve f fonksiyonlarının (bu sırayla) bileşkesini alabilmek için f fonksiyonunun varış kümesi, g fonksiyonunun kalkış kümesine eşit olmalıdır.
Eğer f, X kümesinden Y kümesine, g de Y kümesinden X kümesine giden bir fonksiyonsa, o zaman hem fonksiyonundan, hem de fonksiyonundan söz edebiliriz.
Bileşke, X'ten X'e giden fonksiyonlar kümesi olan Fonk kümesi üzerine bir ikili işlemdir. Özdeşlik fonksiyonu IdX, bu ikili işlemin sağdan ve soldan etkisiz elemanıdır. Ayrıca Fonk kümesinin bileşke işlemi için tersinir elemanları eşlemeler, yani bijeksiyonlardır.
Örnek: X = Y = Z = R (gerçel sayılar kümesi) olsun. f fonksiyonu f(x) = x2 ve g fonksiyonu g(x) = x + 1 olarak tanımlansın. O zaman,

dir. Ama

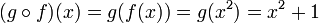
dir. Demek ki
, yani bileşkenin değişme özelliği yoktur. Öte yandan bileşkenin - şimdi açıklayacağımız -- birleşme özelliği vardır:
dört küme olsun. , ,
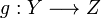
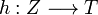
üç fonksiyon olsun. O zaman şu fonksiyonlardan söz edebiliriz:
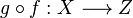
, , , . Bu fonksiyonlardan ikincisi ve dördüncüsü birbirine eşittir, yani

eşitliği geçerlidir. Bunu kanıtlayalım. X kümesinden herhangi bir x elemanı alalım ve her iki fonksiyonu da bu x elemanında değerlendirelim.

ve

Her iki eşitliğin sağ tarafları eşit olduğundan, sol tarafları da eşittir, yani
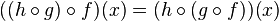
. Bundan da fonksiyonların eşit olduğu, yani eşitliği çıkar.
BİLEŞKE FONKSİYON
1. Tanım
f : A ® B
g : B ® C
olmak üzere, gof : A ® C fonksiyonuna f ile g nin bileşke fonksiyonu denir ve g bileşke f diye okunur.
(gof)(x) = g[f(x)] tir.


2. Bileşke Fonksiyonun Özellikleri
i) Bileşke işleminin değişme özelliği yoktur.
fog ¹ gof
Bazı fonksiyonlar için fog= gof olabilir. Fakat bu bileşke işleminin değişme özelliği olmadığını değiştirmez.
ii) Bileşke işleminin birleşme özelliği vardır.
fo(goh) = (fog)oh = fogoh
iii) foI = Iof = f
olduğundan I(x) = x fonksiyonu bileşke işleminin birim (etkisiz) elemanıdır.
iv) fof – 1 = f – 1of = I
olduğundan f nin bileşke işlemine göre tersi f – 1 dir.
v) (fog) – 1 = g – 1of – 1 dir.