Çember

Düzlemde sabit bir noktadan eşit uzaklıktaki noktalar kümesi.

Sabit noktaya "merkez", eşit uzaklığı ifade eden ve negatif olmayan gerçek sayıya "yarıçap" denir. Çember, düzgün kapalı bir eğridir. Çemberin farklı iki noktasını birleştiren doğru parçası "kiriş", merkezden geçen kiriş ise "çap" adını alır. Çemberin düzleminde bulunup da çemberle arakesiti yalnızca bir noktadan oluşan doğruya "teğet", ortak noktaya "teğetin değme noktası" denir. Bir çemberin herhangi bir teğetinin değme noktasıyla merkezinin belirttiği doğru, teğete diktir. Düzlemde bir doğruya aynı noktada teğet çemberlere, doğrunun aynı ya da ayrı tarafında bulunmalarına göre, içten ya da dıştan teğet çemberler denir. Köşesi bir çemberin merkezinde olan açı, "merkez açı" adını alır. Çemberin bir küçük yayının ölçüsü, bu yayı gören merkez açının ölçüsüne eşittir. Çemberin analitik incelenmesinde merkezinin koordinatlarıyla (a,b) yarıçapını (r) bilmek yeterlidir. Bu durumda çemberin denklemi (x-a)2+(y-b)2=r2 biçimindedir. Genel olarak, A2+B2-4C> O oldukça x2+y2 + Ax+By+C = O denklemi bir çemberi gösterir. Çemberin merkezi, koordinat sisteminin başlangıcıyla çakışsa (merkezil çember), denklem x2+y2=r2 biçimini alır. Bu durumda, çembere, üzerindeki bir (xo,yo) noktasından çizilen teğetin denklemi xxo+yyo=r2'dir. Teğete değme noktasında dik doğrunun (normalin) denklemiyse xyo-yxo=O biçimindedir. Örneğin x2+y2=1 birim çemberinde (1,1) noktasındaki teğetin denklemi x+y=1, normalin denklemiyse x-y=O'dur.

Bir çember

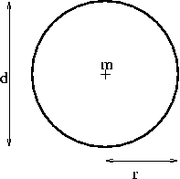
• m = merkez
• d = çap
• r = yarıçap

Düzlemde sabit bir noktaya eşit uzaklıkta bulunan noktaların kümesine çember denir ve düzlemde sabit bir noktadan eşit uzaklıkta bulunan noktaların geometrik yerini bir çember belirtir. Bu sabit noktaya çemberin merkezi, eşit uzaklıkların her birine de yarıçap denir.

Düzlemde sabit bir "O" noktasından, sabit bir "r" uzaklığında bulunan noktaların tümünün kümesine çember denir.

• "O" noktasına merkez,
• "O" noktasını çemberin herhangi bir noktasına birleştiren doğru parçasına yarıçap,
• Çemberin herhangi iki noktasını birlerştiren doğru parçasına kiriş,
• Merkezden geçen kirişe çap,
• Çemberi farklı iki noktadan kesen doğruya kesen,
• Bir noktada kesen doğruya teğet denir.

Analitik geometride çemberin denklemi x-y koordinat sisteminde şu biçimde yazılabilir:

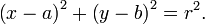
Eğer çemberin merkezi koordinat sistemi içinde (0,0) noktası olursa, yukarıdaki ifade;

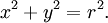
şeklinde de yazılabilir ve bu çembere birim çember denir.
Çemberin çevresi formülü:

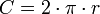
Daire

Daire, çemberin içinde kalan alana verilen addır. Burada alandan kasıt, bir çemberin çevrelediği noktaların kümesi olmasıdır. Bir dairenin açık daire ya da kapalı daire olmasını dairenin sınırlarını oluşturan çemberin daireye dahil olup olmadığı belirler; çember daireye dahilse kapalı daire, değilse açık dairedir.
Daireler genelde D harfiyle gösterilirler. Bir çemberi tanımlayan merkezi ve yarıçapı olduğu için, dairenin gösteriminde daireyi tanımlayan çemberin merkezi ve yarıçapı kullanılır. Bu nedenle, dairenin merkezi ve dairenin yarıçapı terimleri doğal olarak kullanılmaktadır. Mesela 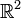'deki birim çemberin tanımladığı daireye birim daire adı verilir ve D(0,1) ile gösterilir. Burada 0 'dan kasıt 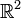'deki orijindir.

Yarıçapı r olan bir dairenin alanı 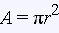formülüyle bulunur.
Çevre uzunluğu ise C = 2πr formülüyle bulunur.

Kartezyen koordinatlarda merkezi (a, b) ve yarıçapı R olan açık bir D dairesinin tanımı şu şekilde yapılmaktadır:

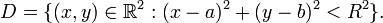
Benzer bir şekilde, aynı merkez ve yarıçapa sahip kapalı bir dairenin tanımı ise şu şekilde yapılmaktadır: