Orta Çağ matematikçileri ve buluşları hakkında bilgi verir misiniz?
Ziyaretçi
Orta Çağ matematikçileri, matematik alanında çalışmaları bulunan İslam bilginleri kimlerdir, buluşları nelerdir?
Orta Çağ matematikçileri ve buluşları hakkında bilgi verir misiniz?
Orta Çağ matematikçileri ve buluşları hakkında bilgi verir misiniz?
Ebu'l-Vefâ el-Bûzcânî
Ebu'l Vefa el-Buzcani (d. 10 Haziran 940 - ö. 1 Temmuz 998), İranlı matematikçi ve astronom.
Matematik
Ebu'l Vefa, matematik sahasında özellike trigonometri üzerinde çalışmalar yapmıştır. Trigonometrinin altı esas oranı arasındaki trigonometrik ilişkileri ilk defa ortaya koymuştur. Bu oranlar günümüzde aynen kullanılmaktadır.
Ebu'l Vefa'nın matematik tarihinde ortaya koyduğu ilk trigonometrik özdeşliklerden bazıları şunlardır:
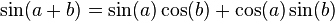
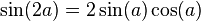
Ayrıca küresel trigonometride sinüs teoremini açıklamıştır:
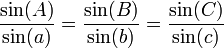
Ebu'l Vefa, Habeş el Hasib ve El Mervezi gibi önemli matematikçileri izleyerek tanjant ve sekant fonksiyonlarını tanımladı. Sekant kaşifi olarak genellikle Kopernik bilinirse de ünlü bilim tarihçilerinden Monte Candon ve Carra de Vaux'un araştırmaları sonucu bu buluşun Ebu'l Vefa'ya ait olduğu tespit edilmiştir.
Trigonometrinin yanında cebir ilmi üzerinde derinlemesine çalışmalarda bulunan Ebu'l Vefa o zamana dek bilinmeyen dördüncü dereceden denklemlerin çözümünü gerçekleştirdi.
Örneğin:
denklemini çözerken 
ve 
koniklerinin kesişmesinden istifade etti. Eski Yunanların ve Hintlerin çözemediği birçok problemi geometrik yollarla çözmeyi başardı.
Hârizmî
Hârizmî ya da tam adıyla Ebû Ca'fer Muhammed bin Mûsâ el-Hârizmî, matematik, gökbilim ve coğrafya alanlarında çalışmış Fars bilim adamı. Kökeni konusunda farklı düşünceler vardır. 780 yılında Harezm bölgesinin Hive şehrinde dünyaya gelmiştir. 850 yılında Bağdat'ta vefat etmiştir.
Cebir Alanındaki Çalışmaları
Cebir sözcüğü de Harezmi'nin "El’Kitab’ül-Muhtasar fi Hısab’il Cebri ve’l-Mukabele” (Cebir ve Denklem Hesabı Üzerine Özet Kitap) adlı eserinden gelmektedir. Bu eser aynı zamanda doğu ve batının ilk müstakil cebir kitabı olma özelliğini taşımaktadır.
Matematik alanındaki çalışmaları cebirin temelini oluşturmuştur. Bir dönem bulunduğu Hindistan’da sayıları ifade etmek için harfler ya da heceler yerine basamaklı sayı sisteminin kullanıldığını saptamıştır. Harezmî'nin bu konuda yazdığı kitabın Algoritmi de numero Indorum adıyla Latince'ye tercüme edilmesi sonucu, sembollerden oluşan bu sistem ve sıfır, 12. yüzyılda batı dünyasına sunulmuştur. Hesab-ül Cebir vel-Mukabele adlı kitabı, matematik tarihinde, birinci ve ikinci dereceden denklemlerin sistematik çözümlerinin yer aldığı ilk eserdir. Bu nedenle Harezmî (Diophantus ile birlikte) "cebirin babası" olarak da bilinir. İngilizce'deki "algebra" ve bunun Türkçe'deki karşılığı olan "cebir" sözcüğü, Harezmî'nin kitabındaki ikinci dereceden denklemleri çözme yöntemlerinden biri olan "el-cebr"den gelmektedir.
Harezmi sıfır rakamını ve x bilinmeyenini kullandığı bilinen ilk kişidir.
Battanî
Ebu Abdullah Muhammed bin Cabir bin Sinan er-Rekki es-Sabi el-Battani (858, Harran - 929, Samarra yakınlarındaki Kasr el-Cis kazası) Latince Albategnius, Albategni ya da Albatenius olarak bilinen, Arap astronom, astrolog ve matematikçidir. Şu anda Türkiye'de bulunan Urfa ilinin bir ilçesi olan Harran'da doğmuştur. Lakabı olan es-Sabi'dir fakat onun tam künyesi, bizi onun Müslüman olduğu sonucuna götürür.
Matematik
Battani, matematikte trigonometride günümüzde kullanılan formüller üretmiştir:
Ayrıca sin x = a cos x eşitliğini buldu, formül:
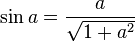
Battani,el-Mervezi'nin tanjant fikrini,tanjant ve kotanjant hesaplamaları amacıyla denklemler geliştirmek için konu hakkındaki matematiksel tablolarını derleyerek kullanmıştır.Bundan başka sekant ve kosekantın işteş fonksiyonalrını keşfetmiş ve O'nun gölgelerin tablosu olarak adlandırdığı,kosekantlar hakkındaki ilk mateamtiksel tabloyu,1'den 90'a kadar her bir dereceyi içerecek şekilde hazırlamıştır.
Vikipedi, özgür ansiklopedi
Ebu'l Vefa el-Buzcani (d. 10 Haziran 940 - ö. 1 Temmuz 998), İranlı matematikçi ve astronom.
Sponsorlu Bağlantılar
Matematik
Ebu'l Vefa, matematik sahasında özellike trigonometri üzerinde çalışmalar yapmıştır. Trigonometrinin altı esas oranı arasındaki trigonometrik ilişkileri ilk defa ortaya koymuştur. Bu oranlar günümüzde aynen kullanılmaktadır.
Ebu'l Vefa'nın matematik tarihinde ortaya koyduğu ilk trigonometrik özdeşliklerden bazıları şunlardır:
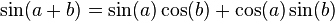
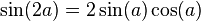
Ayrıca küresel trigonometride sinüs teoremini açıklamıştır:
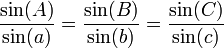
Ebu'l Vefa, Habeş el Hasib ve El Mervezi gibi önemli matematikçileri izleyerek tanjant ve sekant fonksiyonlarını tanımladı. Sekant kaşifi olarak genellikle Kopernik bilinirse de ünlü bilim tarihçilerinden Monte Candon ve Carra de Vaux'un araştırmaları sonucu bu buluşun Ebu'l Vefa'ya ait olduğu tespit edilmiştir.
Trigonometrinin yanında cebir ilmi üzerinde derinlemesine çalışmalarda bulunan Ebu'l Vefa o zamana dek bilinmeyen dördüncü dereceden denklemlerin çözümünü gerçekleştirdi.
Örneğin:
denklemini çözerken ve koniklerinin kesişmesinden istifade etti. Eski Yunanların ve Hintlerin çözemediği birçok problemi geometrik yollarla çözmeyi başardı.
Hârizmî
Hârizmî ya da tam adıyla Ebû Ca'fer Muhammed bin Mûsâ el-Hârizmî, matematik, gökbilim ve coğrafya alanlarında çalışmış Fars bilim adamı. Kökeni konusunda farklı düşünceler vardır. 780 yılında Harezm bölgesinin Hive şehrinde dünyaya gelmiştir. 850 yılında Bağdat'ta vefat etmiştir.
Cebir Alanındaki Çalışmaları
Cebir sözcüğü de Harezmi'nin "El’Kitab’ül-Muhtasar fi Hısab’il Cebri ve’l-Mukabele” (Cebir ve Denklem Hesabı Üzerine Özet Kitap) adlı eserinden gelmektedir. Bu eser aynı zamanda doğu ve batının ilk müstakil cebir kitabı olma özelliğini taşımaktadır.
Matematik alanındaki çalışmaları cebirin temelini oluşturmuştur. Bir dönem bulunduğu Hindistan’da sayıları ifade etmek için harfler ya da heceler yerine basamaklı sayı sisteminin kullanıldığını saptamıştır. Harezmî'nin bu konuda yazdığı kitabın Algoritmi de numero Indorum adıyla Latince'ye tercüme edilmesi sonucu, sembollerden oluşan bu sistem ve sıfır, 12. yüzyılda batı dünyasına sunulmuştur. Hesab-ül Cebir vel-Mukabele adlı kitabı, matematik tarihinde, birinci ve ikinci dereceden denklemlerin sistematik çözümlerinin yer aldığı ilk eserdir. Bu nedenle Harezmî (Diophantus ile birlikte) "cebirin babası" olarak da bilinir. İngilizce'deki "algebra" ve bunun Türkçe'deki karşılığı olan "cebir" sözcüğü, Harezmî'nin kitabındaki ikinci dereceden denklemleri çözme yöntemlerinden biri olan "el-cebr"den gelmektedir.
Harezmi sıfır rakamını ve x bilinmeyenini kullandığı bilinen ilk kişidir.
Battanî
Ebu Abdullah Muhammed bin Cabir bin Sinan er-Rekki es-Sabi el-Battani (858, Harran - 929, Samarra yakınlarındaki Kasr el-Cis kazası) Latince Albategnius, Albategni ya da Albatenius olarak bilinen, Arap astronom, astrolog ve matematikçidir. Şu anda Türkiye'de bulunan Urfa ilinin bir ilçesi olan Harran'da doğmuştur. Lakabı olan es-Sabi'dir fakat onun tam künyesi, bizi onun Müslüman olduğu sonucuna götürür.
Matematik
Battani, matematikte trigonometride günümüzde kullanılan formüller üretmiştir:
Ayrıca sin x = a cos x eşitliğini buldu, formül:
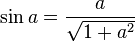
Battani,el-Mervezi'nin tanjant fikrini,tanjant ve kotanjant hesaplamaları amacıyla denklemler geliştirmek için konu hakkındaki matematiksel tablolarını derleyerek kullanmıştır.Bundan başka sekant ve kosekantın işteş fonksiyonalrını keşfetmiş ve O'nun gölgelerin tablosu olarak adlandırdığı,kosekantlar hakkındaki ilk mateamtiksel tabloyu,1'den 90'a kadar her bir dereceyi içerecek şekilde hazırlamıştır.
Vikipedi, özgür ansiklopedi
Son düzenleyen nötrino; 24 Nisan 2015 11:33
Sebep: İç başlık ve soru düzeni!!
