Dirac Denklemi Vikipedi, özgür ansiklopedi Adını İngiliz fizikçi Paul Dirac'tan alan dönülü ve göreli kuantum mekaniği denklemi,
şeklinde ifade edilebilir. Burada;m_0 : parçacığın durağan kütlesini,
c : ışık hızını, pμ : dörtmomentumu,
γμ : Dirac matrislerini
göstermektedir. Ayrıca Ψ, dört tane karmaşık sayıdan oluşan bir kolon matristir ve olasılığın dalga fonksiyonudur. Bu dört sayı da iki gruba ayrılır:
Buradaki Ψ + ve Ψ − , Dirac dönücüleri olarak adlandırılır ve her birinin farklı bir fiziksel anlamı vardır. Ψ + dönücüsü, pozitif enerjileri, Ψ − negatif enerjileri ifāde eder. Bunlar da ve
ve
olarak tanımlanır. ψ yukarı dönü ve φ aşağı dönü olarak anlam kazanır. Yani, dalga fonksiyonu;
şeklindedir. Serbest parçacık için Dirac denklemi Dırac denklemlerinde μ = 0 bileşenini ayırıp gerisi için i=1,2,3 indisini bırakırsak Dirac denklemi;
biçiminde yazılabilir. Dirac matrisleri; I, birim matris olmak üzere ve
ve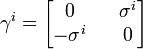
olarak Pauli matrisleri cinsinden yazılabilir. Bunlar yerine konunca Dirac denklemi,
biçimini alır. Matris çarpımı yapılırsa, çiftlenimli denklemler elde edilir: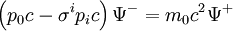
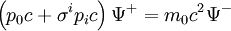
Bu özdeğer denklemlerini çözmek için, dönücülerden biri çekilip diğer denklemde yerine yazılabilir. Buradan, göreliliğin en önemli denklemlerinden biri elde edilir:
Burada p0c = E = mc2 ve  olduğundan ifade,
olduğundan ifade,
şeklindedir. Buradan E için pozitif ve negatif değerler gelir. Elektromanyetik alanda Dirac denklemi Denklemdeki dörtmomentum işlemcisine elektromanyetik potansiyeli dahil edersek: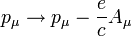
denklem,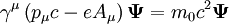
biçimine gelir. Buradaki Aμ, elektromanyetik dörtpotansiyeldir ve e elektriksel yüktür.
Gerçekçi ol imkansızı iste...