Cebrin, matematiğin öbür dallarına uygulanıp farklı nesnelerin belirli durumlarda tümüyle aynı özellikleri gösterdiğini ortaya koyması gerçekten çok ilgi çekicidir. Bunu açıklamak için, farklı matematiksel nesnelerle yapılan belirli bir işlemin sonuçlarını gösteren bir tablodan yararlanabiliriz. Örneğin, sayılar kendileriyle ve kendileri dışındaki öbür sayılarla çarpılarak bir tablo düzenlenebilir. Çarpim tablosu adı verilen bu tabloyu hepimiz biliriz. Bu tablo şöyle başlar:
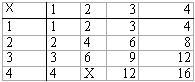
Bu tabloyu kullanarak, iki sayının, örneğin 3 ile 4'ün çarpımını bulabiliriz: 3'le başlayan satınn, üzerinde 4 yazılı sütunla kesiştiği yere bakınca gördüğümüz 12 sayısı 3 ile 4'ün çarpımıdır. Bu tabloda çarpmaya ilişkin ilgi çekici özellikler görülebilir. Örneğin, belirli bir sayının karesi olan 1,4,9, 16... gibi sayılar dışındaki bütün sayılar tabloda iki kez gözükmektedir. Bu, çarpmanın belirli bir özelliğinin sonucudur. Konumuza,
ab = ba
yazarak başlamıştık. Bu eşitlik, iki sayının çarpımında, çarpanların yer değiştirmesinin çarpımın sonucunu değiştirmeyeceğini anlatıyordu. Tabloda iki kez görülen aynı sayıdan biri axb'yi öbürü bxa'yı gösterir.
Şimdi de değişik bir çarpma yöntemini ele alalım. Yapacağımız çarpmada çıkacak sonucun birler basamağında bulunan sayı dışındaki bütün sayılarını atalım. Örneğin, 3x4=12 işleminde birler basamağındaki 2 sayısını alıp kalanını atalım;
Tabloya dikkat edersek ilginç bir sonuç görürüz. Elde ettiğimiz sonuçlar yalnızca 1,3,7 ve 9'dur. (Başka sayılar kullandığınızda da aynı sonucu alacağınızı düşünüyorsanız, 1, 2, 3, 4 sayılarını kullanarak benzer bir tablo düzenlemeyi deneyin.)
Bir başka örnek olarak, kare biçimindeki bir masanın çevresinde dört kişinin oturduğunu düşünelim. Harflerin cebirde her zaman sayıları temsil etmediğini biliyoruz. Bu örnekte, söz konusu dört kişinin yer değiştirmelerini harflerle gösterelim ve harflere aşağıda belirtilen anlamları verelim.
a Herkes yerinde kalıyor, s Herkes bir sola kayıyor, t Herkes bir sağa kayıyor, k Herkes karşısındakiyle yer değiştiriyor.
Bu durumda st ne anlama gelir?
Bu, s'yi t'nin izleyeceğini gösterir. Harflerin anlamını düşünürsek, herkes önce bir sola, sonra da bir sağa kayacak demektir. Bu durumda herkes başlangıçtaki yerine dönecek, demek ki aynı yerde kalmış olacaktır. Öyleyse,
st=a
yazabiliriz. Bu örnekteki işlemin tablosunu doldurmaya başlayalım:
k t
olur. İşlemi aynı
yöntemle sürdürürsek
3x7=1
7x9=3
3x9=7
sonuçlarını elde ederiz. Sonra 1,3,7 ve 9 sayıları için, çarpım tablosuna benzer bir tablo düzenleyelim:
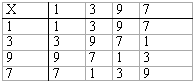
Önce s satırında kalan boşlukları dolduralım, sa, herkes bir sola kayacak ve sonra aynı yerde kalacak demektir. Bu ise, s'nin ifade ettiği hareketle aynı sonucu verir. Sonraki boşluğa geçelim: ss, herkes bir sola, sonra yeniden bir sola kayacak demektir. Bu ise, herkesin karşısındakiyle yer değiştirmesiyle aynı şeydir. Öyleyse ss'nin sonucu k'nin aynıdır. Gelelim sk'ye. Bu da, herkes bir sola kayacak ve sonra karşısındakiyle yer değiştirecek demektir. Bundan çıkacak sonuç ise t'nin, yani herkesin bir sağa kaymasının aynı olur. Elde ettiğimiz sonuçları tabloya işleyelim:
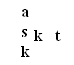
Aynı biçimde öbür boşlukları da doldurunca, tamamlanmış tablo şu görünümü alacaktır:
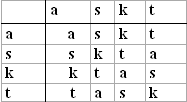
Şimdi konunun ilgi çekici bölümüne geliyoruz. Eğer, tablodaki her harfin yerine aşağıdaki gibi bir sayı koyarsak;
O zaman bu tablo, daha önce görmüş olduğumuz Tablo 1'e dönüşür. Bu iki tabloyu oluşturan iki işlem arasında gerçek hiçbir ilişki yoktur, ama bu iki sonuç kümesi tümüyle aynı özellikleri gösterir. Bu durumda, bunlar aynı cebirsel yapıya sahiptir denir.
Bu yapıyla ilgili olarak üç önemli özelliği belirtebiliriz:
1) Tablodaki her öğe başlangıçta ele alınan nesnelerden biridir. Örneğin Tablo 1'de, işleme 1,3,7 ve 9'la başladık ve tabloda bunlar dışında hiçbir şey elde etmedik.
2) Ötekilerle birleştiğinde onları etkilemeyen bir sayı ya da harf her zaman vardır. Buna etkisiz öğe denir. Tablo l'de, l'in bu nitelikte bir sayı olduğu açıkça görülüyor. 1 sayısı bildiğimiz basit aritmetikteki çarpma işleminde de böyledir; l'le çarpmak hiçbir şeyi değiştirmez. Tablo 2'de ise etkisiz öğe a'dır.
3) Her sayı ya da harf için, onun etkisini ortadan kaldıran, onun yaptığını tersine çeviren bir öğe vardır. Örneğin Tablo 2'de, s (sola kayma) t'nin (sağa kayma) etkisini ortadan kaldırır. Bunu biçiminde özetleriz. Bu eşitlik, "bir sola kaymak ve sonra bir sağa kaymak aynı yerde kalmaya eşdeğerdir" anlamını taşır, k kendi kendini etkisizleştirir; çünkü,
kk=a
dır. a da böyledir; çünkü,
aa=a
Bu üç özellik, matematikçilerin grup adını verdiği bir yapının belirgin özellikleridir. Şimdi, grup olmayan bir şeyin bu üç nokta çerçevesinde nasıl bir grup haline dönüştürülebileceğini görelim.
Yeniden doğal sayıları ele alalım ve bir toplama tablosu düzenlemek için onları birbiriyle toplayalım:

Bu tablo sonsuza dek uzayabilir; çünkü, doğal sayılar sonsuza gider. Hepsini sınaya-masak bile, iki doğal sayıyı topladığımızda gene bir doğal sayıya ulaşacağımız açık bir gerçektir. Öyleyse tablo aradığımız birinci özelliği taşıyor.
Bu toplama tablosunda acaba ikinci özellik var mı? Bu tabloda, ötekilere eklendiğinde etkisi olmayan hiçbir doğal sayı yoktur. Ama tablomuza sıfırı katarsak,
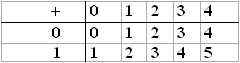
tablo ikinci özelliği de kazanır. Herhangi bir doğal sayıyı n ile gösterirsek, n+0=n olur.
Üçüncü özellikte durum biraz daha karmaşıktır. Bir doğal sayıyı, örneğin 5'i ele alalım. Tabloda, 5'in eklenmesinin etkisini ortadan kaldıracak başka bir doğal sayı yoktur. O nedenle,
x+5=0
st=a
denklemini de çözemeyiz.
Yeni bir tür sayı tanımlayarak bu güçlüğü giderebiliriz:
-5+5=0
Bu denklemde kullandığımız yeni sayı "eksi beş"tir. Böylece 5'e eklediğimiz zaman 0 elde edeceğimiz sayı 5 olur.
Her doğal sayıya karşılık olan bir "eksi" sayı vardır. Hepsinin birlikte oluşturduğu kümeye tamsayılar kümesi denir:
-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...
Cebrin çok ilgi çekici birçok başka uğraş alanı vardır. Matematiğin teorem adı verilen bazı genel yasalarını kanıtlamakta da cebir kullanılır.
MsXLabs.org & Temel Britannica