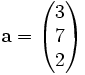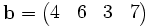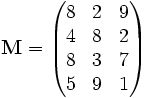Ziyaretçi
Cebir
cebir, aritmetik yöntemlerinin, simgelerle gösterilen değişken niceliklere uygulanmasına dayanan matematik dalı. Aritmetiğin genelleştirilmesi ve genişletilmesi niteliğindeki klasik cebirin yanı sıra, soyut matematiksel yapıların incelenmesini konu alan modern (soyut) cebir de günümüzde cebrin önemli bir dalını oluşturur.
Sponsorlu Bağlantılar
CEBİRİN KONUSU VE DALLARI
Aritmetik sayılara uygulanan, klasik cebir ise sayıların yanı sıra bilinmeyen ya da değeri belli olmayan sayıları temsil eden simgelere uygulanan işlemlere ilişkin kuralların bilimidir. Örneğin 2 ile 3ün toplamının 5 olduğu ya da 14ün 4e bölünmesiyle 3,5 elde edileceği aritmetiğin konusuna girer; oysa bütün a ve b sayıları için a+b - b+a olduğu bir cebir kuralıdır. Hem klasik, hem de soyut cebirin iki temel özelliği vardır: Cebir, yalnızca sonlu sayıda nicelik içeren ifadelerle ve sonlu sayıda adım içeren işlem dizileriyle ilgilidir. Örneğin,
1 4- x + x2 + x3 4- + xn = - ~ -X
1 x
bir cebir kuralıdır, ama
1 + x + x2 + x3 + + x" + = ^
1 x
kuralı cebirin alanı dışındadır. Cebirin ikinci temel özelliği soyut olmasıdır: Klasik cebirde işlemler soyut sayılara değil, sayıları temsil eden harflere uygulanır; modern cebirde ise, harfler, çok daha genel anlamda kullanılır ve soyut nesneleri temsil eder.
Klasik cebirin başlıca ilgi alamnı cebirsel denklem adı verilen ve yalnızca toplama, çıkarma, çarpma, bölme, üst ve kök alma işlemlerini içeren denklemlerin çözümü ve bu tür denklemlerin çözülmesi için gerekli olan sayı türlerinin tanımlanması oluşturur. Bu sayı türleri, 0,1,2,3,... gibi doğal sayıları; bunların negatiflerini; m ve « tamsayı (pozitif ya da negatif doğal sayı) olmak ve n=0 olmak üzere, m/n biçiminde tanımlanan rasyonel sayıları; bir doğru üzerindeki bütün noktalara karşılık gelen gerçek sayıları; a ile b gerçek sayılar olmak ve /=Vd olmak üzere a+ib biçiminde tanımlanan karmaşık sayıları içerir. Bu sayılara uygulanan işlemlere (örn. toplama, çarpma) ilişkin genel kuralların belirlenmesi de cebirin konusu içine girer.
Doğrusal (lineer) cebir, temel olarak, doğrusal denklemlerin çözümünü konu alan cebir dalıdır. Doğrusal denklemler, değişkenlerinin (bilinmeyenlerinin) derecesi lden büyük olmayan, bir başka deyişle değişkenlerin çarpımlarını ya da üstlü ifadelerini içermeyen denklemlerdir. Doğrusal terimi, x ve y değişkenlerini içeren böyle bir denklemin xy kartezyen düzlemindeki eğrisinin bir doğru olmasından kaynaklanmaktadır. Benzer biçimde, x, y ve z değişkenlerini içeren bir doğrusal denklem, üç boyutlu uzayda bir düzlem belirler; birlikte ele alınan böyle iki denklem ise uzayda iki düzlemin (eğer bu düzlemler paralel değilse) arakesiti olan bir doğruya karşılık gelir. Denklemdeki değişkenlerin sayısı 3ten büyükse denklemin geometrik bir karşılığı böyle yalın bir biçimde görülemez, çünkü fiziksel uzay üç boyutla sınırlıdır. Ama gene de bu benzetme sürdürülür; örneğin 4 değişkenli bir doğrusal denklemin 4 boyutlu uzayda bir aşırıdüzleme (hiperdüzlem) karşılık geldiğinden söz edilir; bu benzetme, sonlu olmak koşuluyla daha yüksek boyutlu uzaylar için de geçerlidir.
Doğrusal denklem sistemlerinin incelenmesi ve çözümünde matris ve vektörlerin kullanılması büyük kolaylık sağlar. Matris, satırlar ve sütunlar biçiminde dizilmiş sayılardan oluşan dikdörtgensel bir dizidir. Bir doğrusal denklem sisteminde, denklemlerdeki bilinmeyenlerin katsayılarından oluşan matris, sistemin özelliklerinin belirlenmesinde ve çözümünde temel önemdedir. Matrislere uygulanan işlemlere ilişkin kurallar matris cebrini oluşturur. Vektörle), başlangıçta, kuvvet ve hız gibi hem büyüklüğü, hem de doğrultusu bulunan fiziksel niceliklerin matematiksel betimlemesi olarak ortaya konmuştu. Vektörlerin bu fiziksel anlamından kaynaklanan hesaplama kuralları, vektör uzayı adı verilen kapalı vektör sistemlerinin oluşturulmasını sağladı. Bir vektör uzayında matrisler, doğrusal dönüşümler olarak bilinen özel fonksiyonlara karşılık gelirler. Sonlu boyutlu vektör uzaylarında doğrusal dönüşümlerin kuramı, doğrusal cebirin ana konusunu oluşturur. Bu kuram matrisler ve doğrusal denklemler kuramını da içerir.
19. yüzyılın ilk yarısında başlayan bir dizi gelişme sonucunda modern cebir oluştu. Klasik cebir, temelde, aritmetikte kullanılan sayıları ve bunlar üzerinde tanımlanmış toplama ve çarpma işlemlerini konu alıyordu (çıkarma ve bölme işlemleri, bu iki işlemin tersleri olarak düşünülebilir). Modem cebirin konusu ise cebirsel yapılardır. Cebirsel yapılar, belirli bir küme (öğeler topluluğu) üzerinde tanımlanmış bir ya da daha fazla işlemden oluşan ve belirli aksiyomlar içeren soyut sistemlerdir. Bir cebirsel yapının öğeleri sayılar olabileceği gibi, tümüyle soyut nesneler de olabilir. Eukleidesin aksiyomlarından farklı aksiyomlara dayanan yeni ve tutarlı geometrilerin oluşturulmasına benzer biçimde, klasik cebirin aksiyomlarından (örn.a.-vb = b +a)farklı aksiyomları temel alan yeni cebirler oluşturmak olanaklıdır. Örneğin, bir küme ile bu küme üzerinde tanımlanmış bir ikili işlemden oluşan bir sistem,
1) bu işlem birleşmeli ise,
2) kümede bu işleme göre bir birim öğe (etkisiz öğe) bulunuyorsa
3) kümenin her öğesinin bu işleme göre tersi varsa, grup olarak adlandırılır. Örneğin tamsayılar kümesi ve bu küme üzerinde tanımlanmış toplama işlemi bir grup oluşturur. Benzer biçimde, pozitif rasyonel sayılar kümesi ile çarpma işlemi de bir grup oluşturur. Bir eşkenar üçgeni, bulunduğu düzlem içinde kalmak koşuluyla, merkezi çevresinde 0°, 120° ve 240°lik açılarla döndürme, kümenin öğeleri olarak alınır; iki öğenin çarpım!, bir döndürmenin arkasından ikinci bir döndürme yapma olarak tanımlanırsa, bu sistemin yukardaki (1), (2) ve (3) koşullarını sağladığı, yani bir grup oluşturduğu görülür. Bir küpü, kendi üzerine oturacak biçimde, merkezi çevresinde döndürmenin 24 farklı biçiminden oluşan küme de bir grup oluşturur. 3 nesnenin 6 olanaklı permütasyonu, grup yapısına bir başka örnektir. Soyut cebirde, grup gibi bir tek işlem değil, iki farklı işlem içeren yapılar arasında halkalar ve cisimler sayılabilir. Örgüler ve belli özellikler içeren bir örgü türü olarak tanımlanabilen Boole cebiri de cebirsel yapılara bir başka örnek oluşturur.
Cebir, matematiğin en temel dalıdır; çünkü en basit aritmetik işlemlerden, en karmaşık diferansiyel ve integral hesaplarına kadar matematiğin bütün öteki dallarında uygulanan genel kuralların belirlenmesinde cebir kullanılır. Klasik cebir, aritmetik yöntemleri simgelerle gösterilen değişik niceliklere uygulayarak genelleştirir ve genişletir. Klasik cebrin yanı sıra, soyut matematiksel yapıları konu alan modern cebir vardır. Klasik cebrin aksiyomlarından farklı aksiyomları temel alan yeni cebir türleri de oluşturulabilir.
Klasik cebir aritmetik yöntemlerden hareket eder; onları genelleştirir ve genişletir. Örneğin iki sayının çarpımının, çarpanların yerleri değiştiğinde aynı kaldığını hepimiz biliriz.
3x4=4x3
Sayılar yerine harf kullanarak da bu çarpımı yazabiliriz. Sayılardan biri yerine a, öbürü yerine de b kullanırsak;
axb=bxa
olur. Bu eşitlik, "herhangi bir sayının başka herhangi bir sayı ile çarpımı, çarpanlar yer değiştirdiği zaman da hep aynı sonucu verir" kuralının kısa yoldan yazılmasıdır. Aslında bunu daha kısa;
ab=ba
olarak da yazabiliriz.
Sayılar yerine harf kullanıldığı zaman genellikle çarpma işareti kullanılmaz. Benzer biçimde, 2xc yerine 2c yazarız.
Harflerin sayıları temsil edecek biçimde kullanılmasında belirli kurallar geliştirilmiştir. Tek, çift ve doğal sayıları aşağıdaki biçimde sırayla yazalım.
Doğal sayılar= 1 2 3 4 5 6 7...
Çift sayılar= 2 4 6 8 10 12 14...
Tek sayılar= 1 3 5 7 9 11 13...
Bu çizelgeye bakınca ilk olarak, her çift sayının, kendi karşılığı olan doğal sayının iki katı; ikinci olarak da, her tek sayının, karşılığı olan çift sayıdan bir eksik olduğu görülür. "Herhangi bir doğal sayıyı temsil etmek için n harfini kullanırsak, çizelgede o doğal sayının karşılığı olan çift sayıyı, onun iki katı olduğu için 2n biçiminde yazabiliriz. Bu çift sayıya karşılık olan tek sayı da, onun bir eksiği olduğu için 2n1 biçiminde yazılabilir.
Doğal, tek ve çift sayılar arasındaki ilişkiyi harf kullanarak bu biçimde tanımlamış olmamız, n'inci tek ya da çift sayıyı kolayca bulabilmemizi sağlar. Örneğin, 25. tek sayıyı bilmek istersek, n yerine 25 yazarak sonucu kolayca buluruz.
2n-1=(2x25)-1=49
Soruyu tersinden de sorabiliriz. Örneğin, 101 sayısı tek sayılar sıralamasında kaçıncı sırada yer alır?
Bunu yanıtlamak için n'in hangi değerinin
2*1-1=101
eşitliğini sağladığını bulmaya çalışırız. Bunu çeşitli yollardan bulabiliriz; ama hangi yoldan olursa olsun bulunan sonuç
n=51
olacaktır. Demek ki, 101 sayısı 51. tek sayıdır.
Formüller ve Denklemler
Yukarıdaki 2n1 = 101 örneği basit bir denklemdir. Denklem iki niceliğin eşitliğini gösteren matematiksel bir anlatımdır.
Formül adı verilen genel bir denklemde bütün nicelikler yerine onları temsil eden harfler kullanılır. Örneğin bir dikdörtgenin alanını bulmak için uzunluğuyla (a) genişliğinin (£>), daha açık bir anlatımla uzunluğundaki birim sayısıyla genişliğindeki birim sayısının çarpıldığını biliriz. Bu, bir dikdörtgenin alanını [A] bulmaya yarayan formüldür (bak. Alan ve Hacim). Bu formül kısaca
A=ab
olarak yazılır.
Bir dikdörtgenin bazı büyüklüklerini bilirsek geri kalanlarını bulmak için bu formülü kullanabiliriz. Bir örnek verelim: Eğer bir dikdörtgenin alanının 42 cm2 ve uzunluğunun 7 cm olduğunu biliyorsak bu değerleri formüldeki yerlerine koyarak,
42=7 b
denklemini yazabiliriz. Bu denklemi çözerek fe'nin değeri bulunur. Buna benzer basit örneklerde denklem kolayca çözülür. Ama daha karmaşık başka denklemleri çözmek daha zor olabilir.
İkinci dereceden bir denklemi ele alalım:
x2+7x=25
"jr", "x'in karesi", başka bir deyişle "x'in temsil ettiği sayının kendisiyle çarpımı" demektir. Öyleyse denklemimizin anlamı şudur:
"Belirli bir sayıyı kendisiyle çarpıp buna aynı sayının 7 katını eklersek elde edeceğimiz sonuç 25 oluyor; acaba bu sayı kaçtır?"
Bu denklemi çözmenin birkaç yolu vardır. Önce x,in değerinin ne olabileceğini tahmin etmeye çalışalım; jc'in yerine 3 koyalım:
32+(7x3)=30
Sonuç 25'ten büyük çıktı. Öyleyse 2'yi deneyelim:
2:+(7x2)=18
Bu kez sonuç 25'ten küçük çıktı. Görülüyor ki x, 2 ile 3 arasında bir sayıdır. Bu kez x yerine 2,5 yazalım.
2,5: + (7x2,5) = 23,75
sonuç 25'e oldukça yakın, ama hâlâ 25'in altındadır. Bundan sonra deneyeceğimiz sayı 2,5 ile 3 arasında bir sayı olmalı. x yerine 2,6 yazarsak elde edeceğimiz sayı 24,96'dır. Bu 25'e çok yakın.bir sayıdır. Öyleyse x aşağı yukarı 2,6'ya eşittir.
Başka bir denklem türü iki bilinmeyenli denklemdir. 2x+y=3 gibi iki bilinmeyenli bir denklemde bilinmeyenlerden birinin alabileceği her gerçek değer için öbür bilinmeyenin de bir gerçek değeri vardır. Bu ikililerin oluşturduğu kümeye çözüm kümesi denir.
Başka bir denklem türü de denklem sistemleridir.
3x+y = x-3y = 7
gibi bir denklem sisteminde, iki bilinmeyenli iki ayrı denklemin birlikte çözümü gerekir. Bu denklem sisteminin çözümü her iki denklemin çözüm kümelerinin kesişimidir.
Cebirde harfler yalnızca sayıları temsil etmez. Matematikteki herhangi bir şey harflerle gösterilebilir.
Örneğin a ve b iki vektör olsun:
a+b=b+a
eşitliği, toplama işleminde, vektörlerin sıraları değiştirildiğinde sonucun değişmeyeceğini anlatır.
c=2a+b
ise, c vektörünün, a vektörünün iki katına b vektörünün eklenmesi sonucu elde edildiğini gösterir.
MsXLabs.org & Temel Britannica
Son düzenleyen Safi; 9 Nisan 2018 03:45

 Cebir
Cebir