Reed-Solomon hata düzeltme Vikipedi, özgür ansiklopedi Reed-Solomon hata düzeltme hata kodu düzelterek bu bir polinom veri kimden inşa oversampling çalışır.Bu polinom çeşitli noktalarda ve değerlendirilir bu değerler gönderir ya da kaydedildi.
Daha fazla gerekli olan polinom örnekleme üzerinde polinom yapar-belirlenir. aldığı "" noktalar çok doğru, alıcı bir "" birkaç kötü puan varlığını bile orijinal polinom kurtarabilirsiniz.
Reed-Solomon kodları ticari uygulamalar geniş bir yelpazede, kullanılmaktadır-ray diskler, veri iletimi teknolojilerinde DSL ve WiMAX gibi yayın sistemlerinde DVB ve ATSC gibi ve bilgisayar uygulamaları gibi RAID 6 sistemleri gibi.
Genel Bakış
Reed-Solomon kodları blok kodları vardır.
Bu giriş verisi sabit bir blok çıkış verileri sabit bir blok halinde işleme anlamına gelir.
ls.
En sık kullanılan R halinde-S kodunuzda (255, 223) - 223 Reed-Solomon giriş sembolleri (her sekiz bit uzunluğunda) 255 çıkış sembolleri olarak kodlanmış.
En çok AR-S hata kodu şemaları düzeltmek sistematik vardır.
Bu çıkış şifre bir kısmı orijinal forma giriş veri içeriyor demektir.
Bir Reed-sekiz bitlik Solomon sembol boyutu 255 semboller için en uzun şifre uzunluğu zorlar.- Standart (255, 223) Reed-Solomon kodunun 16 Reed her şifre olarak Solomon sembol hataları kadar düzeltmek yapabilir.
Her sembol aslında sekiz biti, bu kod hatası 16 öbekler kadar doğru olabilir.
The Reed-Solomon Kanunu, convolutional kodu gibi, şeffaf bir koddur.
.
Bu kanal sembolleri bir çizgi boyunca ters edilmiştir, yani kod çözücüleri yine çalışacağı anlamına gelir.
Sonuç orijinal verilerin tamamlayıcı olacaktır.
Ancak, Reed-Solomon kodu, kod kısaltılır (aşağıya bakınız) ve şeffaflık kaybeder.
Ya sıfır ya da kendisi tarafından doldurulması gereken bir kısaltılmış kodu gerekir bir "eksik" bit herhangi bir veri veya tamamlıyor olduğuna bağlı.
Eğer sembolleri ters olan (sonra sıfır doldurmak dolgu bir olanlarla ters gereken başka bir şekilde söylemek gerekirse.) Bu verileri bir anlamda (gerçek veya tamamlıyor) Reed önce çözülmesini yani zorunludur Bu nedenle -Solomon çözme.
Tanımı Genel Bakış
Bir Reed arkasındaki kilit fikir Solomon kod, veri kodlanmış öncelikle bir polinom olarak görüntülenir olmasıdır.
Kod cebir bir teoremi bu ülkelerin herhangi bir
K ayrı puan
benzersiz, en fazla, k derecede bir polinom belirlemek -
1 güvenmektedir.
Gönderici, bir sonlu alan üzerinde, bu K veri noktaları temsil eden bir ölçüde k - 1
polinom belirler.
Bu polinom sonra "kodlanmış" çeşitli noktalarda ve değerlendirme, ve bu değerleri gerçekte gönderilir bulunmaktadır.
Iletim sırasında, bazı değerlerin bozulabilir.
Bu nedenle, fazla
K noktaları aslında gönderilir.Gerekli değerleri doğru alınır, alıcı özgün polinom orijinal veri ne çözecektir.
Aynı anlamda bir bir polinom, orijinal eğri çizdim katsayıları kurtarmak için bir veri bloğu hatalardan bir dizi köprü olabilir geçmişte bir boşluk, bir Reed-Solomon kodunun interpolating bir eğri düzeltebilirsiniz.
Matematiksel formülasyon
Sonlu alan
F ve polinom halka
K [x Verdiği],
n ve
K gibi seçilmiş olsun bu
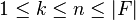
.
.Belirtilir K ve
n farklı öğeleri seçin
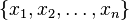
.
.
Daha sonra, codebook
C değerleri derece K az her K () üzerinde polinom değerlendirerek elde edilen
bu tuplets oluşturulan
her x I; yani,
 C
C a
[n, k, n - K
+ 1] kodu, diğer deyişle, bu uzunluğu n lineer kodu K
() K
boyut ve minimum
Hamming mesafesi n - K + 1 ile
üzerinde olmasıdır.
Bir
Reed-Solomon kodu yukarıdaki formun bir kod, ek şart tabi bu set
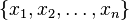
must be the set of all non-zero elements of the field F (and therefore, n = | F | − 1 ).
Tüm olmayan kurulum
alanında F sıfır unsurlar olmalıdır
(ve bu nedenle,
n = |
E | - 1).
Tarihçe .
Kod 1960 yılında Irving S. Reed ve Gustave Solomon, tarafından icat edilmiştir MIT Lincoln Laboratory üyeleri katkı sağlamıştır.
Ne zaman yazılmıştır, dijital teknoloji yeterli kavramını uygulamak için gelişmiş değildi.
Kitle SC kodlarının 1982'de ilk uygulama, ürünler imal kompakt disk, iki Interleaved SC kodları kullanılır oldu.
Büyük mesafe SC kodları için yeterli bir kod çözme algoritması Elwyn Berlekamp ve James Massey 1969 yılında geliştirilmiştir.
Bugün SC kodları sabit disk sürücüsü, DVD, telekomünikasyon, ve dijital yayın protokoller kullanılır.
Uygulamaları Veri depolama
Veri iletimi Posta kodlama
PostBar, MaxiCode, Datamatrix ve QR Code kullanmak Reed gibi Kağıt çubuğu kodları-Solomon hata düzeltme bile barkod bir kısmını bozuk doğru okuma sağlamak için kullanılır.
Uydu iletim
Geri Voyager uzay sondası tarafından gönderilen Reed bir önemli uygulama Solomon kodlama dijital fotoğraf kodlamak oldu.
.
Voyager (doğrudan dijital yayın) iletişim örneğin Reed-Solomon ML convolutional kodları bu yana çok derin uzay ve uydu yaygın hale gelmiştir bir uygulama ile birlikte kodlama tanıttı.


Olarak Şekil 1 ve 2, frekans bir yalıtılmış değer gösterildiği zaman alan bir düz dalga karşılık gelir.
Bu dalga boyu izole değeri yerini bağlıdır.
Tersine, rakamlar olarak 3 ve 4, zaman alan bir izole değeri frekans etki alanında düzgün bir dalga karşılık gösterilir.
.
Bir Reed In-Solomon kodu, frekans alan iki bölgede Şekil 5 deki gibi gösterilir: bölünmüştür sol (düşük frekans) uzunluğu K bölge ve sağ (yüksek frekans) uzunluğu n
bölgede -
K.
Bir veri kelime sonra sol bölge içine (derece bir polinom ve
K katsayıları ile ilgili en çok K yerleştirilmiştir
- 1) ise sağ bölge sıfır ile doldurulur.
Sonuç Fourier saat etki alanı içine, düşük frekanslarda sadece oluşan bir kod kelime ye dönüşmektedir.
Hata yoksa, ters Fourier tarafından frekans haline geri dönüşüm çözülemiyorsa bir şifre yazın.
Şimdi bir kod sözcük tek bir hata, Şekil 6'da gösterildiği içeren düşünün.
.
Frekans alanında bu hata The effect of sağ bölgede bir yumuşak, tek frekans dalga, hata ve
sendromu denir.
Hata konumu sendromu sinyalin frekansı belirleyerek belirlenir.
Benzer şekilde, iki veya daha fazla hata kodu kelime olarak tanıtıldı, bu sendromu sinyali iki veya daha fazla frekans oluşan, Şekil 7'de gösterilecek.
.
Hataları bununla belirlemek mümkündür.
Hata yerleri belirleme Sorun nedenle bulma sorunu için, n bir dizi - K değerleri
olan, bu değerleri çürümüş olabilir temel dalgaların en küçük ayarlamak verilen indirilmiştir.
e.
Bu dijital sinyal işleme gelen bu sorunun sıra en kısa doğrusal geribildirim kaydırma kaydı (LFSR) bulma sıra veya equivalently en az polinom ve kökleri, bulma eşdeğerdir bilinir.
Bu ikinci sorun ya inefficiently ve Berlekamp-Massey algoritması tarafından lineer denklemler bir sistem veya daha etkili bir şekilde çözümü ile çözülebilir.

Şekil 1

Şekil 2

Şekil 3

Şekil 4

Şekil 5

Şekil 6

Şekil 7
umarım bir yararı olur