Ziyaretçi
Arama
 Reed Solomon Kodları ve matlab uygulamaları hakkında bilgi verir misiniz?
Reed Solomon Kodları ve matlab uygulamaları hakkında bilgi verir misiniz?
Güncelleme: 18 Mart 2009 Gösterim: 11.079 Cevap: 7
Ziyaretçi
17 Mart 2009
Mesaj #1
Ziyaretçi
17 Mart 2009
Mesaj #2
Ziyaretçi
ENFORMASYON TEORİSİ
Sponsorlu Bağlantılar
O yıllardaki temel sorun iyi bir iletişimin nasıl olabileceği (daha sonra görüleceği gibi sinyal kanalda iletilirken bazı istenmeyen değişikliklere uğrar,daha iyi bir iletişimden kasıt bu istenmeyen değişimlerin kontrol altına alınabilmesidir) ve şifreleme idi.Bu amaçla yola çıkan Shannon önce iletişimin matematiksel bir modelini yapmayı düşündü ve böylece enformasyon teorisinin temelleri atılmış oldu.
Peki,şu anda enformasyon teorisi ne durumda? Teorinin kullanım alanı hızla genişleyip kısa sürede mühendisliğin dışına çıktı.Teori tamamen istatistiksel olduğu için isatistiksel fizik ile paralellikler gösterir ve belirsizlik kavramı ile kuantum fiziğine yaklaşır ama bundan daha fazlası da mevcut:
"I think of my lifetime in physics as divided into three periods. In the first period,extending from the begining of my career until the early 1950 s,I was in the grip of the idea that everything is particles.I was looking for ways to build all basic entities out of the lightest,most fundamental particles...
I call my second period everything is fields...
Now I m in the grip of a new vision,That everything is information ... the more I see possible fundamental roles for logic and information as the the bedrock of physical theory..."
John A. Wheeler (otobiyografisinden-1998)
Enformasyonu bu kadar önemli yapan ne? Şüphesiz, Wheeler in sözünü ettiği enformasyon ile Shannon un kastettiği enformasyon kavramsal olarak özdeş değil.Dolayısıyla en temel olan enformasyonun iyi bir tanımı yapılmalı.Şimdilik bundan uzağız ama işe enformasyon teorisinin temel kavramları ile başlayabiliriz...
Kavram Olarak Enformasyon
Enformasyon,iletişim sürecinin temel bir kavramı olarak gözümüze çarpıyor;ancak teoride bizim için önemli olan tam bir tanımdan çok enformasyonun ölçülebilir bir nicelik oluşu.
Enformasyon kaynağının sahip olduğu sonlu sayıdaki durumlarından birini dışarı vermesi (mesaj) sonucu,hedefe doğru bir enformasyon aktarım sürecinin başladığını düşünebiliriz.Kaynağın sonlu sayıdaki her bir durumunun ortaya çıkması (dışarı verilmesi) olasılıklarını tanımlarsak,bu olasılıklar yardımıyla açığa çıkan enformasyon miktarini belirtebiliriz. Enformasyon,iletişim sürecinin temel bir kavramı olarak gözümüze çarpıyor;ancak teoride bizim için önemli olan tam bir tanımdan çok enformasyonun ölçülebilir bir nicelik oluşu.
Genel Anlamda İletişim Sistemi
Genel anlamda iletişim sistemi 5 elemandan oluşur.
KAYNAK--->VERİCİ--->KANAL--->ALICI--->HEDEF
Enformasyon kaynağı;mesaj (ya da mesajlar dizisi) üreten herhangibir sistem olarak düşünülebilir. Üretilen bu mesaj,sistemin sahip olduğu sonlu sayıdaki durumlarından birinin dışarı verilmesidir.
Verici;kaynak tarafından üretilen mesajı, kanalda iletilebilecek biçime dönüştüren elemandır.Mesajın kanalda iletilebilecek biçimine sinyal adı verilir.
Kanal;sinyalin alıcıya iletildiği ortamdır.
Alıcı;sinyali,hedef tarafından algılanabilecek biçime dönüştüren elemandır.Alıcı;sinyali yeniden mesaj şekline dönüştürerek,vericinin yaptığı işlemin tersini yapmış olur.
Hedef;mesajın ulaştığı son noktadır.
En basit şekliyle iletişim sistemi;telefon aracılığı ile konuşan iki insan olarak düşünülebilir.Bu durumda enformasyon kaynağı,konuşan insan;verici,telefon ahizesi;kanal, telefon kabloları;alıcı,diğer taraftaki telefonun kulaklığı; hedef de diğer taraftaki insandır. Sinyalin kanalda iletimi sırasında -ortamın özelliklerinden dolayı- bazı değişimler oluşur.İstenmeyen bu değişimler gürültü olarak adlandırılır ve bu sebeble üretilen mesaj ile hedefin aldığı mesaj birbirinden farklı olur.
Genel Anlamda Enformasyon Teorisi ve Kavramları
Enformasyon teorisi -en temelde- kaynağın ürettiği mesajın enformasyon miktarı,kanalın iletebileceği maksimum enformasyon miktarı,iletim sırasında oluşan hatanın düzeltilmesi ve daha verimli bir iletim için kodlama (ya da şifreleme) yapılması gibi konularla ilgilenir.
Bunları yaparken,mesaj üretilme sürecinin, kaynağın sahip olduğu sonlu sayıdaki durumlardan birinin rastlantısal olarak dışarı verilmesi şeklinde olduğu kabul edilir.
Fakat bu;iki insanın telefonla iletişimi örneği için pek de yeterli değil.Çünkü kullanılan kelimelerdeki harfler tamamen rastlantısal olarak seçilmiyor.Mesajın anlam içeriği şimdilik göz ardı edilirse,daha iyi bir yaklaşım şöyle düşünülebilir:kullanılan harflerin seçimi tamamen rastlantısal değildir.(örneğin türkçede "a" harfi "v" harfine göre daha çok kullanılır,dolayısıyla bu harf daha büyük bir olasılıkla ortaya çıkar)Buna göre her harfin o dildeki kullanım sıklığı için ayrı olasılıklar atanır.Daha da ötesi;harflerin ard arda gelmeleri olasılıkları da atanabilir.(yine türkçede "a" harfinden sonra "k" harfinin gelme olasılığı,"a" harfinden sonra "g" harfinin gelme olasılığından daha fazladır)
Teoriye göre,kaynaktaki p olasılıklı bir durumun ortaya çıkması (mesaj oluşumu) log2(1/p) lik bir enformasyon oluşumudur.Burada logaritma 2 tabanındadır ve bu taban sadece birim seçimi ile ilgilidir.
Enformasyon miktarının bu tanımından şu sonuçlar çıkıyor:
*Ortaya çıkma olasılığı 1 olan bir durumun ortaya çıkması ile bir enformasyon oluşmaz.
*Oluşma olasılığı daha küçük olan durumun ortaya çıkması,büyük olana göre,daha büyük bir enformasyon miktari oluşturur.
En basit örnek olarak demir bir para ile yazı-tura atılması olayı düşünülebilir:Bu atış sonucunda paranın yazı ya da tura geldiğinin öğrenilmesi 1 bit lik bir enformasyon elde edilmesi anlamındadır.(yazı ya da tura gelme olasılığı 1/2)
Görüldüğü gibi kullanılan birim "bit" olarak adlandırılır.
Kaynağın entropi si,sahip olduğu durumların taşıdığı enformasyon miktarlarının ortalamasıdır.
å i pi.log2(1/pi)
Entropi kavramı ile belirsizlik kavramı bu teoride aynı amaç için kullanılır, yani entropi yerine belirsizlik de denilebilir. Entropinin (sistemdeki farklı durumların enformasyonları ortalamasının) -ya da belirsizliğin-;her durumun ortaya çıkma olasılığının eşit olduğu zaman,maksimum olduğu görülebilir.
Enformasyon'un Fizik ile İlişkisi...
Enformasyon teorisi ile fizik arasındaki olası bir ilişki nasıl olabilir?
Genel bir iletişim sisteminde kaynak yerine doğayı -ya da daha geniş anlamda evreni- ve hedef yerine de onu anlamaya calişan insanı koyarsak böyle bir ilişkinin kurulması olası gibi görünüyor.Bu durumda enformasyon için "bilgimizde değişiklik oluşturan şey" tanımı yapılabilir.Üstelik enformasyon teorisi yardımıyla bilgimizde meydana gelen değişikliği niceliksel olarak ifade edebiliriz.
Enformasyon teorisi enformasyonu niceliksel bir kavram olarak ele alıyordu ve onun için bir bağıntı veriyordu.Bu bağıntının yorumlanması sonucu ortaya çıkan iki sonuç şöyle yorumlanacaktır bu durumda:
*Ortaya çıkma olasılığı 1 olan bir durumun ortaya çıkması ile herhangibir enformasyon elde edilmez.Yani; iki yüzü de tura olan bir parayı attığımızda gelecek olanın tura olacağını zaten biliyoruzdur,bu atış sonucu bilgimizde herhangibir değişiklik oluşmaz.
*Ortaya çıkma olasılığı daha küçük olan bir durumun ortaya çıkması sonucu oluşan enformasyon miktari daha büyüktür (daha olası durumların enformasyonlarına göre) Yani; bir deney yaptığımızda eğer daha az beklediğimiz bir sonuç ile karşılaşırsak bilgimizdeki değişim daha büyük olur.
Basit bir örnek konuyu daha iyi açıklayacaktır. Elimizde sekiz siyah renkli kavanozun içinde reçel bulunduğunu düşünelim ve reçellerden sadece biri farklı bir çeşit olsun.Karşımızda bulunan birine -o kişi hangi kavanozdakininin farklı olduğunu biliyor- sorular sorarak farklı olanı bulmaya çalışalım.(Pek de heyecan verici bir oyun gibi görünmüyor))
Enformasyon teorisine göre doğru kavanozu bulduğumuzda 3 bit lik enformasyon elde etmiş olacağız.Çünkü 8 olası kavanozdan biri bizim aradığımızdır ve 1/8 bu kavanozu bulma olasılığımızdır.Bunun 2 tabanına göre logaritması -ki bu enformasyon miktarıdır- 3 dür. (şimdilik - işaretini göz önüne almıyoruz).Aynı zamanda enformasyon ortalaması da -entropi- 3 dür.Bu şöyle yorumlanabilir:eğer 3 soru sorarsak,cevaplarını aldığımızda doğru olanı bulmuş olacağız.Sorular iki cevaplı olmalıdır (evet/hayır) ve 3 ,bu soruların minimum sayısıdır. öyle ise sorular şu şekilde olabilir:
Kavanozları dörderli iki guruba ayırarak,farklı olan ilk gurubta mı? (cevap hayır olsun)
Ikinci gurup kavanozu yine iki ye ayırarak,farklı olan ilk gurubta mi?(cevap evet)
İlk gurubtaki iki kavanozu göz önüne alarak,farklı olan ilk kavanoz mu? (cevap hayır)
Öyle ise farklı olan kavanoz son ayırdığımız gurubtaki ikinci kavanozdur.
Fakat fizik ile olan ilişki reçel kavanozlarından daha derindir. İlki,enformasyon teorisindeki entropi ile istatistiksel fizikteki entropi kavramlarının matematiksel tanımlari zıt işaretlidir.Zamanın akış yönünü entropinin arttığı yön olarak algıladığımıza göre,entropi kavramı yerine enformasyon kavramı getirerek şöyle düşünebiliriz:
Bir sistem için zamanın akış yönünü,sistemin sahip olduğu enformasyonun azalış yönü olarak algılarız
Termodinamiğin ikinci yasasına göre,dengede olmayan sistem dengeye doğru evrilir ve bu sırada entropisi artar.Sistem bulunma olasılığının az olduğu durumlardan,bulunma olasılığının yüksek olduğu durumlara doğru gelişir.Enformasyon-entropi arasındaki ilişkiye göre dengede olmayan sistemin evrim yönü sahip olduğu enformasyonun azaldiği yöndür.
Bu noktada enformasyonun evrendeki en temel şey olduğu kabul edilip sistemlerin evrimi bu temelle açıklanabilir.(Wheeler in düşündüğünün bu olup olmadığını bilmiyorum) Temel parçaçıklar özdeş olduklarından,bu temel parçacıklardan oluşan yapılarda önemli olan,temel parçacıkların bir araya geliş düzenleridir yani enformasyon...Bu enformasyon elde edildiğinde aynı yapı başka bir yerde oluşturulabilir.(Temel parçacıkların özdeş olduğu ve her yerde bulunabilecekleri düşüncesiyle)
Ziyaretçi
17 Mart 2009
Mesaj #3
Ziyaretçi
Reed-Solomon; Haberleşmede kullanılan bir kodlama tekniğidir...
Koruma periyodu hücre degistirme gecikmelerinden ötürü
5s ile 20s arasında degisebilir.
“koruma_periyodu+çözücü_zamanı” ile hesaplanır.


Not: Bu konu Mühendislik Bilimleri (Bilgisayar Mühendisliği) ile ilgili olduğu için çok fazla kaynağa ulaşamadım...Bu kaynaklar da ödev raporu kaynaklarından...
Umarım işinize yarar.
Reed-Solomon Göndermede Hata
Düzeltim Kodları
Reed-solomon GHD kodları hataların düzeltilmesi için
çözümleyicide donanımsal düzeyde yapılandırma
gerektirir. Bundan dolayı oldukça karmasıktır.
Reed-Solomon GHD kodları hata düzeltmede
kullanıldıgında (n-k)/2nin herhangi bir
kombinasyonunu çözme yetenegine sahiptir. Diger
taraftan, Reed-Solomon kodları alıcı tarafında k tane
sembolü elde ettiginde (n-k) tane ekstra sembolü basarıyla
çözümleyebilir.
Reed-Solomon GHD kodları güçlü lineer hata düzeltim
kodlarıdır. Ancak paket düzeyinde kayıpların önlenmesi
için bazı kısıtlamalara sahiptir ve etkin degildir. Temel
kısıtlama sudur: Reed-solomon algoritması “Galois
Alanları” üzerinde çalısır. Her bir alan 8 bit (1 byte) ile Düzeltim Kodları
Reed-solomon GHD kodları hataların düzeltilmesi için
çözümleyicide donanımsal düzeyde yapılandırma
gerektirir. Bundan dolayı oldukça karmasıktır.
Reed-Solomon GHD kodları hata düzeltmede
kullanıldıgında (n-k)/2nin herhangi bir
kombinasyonunu çözme yetenegine sahiptir. Diger
taraftan, Reed-Solomon kodları alıcı tarafında k tane
sembolü elde ettiginde (n-k) tane ekstra sembolü basarıyla
çözümleyebilir.
Reed-Solomon GHD kodları güçlü lineer hata düzeltim
kodlarıdır. Ancak paket düzeyinde kayıpların önlenmesi
için bazı kısıtlamalara sahiptir ve etkin degildir. Temel
kısıtlama sudur: Reed-solomon algoritması “Galois
sınırlıdır. Özellikle gerçeklestirim yazılım tabanlı ise
ya da islemci gücü sınırlı ise uygulamak kolaydır.Reed-Solomon Gönderimde Hata
Düzeltim Kodları
Reed-Solomon kodları en iyi bilinen sistematik kodlardır.
Bu testte Reed-Solomonun internette yayınlanan ücretsiz
C++ kodları kullanılmıstır. Reed-Solomon kodunun
“Encoding ID” degeri 29 dur.
Reed-Solomon kodları lineer blok hata düzeltim
kodlarıdır. Reed-Solomon kodunun en büyük kısıtı
“Galois Alanları” üzerinde çalısıyor olmasıdır. Her bir
alan 8 bit (1 byte) ile sınırlıdır. Özellikle gerçeklestirim
yazılım tabanlı ise ya da islemci gücü sınırlı ise
uygulamak kolaydır.
Reed-Solomon kodunun temel özellikleri asagıdaki gidir:
Kaynak Kullanımı:
Reed-Solomon Göndermede Hata Düzeltim Kodunun ag
kaynaklarının ne kadarına ihtiyaç duydugu ile ilgilidir.
Bant genisliginin ne kadarını kullandıgı tabloda
verilmistir. [3]
Küçük dosya
indirimi(512
KB)
Büyük dosya
indirimi (3MB)
Düsük hata
oranı
13% 6%
Yüksek hata
oranı
30% 29%
Figür 2 – Hatasız veri almanın GHD koduna getirdigi
ek yük
Dosya indirimi için gereken bellek miktarı
Küçük dosyalarda (512 KB) 700KB hızında bellege
ihtiyaç duyulur. Büyük dosyalarda (3 MB) ise bu deger
4MB degerlerine çıkar. Bellek yönetim algoritmaları ile
bellek kullanımı düsürülebilir. Ancak bu standart degildir.
Esneklik
Farklı bit oranlarında çalısabilir. Reed-Solomon farklı
kaynak paket boyutlarını yönetebilir. (ag kaynaklarının
kullanımı, hesaplama karmasıklıgı ve performans degisir)
Reed-Solomon kodu farklı birer oranlarında (küçük
degerlerden 384 kbps degerine kadar olan aralık)
uygulanabilir
Reed-Solomon kodu esnek koruma periyoduna sahiptir.
Düzeltim Kodları
Reed-Solomon kodları en iyi bilinen sistematik kodlardır.
Bu testte Reed-Solomonun internette yayınlanan ücretsiz
C++ kodları kullanılmıstır. Reed-Solomon kodunun
“Encoding ID” degeri 29 dur.
Reed-Solomon kodları lineer blok hata düzeltim
kodlarıdır. Reed-Solomon kodunun en büyük kısıtı
“Galois Alanları” üzerinde çalısıyor olmasıdır. Her bir
alan 8 bit (1 byte) ile sınırlıdır. Özellikle gerçeklestirim
yazılım tabanlı ise ya da islemci gücü sınırlı ise
uygulamak kolaydır.
Reed-Solomon kodunun temel özellikleri asagıdaki gidir:
Kaynak Kullanımı:
Reed-Solomon Göndermede Hata Düzeltim Kodunun ag
kaynaklarının ne kadarına ihtiyaç duydugu ile ilgilidir.
Bant genisliginin ne kadarını kullandıgı tabloda
verilmistir. [3]
Küçük dosya
indirimi(512
KB)
Büyük dosya
indirimi (3MB)
Düsük hata
oranı
13% 6%
Yüksek hata
oranı
30% 29%
Figür 2 – Hatasız veri almanın GHD koduna getirdigi
ek yük
Dosya indirimi için gereken bellek miktarı
Küçük dosyalarda (512 KB) 700KB hızında bellege
ihtiyaç duyulur. Büyük dosyalarda (3 MB) ise bu deger
4MB degerlerine çıkar. Bellek yönetim algoritmaları ile
bellek kullanımı düsürülebilir. Ancak bu standart degildir.
Esneklik
Farklı bit oranlarında çalısabilir. Reed-Solomon farklı
kaynak paket boyutlarını yönetebilir. (ag kaynaklarının
kullanımı, hesaplama karmasıklıgı ve performans degisir)
Reed-Solomon kodu farklı birer oranlarında (küçük
degerlerden 384 kbps degerine kadar olan aralık)
uygulanabilir
Reed-Solomon kodu esnek koruma periyoduna sahiptir.
Koruma periyodu hücre degistirme gecikmelerinden ötürü
5s ile 20s arasında degisebilir.
Gecikme Süresi
“Tune in Delay” kavramı koruma periyodu ve çözücü
zamanının bir fonksiyonudur. “Tune in Delay”
zamanı, “koruma_periyodu+2” ile alttan sınırlı,
“2*koruma_periyodu” ile üstten sınırlıdır.
Gerçek zamanlı uygulamalarda gecikme
“Tune in Delay” kavramı koruma periyodu ve çözücü
zamanının bir fonksiyonudur. “Tune in Delay”
zamanı, “koruma_periyodu+2” ile alttan sınırlı,
“2*koruma_periyodu” ile üstten sınırlıdır.
Gerçek zamanlı uygulamalarda gecikme
“koruma_periyodu+çözücü_zamanı” ile hesaplanır.


Not: Bu konu Mühendislik Bilimleri (Bilgisayar Mühendisliği) ile ilgili olduğu için çok fazla kaynağa ulaşamadım...Bu kaynaklar da ödev raporu kaynaklarından...
Umarım işinize yarar.
Ziyaretçi
17 Mart 2009
Mesaj #4
Ziyaretçi
MATLAB UYGULAMALARI HAKKINDA...
MATLAB
Teknik Hesaplama Dili
MATLAB, veri görselleme, veri analizi ve erişimi ile nümerik hesaplama amaçlı yüksek seviyeli bir programlama dili ve etkileşimli bir platformdur.MATLAB kullanarak teknik hesaplama problemlerinizi,C/C++ ve Fortran gibi geleneksel programlama dillerine oranla daha hızlı çözümleyebilirsiniz...
Bütün dünyada teknoloji geliştiren tüm bilim adamları, şirketler ve araştırmacılar, çalışmalarını hızlandırmak, analiz ve metot geliştirme zamanlarını en aza indirgemek ve piyasaya daha gelişmiş ürünler sunmak için MATLAB kullanmaktadırlar
MATLAB, çok yönlü bir teknik hesaplama ortamı olarak matematiksel işlemler, veri analizi ve işlemesi, görselleştirme ve kuvvetli bir programlama dili yapısı gibi gereksinimlerin bir birleşimidir.
MATLAB’ın açık mimari yapısı ve kullanım kolaylığı; yapay sinir ağlarından güç sistemleri analizine, görüntü işlemeden finanssal modelleme araçlarına, kontrol sistemlerinden veri tabanı uygulamalarına, havacılık sistemlerinden otomotiv uygulamaları konularına ve çok daha fazla sayıdaki farklı alanlara yönelik özel ürünleri, kullanıcılara problemlerini en hızlı ve kolay yoldan çözebilme, algoritma hazırlama ve kişisel araçlar ve fonksiyonlar geliştirebilme imkanı tanır.
Neden MATLAB?
MATLAB, projelerdeki analiz ve geliştirme sürelerini azaltmakta, proje maliyetlerini indirmekte ve hemen her matematik-mühendislik-finans probleminde etkin çözümler sunabilmektedir. MATLAB hemen her konuya ilişkin çözümler sunabilen ürünlerini aynı platformda buluşturmaktadır. Böylelikle, mühendislerin aynı platformu kullanarak çalıştıkları projelerin farklı proseslerini zaman kaybına uğramadan işlemelerine, platform değiştirmeksizin etkin bir şekilde geliştirebilmelerine ve hayal gücünün sınırlarında diğer ürünler ile etkileşim içinde çalışma imkan tanır. Kullanıcılar, çok yönlü ve görsel MATLAB grafiksel kullanıcı arayüzünü, yazı yazma kolaylığındaki dil yapısını ve matematiksel-grafiksel hazır fonksiyon özelliklerini, C, Fortran veya diğer dil ve uygulamalara tercih etmektedir. MATLAB kullanılarak yapılan uygulamaların, C ve C++ dillerine dönüştürülebilir olması ve C, C++, Java veya Fortran’da hazırlanmış rutinlerin MATLAB’da kullanılabilir olması birçok araştırmacıyı MATLAB kullanmaya yöneltmiştir.


Önemli Özellikler
•Teknik hesaplama için yüksek seviyeli programlama dili
•Kod, dosya ve veri yönetimi için geliştirme ortamı
•İnceleme, tasarım ve problem çözümü için etkileşimli araçlar
•Doğrusal cebir, istatistik, Fourier analizi, filtreleme, eniyileme ve sayısal integral fonksiyonları
•Görselleştirme amaçlı 2 ve 3 boyutlu grafik fonksiyonları
•Özel amaçlı kullanıcı arayüzü geliştirme araçları
•MATLAB tabanlı algoritmaları C, C++, Fortran, Java, COM ve Microsoft Excel gibi dil ve uygulamalarla bütünleştirme araçları.
NOT: Aynı şekilde Bilgisayar Mühendisliği bölümü ile ilgili bir ders.
Matlab Uygulamaları ile ilgili bazı ders örnek verileri internette mevcut.Bilginize...
MATLAB
Teknik Hesaplama Dili
MATLAB, veri görselleme, veri analizi ve erişimi ile nümerik hesaplama amaçlı yüksek seviyeli bir programlama dili ve etkileşimli bir platformdur.MATLAB kullanarak teknik hesaplama problemlerinizi,C/C++ ve Fortran gibi geleneksel programlama dillerine oranla daha hızlı çözümleyebilirsiniz...
Bütün dünyada teknoloji geliştiren tüm bilim adamları, şirketler ve araştırmacılar, çalışmalarını hızlandırmak, analiz ve metot geliştirme zamanlarını en aza indirgemek ve piyasaya daha gelişmiş ürünler sunmak için MATLAB kullanmaktadırlar
MATLAB, çok yönlü bir teknik hesaplama ortamı olarak matematiksel işlemler, veri analizi ve işlemesi, görselleştirme ve kuvvetli bir programlama dili yapısı gibi gereksinimlerin bir birleşimidir.
MATLAB’ın açık mimari yapısı ve kullanım kolaylığı; yapay sinir ağlarından güç sistemleri analizine, görüntü işlemeden finanssal modelleme araçlarına, kontrol sistemlerinden veri tabanı uygulamalarına, havacılık sistemlerinden otomotiv uygulamaları konularına ve çok daha fazla sayıdaki farklı alanlara yönelik özel ürünleri, kullanıcılara problemlerini en hızlı ve kolay yoldan çözebilme, algoritma hazırlama ve kişisel araçlar ve fonksiyonlar geliştirebilme imkanı tanır.
Neden MATLAB?
MATLAB, projelerdeki analiz ve geliştirme sürelerini azaltmakta, proje maliyetlerini indirmekte ve hemen her matematik-mühendislik-finans probleminde etkin çözümler sunabilmektedir. MATLAB hemen her konuya ilişkin çözümler sunabilen ürünlerini aynı platformda buluşturmaktadır. Böylelikle, mühendislerin aynı platformu kullanarak çalıştıkları projelerin farklı proseslerini zaman kaybına uğramadan işlemelerine, platform değiştirmeksizin etkin bir şekilde geliştirebilmelerine ve hayal gücünün sınırlarında diğer ürünler ile etkileşim içinde çalışma imkan tanır. Kullanıcılar, çok yönlü ve görsel MATLAB grafiksel kullanıcı arayüzünü, yazı yazma kolaylığındaki dil yapısını ve matematiksel-grafiksel hazır fonksiyon özelliklerini, C, Fortran veya diğer dil ve uygulamalara tercih etmektedir. MATLAB kullanılarak yapılan uygulamaların, C ve C++ dillerine dönüştürülebilir olması ve C, C++, Java veya Fortran’da hazırlanmış rutinlerin MATLAB’da kullanılabilir olması birçok araştırmacıyı MATLAB kullanmaya yöneltmiştir.


Önemli Özellikler
•Teknik hesaplama için yüksek seviyeli programlama dili
•Kod, dosya ve veri yönetimi için geliştirme ortamı
•İnceleme, tasarım ve problem çözümü için etkileşimli araçlar
•Doğrusal cebir, istatistik, Fourier analizi, filtreleme, eniyileme ve sayısal integral fonksiyonları
•Görselleştirme amaçlı 2 ve 3 boyutlu grafik fonksiyonları
•Özel amaçlı kullanıcı arayüzü geliştirme araçları
•MATLAB tabanlı algoritmaları C, C++, Fortran, Java, COM ve Microsoft Excel gibi dil ve uygulamalarla bütünleştirme araçları.
NOT: Aynı şekilde Bilgisayar Mühendisliği bölümü ile ilgili bir ders.
Matlab Uygulamaları ile ilgili bazı ders örnek verileri internette mevcut.Bilginize...
17 Mart 2009
Mesaj #5
Reed-Solomon hata düzeltme
Vikipedi, özgür ansiklopedi
Reed-Solomon hata düzeltme hata kodu düzelterek bu bir polinom veri kimden inşa oversampling çalışır.Bu polinom çeşitli noktalarda ve değerlendirilir bu değerler gönderir ya da kaydedildi.
Daha fazla gerekli olan polinom örnekleme üzerinde polinom yapar-belirlenir. aldığı "" noktalar çok doğru, alıcı bir "" birkaç kötü puan varlığını bile orijinal polinom kurtarabilirsiniz.
Reed-Solomon kodları ticari uygulamalar geniş bir yelpazede, kullanılmaktadır-ray diskler, veri iletimi teknolojilerinde DSL ve WiMAX gibi yayın sistemlerinde DVB ve ATSC gibi ve bilgisayar uygulamaları gibi RAID 6 sistemleri gibi.
Genel Bakış
Reed-Solomon kodları blok kodları vardır.
Bu giriş verisi sabit bir blok çıkış verileri sabit bir blok halinde işleme anlamına gelir.
The Reed-Solomon Kanunu, convolutional kodu gibi, şeffaf bir koddur.
Sonuç orijinal verilerin tamamlayıcı olacaktır.
Ancak, Reed-Solomon kodu, kod kısaltılır (aşağıya bakınız) ve şeffaflık kaybeder.
Ya sıfır ya da kendisi tarafından doldurulması gereken bir kısaltılmış kodu gerekir bir "eksik" bit herhangi bir veri veya tamamlıyor olduğuna bağlı.
Eğer sembolleri ters olan (sonra sıfır doldurmak dolgu bir olanlarla ters gereken başka bir şekilde söylemek gerekirse.) Bu verileri bir anlamda (gerçek veya tamamlıyor) Reed önce çözülmesini yani zorunludur Bu nedenle -Solomon çözme.
Tanımı
Genel Bakış
Bir Reed arkasındaki kilit fikir Solomon kod, veri kodlanmış öncelikle bir polinom olarak görüntülenir olmasıdır.
Kod cebir bir teoremi bu ülkelerin herhangi bir K ayrı puan benzersiz, en fazla, k derecede bir polinom belirlemek - 1 güvenmektedir.
Gönderici, bir sonlu alan üzerinde, bu K veri noktaları temsil eden bir ölçüde k - 1 polinom belirler.
Bu polinom sonra "kodlanmış" çeşitli noktalarda ve değerlendirme, ve bu değerleri gerçekte gönderilir bulunmaktadır.
Iletim sırasında, bazı değerlerin bozulabilir.
Bu nedenle, fazla K noktaları aslında gönderilir.Gerekli değerleri doğru alınır, alıcı özgün polinom orijinal veri ne çözecektir.
Aynı anlamda bir bir polinom, orijinal eğri çizdim katsayıları kurtarmak için bir veri bloğu hatalardan bir dizi köprü olabilir geçmişte bir boşluk, bir Reed-Solomon kodunun interpolating bir eğri düzeltebilirsiniz.
Matematiksel formülasyon
Sonlu alan F ve polinom halka K [x Verdiği], n ve K gibi seçilmiş olsun bu 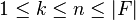
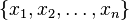
Daha sonra, codebook C değerleri derece K az her K () üzerinde polinom değerlendirerek elde edilen bu tuplets oluşturulan her x I; yani,
 C a [n, k, n - K + 1] kodu, diğer deyişle, bu uzunluğu n lineer kodu K () K boyut ve minimum Hamming mesafesi n - K + 1 ile üzerinde olmasıdır.
C a [n, k, n - K + 1] kodu, diğer deyişle, bu uzunluğu n lineer kodu K () K boyut ve minimum Hamming mesafesi n - K + 1 ile üzerinde olmasıdır.
Bir Reed-Solomon kodu yukarıdaki formun bir kod, ek şart tabi bu set 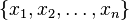
Tarihçe
Ne zaman yazılmıştır, dijital teknoloji yeterli kavramını uygulamak için gelişmiş değildi.
Kitle SC kodlarının 1982'de ilk uygulama, ürünler imal kompakt disk, iki Interleaved SC kodları kullanılır oldu.
Büyük mesafe SC kodları için yeterli bir kod çözme algoritması Elwyn Berlekamp ve James Massey 1969 yılında geliştirilmiştir.
Bugün SC kodları sabit disk sürücüsü, DVD, telekomünikasyon, ve dijital yayın protokoller kullanılır.
Uygulamaları
Veri depolama
Veri iletimi
Posta kodlama
PostBar, MaxiCode, Datamatrix ve QR Code kullanmak Reed gibi Kağıt çubuğu kodları-Solomon hata düzeltme bile barkod bir kısmını bozuk doğru okuma sağlamak için kullanılır.
Uydu iletim
Geri Voyager uzay sondası tarafından gönderilen Reed bir önemli uygulama Solomon kodlama dijital fotoğraf kodlamak oldu.


Olarak Şekil 1 ve 2, frekans bir yalıtılmış değer gösterildiği zaman alan bir düz dalga karşılık gelir.
Bu dalga boyu izole değeri yerini bağlıdır.
Tersine, rakamlar olarak 3 ve 4, zaman alan bir izole değeri frekans etki alanında düzgün bir dalga karşılık gösterilir.
Bir veri kelime sonra sol bölge içine (derece bir polinom ve K katsayıları ile ilgili en çok K yerleştirilmiştir - 1) ise sağ bölge sıfır ile doldurulur.
Sonuç Fourier saat etki alanı içine, düşük frekanslarda sadece oluşan bir kod kelime ye dönüşmektedir.
Hata yoksa, ters Fourier tarafından frekans haline geri dönüşüm çözülemiyorsa bir şifre yazın.
Şimdi bir kod sözcük tek bir hata, Şekil 6'da gösterildiği içeren düşünün.
Hata konumu sendromu sinyalin frekansı belirleyerek belirlenir.
Benzer şekilde, iki veya daha fazla hata kodu kelime olarak tanıtıldı, bu sendromu sinyali iki veya daha fazla frekans oluşan, Şekil 7'de gösterilecek.
Hata yerleri belirleme Sorun nedenle bulma sorunu için, n bir dizi - K değerleri olan, bu değerleri çürümüş olabilir temel dalgaların en küçük ayarlamak verilen indirilmiştir.
Bu ikinci sorun ya inefficiently ve Berlekamp-Massey algoritması tarafından lineer denklemler bir sistem veya daha etkili bir şekilde çözümü ile çözülebilir.

Şekil 1

Şekil 2

Şekil 3

Şekil 4

Şekil 5

Şekil 6

Şekil 7
umarım bir yararı olur
Vikipedi, özgür ansiklopedi
Reed-Solomon hata düzeltme hata kodu düzelterek bu bir polinom veri kimden inşa oversampling çalışır.Bu polinom çeşitli noktalarda ve değerlendirilir bu değerler gönderir ya da kaydedildi.
Genel Bakış
Reed-Solomon kodları blok kodları vardır.
ls.
En sık kullanılan R halinde-S kodunuzda (255, 223) - 223 Reed-Solomon giriş sembolleri (her sekiz bit uzunluğunda) 255 çıkış sembolleri olarak kodlanmış. - En çok AR-S hata kodu şemaları düzeltmek sistematik vardır.
Bu çıkış şifre bir kısmı orijinal forma giriş veri içeriyor demektir.
- Bir Reed-sekiz bitlik Solomon sembol boyutu 255 semboller için en uzun şifre uzunluğu zorlar.
- Standart (255, 223) Reed-Solomon kodunun 16 Reed her şifre olarak Solomon sembol hataları kadar düzeltmek yapabilir. Her sembol aslında sekiz biti, bu kod hatası 16 öbekler kadar doğru olabilir.
.
Bu kanal sembolleri bir çizgi boyunca ters edilmiştir, yani kod çözücüleri yine çalışacağı anlamına gelir. Sonuç orijinal verilerin tamamlayıcı olacaktır.
Ya sıfır ya da kendisi tarafından doldurulması gereken bir kısaltılmış kodu gerekir bir "eksik" bit herhangi bir veri veya tamamlıyor olduğuna bağlı.
Genel Bakış
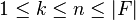
.
.Belirtilir K ve n farklı öğeleri seçin 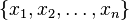
.
.  C a [n, k, n - K + 1] kodu, diğer deyişle, bu uzunluğu n lineer kodu K () K boyut ve minimum Hamming mesafesi n - K + 1 ile üzerinde olmasıdır.
C a [n, k, n - K + 1] kodu, diğer deyişle, bu uzunluğu n lineer kodu K () K boyut ve minimum Hamming mesafesi n - K + 1 ile üzerinde olmasıdır. 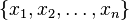
must be the set of all non-zero elements of the field F (and therefore, n = | F | − 1 ).
Tüm olmayan kurulum alanında F sıfır unsurlar olmalıdır (ve bu nedenle, n = | E | - 1). Tarihçe
.
Kod 1960 yılında Irving S. Reed ve Gustave Solomon, tarafından icat edilmiştir MIT Lincoln Laboratory üyeleri katkı sağlamıştır.Ne zaman yazılmıştır, dijital teknoloji yeterli kavramını uygulamak için gelişmiş değildi.
Uygulamaları
Veri depolama
Posta kodlama
Uydu iletim
.
Voyager (doğrudan dijital yayın) iletişim örneğin Reed-Solomon ML convolutional kodları bu yana çok derin uzay ve uydu yaygın hale gelmiştir bir uygulama ile birlikte kodlama tanıttı. 

.
Bir Reed In-Solomon kodu, frekans alan iki bölgede Şekil 5 deki gibi gösterilir: bölünmüştür sol (düşük frekans) uzunluğu K bölge ve sağ (yüksek frekans) uzunluğu n bölgede - K. .
Frekans alanında bu hata The effect of sağ bölgede bir yumuşak, tek frekans dalga, hata ve sendromu denir. .
Hataları bununla belirlemek mümkündür.e.
Bu dijital sinyal işleme gelen bu sorunun sıra en kısa doğrusal geribildirim kaydırma kaydı (LFSR) bulma sıra veya equivalently en az polinom ve kökleri, bulma eşdeğerdir bilinir. 
Şekil 1

Şekil 2

Şekil 3


Şekil 5

Şekil 6

Şekil 7
umarım bir yararı olur
Quo vadis?
Ziyaretçi
17 Mart 2009
Mesaj #6
17 Mart 2009
Mesaj #7
Ziyaretçi
18 Mart 2009
Mesaj #8
Ziyaretçi
Reed-Solomon ve Enformasyon hakkında sadece "bilgi verin" demiştiniz.Matlab uygulamaları için bir kaç kaynak buldum.Bunlara tek tek bakmanızı öneririm:
Matlab ile Grafik Uygulamaları
Matlab Uygulamaları
Matlab'ın Genel Çalışma Prensibi ( Bu konuda bilgi sahibi olmanız ve uygulamaları daha iyi anlama-geliştirmeniz açısından yararlı olacağına inandığım bir link)
Matlab için uygulama dosya örnekleri buldum.Ama bunlar Matlab platformunda açılıyor.Yani ben açamadım.Size linkini vereyim dosyaları indirin ama dediğim gibi Matlab Programlara arayüzünde açacaksınız.Matlab'ın yüklü olması gerekiyor.Buyrun KAYNAK
Matlab ile Grafik Uygulamaları
Matlab Uygulamaları
Matlab'ın Genel Çalışma Prensibi ( Bu konuda bilgi sahibi olmanız ve uygulamaları daha iyi anlama-geliştirmeniz açısından yararlı olacağına inandığım bir link)
Matlab için uygulama dosya örnekleri buldum.Ama bunlar Matlab platformunda açılıyor.Yani ben açamadım.Size linkini vereyim dosyaları indirin ama dediğim gibi Matlab Programlara arayüzünde açacaksınız.Matlab'ın yüklü olması gerekiyor.Buyrun KAYNAK
Benzer Konular
| 31 Ocak 2009 / Ziyaretçi Soru-Cevap |
| 16 Şubat 2016 / Ziyaretçi Soru-Cevap |
| 7 Ocak 2016 / doaNnn Taslak Konular |
| 15 Mart 2011 / Erdmen Soru-Cevap |
| 18 Nisan 2011 / Misafir Soru-Cevap |
| Kapat Saat: 09:35 Hoş Geldiniz Ziyaretçi
Benzer Konular
Son MesajlarYenile Yükleniyor... |


