Gerçel sayılar seti üzerinde, iki değişkenli (x ve y) iki boyutlu φ kuadratik formu şu formülle ifade edilir:


Kuadratik form aynı zamanda bir matris ifade ile de gösterilebilir:


Bu matris şeklinde ifadenin determinantinin açılması, daha önce diskriminat için verilen ifadeye, yani -1/4(b2 - 4ac) ifadesine eşittir. Bir geçen matris P kullanarak yapılan bir baz değişmesi bu determinatın değerinde değişme yapar. Daha detaylı bir açıklama ile, yeni baz için değer eski baz ile P determinantının karesinin çarpımına eşittir ve determinantın işareti değişmeden aynı kalmaktadır. Bu analizin incelenmesi daha ayrıntılı bir maddede yapılmaktadır.
Bunun için iki boyutlu kuadratik formları için üç tane farklı tanımlama yapılmaktadır. B bazında olan kuadratik formun dsiskriminantı, B bazındakı kuadratik forma bağlı olan matrisin determinatı olur. Daha onceki hale benzer bir açıklama ve hesaplama ile kuadratik formun diskriminantının b2 - 4ac. ifadesine esit olduğu tanımlanabilir. Sonra, kuadratik formun determinantına bağlı tek değişmez gibi, diskriminant da +1, 0 veya -1 değerleri alabilen determinant işareti olarak tanımlanır.
Diskriminant kuadratik formları üç tane değişik gruba ayırmaktadır. İki boyutta, kanonik bazda determinatın değerinin diskrimantı tanımlaması yapıldıktan sonra, eğer verilmis bir a degeri icin diskriminantın işareti pozitif ise, φ(x, y) = a değişebilirinin (x, y) noktalarının Ea ensamblı bir elipse karşıttır veye ensambl boştur. Eğer diskriminant sıfır ise, bu halde Ea bir parabol'a karşıt olur. Eğer diskriminant negatif ise, Ea bir hiperbol olur. Kuadratik formlar üç farklı şekilde konik seksiyon elde etmeye izin verir.

Herhangi bir derecede polinom

Bir polinom icin kok degerini diskriminant yardimi ile cikarma yontemi ikiden buyuk polinomlar icin generalize edilmemmistir. Fakat polinomun diskrimanti kavrami yine de kullanislidir. Dogrusal cebir icinde bir endomorfizim minimal polinomunda coklu koklerin mevcut bulunmasi endomorfizmin tabiatini degistir. Bu sekilde mevcudiyet diagonallestirme operasyonu imkansiz yapar. Bu aciklama rasyonel sayilarai da icine aldiginda, indirgenemiyen polinomlarin (yani faktorize edilemeyenler) coklu koklerinin bulunasi her turlu ahl icin imkansizdir. Bu hal tum haller icin gercek degildir. Galois teorisi icinde yapilan bu ayrim onemlidir ve sonuclar konfigirasyona bagli olarak degisik olabilir.


Örnekler

• Ikinci derece polinomlar icin ve matris notasyonu kullanarak su ifade ele gecirilir :

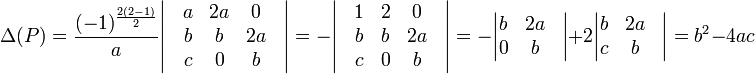
• Ucuncu derecede polinomlari icin genellikle bormalize edilmis polinom, yani ana diagonal elemanlarinin hepsi 1' e esit olan matrix, kullanilir ve su ifade ortaya cikar:

Bundan su formul cikartilir [1] :

Bu ifade epey karmasik gorunmektedir; fakat bunun bir uygun nedeni vardir. Geleneksel olarak bu karmasik ifade kullanilirsa yapilan ikamelerle su seklide bir polinom elde edilebilir ve bunun diskriminanti gayet basittir:



Gercel katsayili 3uncu derece polinom denklemi halinde, eger diskiriminant kesinlikle negatif ise denklemin uc tane ayri degerde gercel cozumu bulunur; eger determinant sifir ise uc tane birbirine cakisisan tek bir gercel degerde cozum vardir ve eger determinan kesinlikle pozitif ise tek bir gercel cozum nbulunupo diger iki tane cozum ise birbirlerine conjuge kompleks sayilardir.

• Elips egrisleri iki degiskenli ucuncu derece polinomlarin ozel bir seklinden ortaya cikarlar.

Elipsin en basit bir halinde denklem soyledir: y2 = x3 + ax + b Bunda a,b katsayilari gercel sayilardir. Bu halde diskiriminant soyle tanimlanir Δ = − 16(4a3 + 27b2).

Genel şekilde ifade

P dereceli polinom için genel diskriminant ifadesi şöyle tanımlanır:


ve bundan şu ortaya çıkar:

Diskriminant cebirsel tamsayılar halkası

Sayilar cebiri teorisi tanimi farkli gorunen bir diskriminant kavrami kullanir. Bu kavram bir kuadratik formdaki determinanta karsittir ve matamati halka A icin kullanilir. Her diskriminantin her iki tanimi da birbiriyle cok yakin olarak baglidirlar.
Eğer A halkasini (tumuyle relatiflerden olusan bir Z icin) Z[a] ile esit yapan bir cebirsel tamsayı a mevcutsa, a icin minimal polinom Z icindeki katsayilari aynen icerir. A'nin polinomlara gore tanimlanmis anlami ile cebirsel sayı teorisine gore halkanin diskrimanti anlamı ile tamamne esittir.