Kutupsal Koordinat Sistemi 3. Calculus (Analiz)
Kutupsal koordinatlar ile ifade edilmiş denklemlere kalkulus (diferansiyel ve integral hesaplamalar) uygulanabilir.
3.1. Diferansiyel hesaplama
Bir r(θ) kutupsal eğrisine herhangi bir noktasından teğet olan doğrunun Kartezyen eğimini bulmak için, eğri öncelikle parametrelere bağlı bir denklem sistemi ile tanımlanır: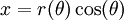
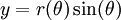
Sonra, bu denklemlerin θ'ya göre türevlerinin alınmasıyla şu denklemler elde edilir: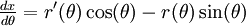
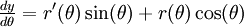
Birinci denklemin ikinciyle bölünmesi sonucunda da eğriye (r, r(θ)) noktasında teğet olan doğrunun Kartezyen eğimine ait denklem elde edilir: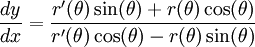
3.2. İntegral hesaplama
0 < b − a < 2π olmak üzere, r(θ) eğrisinin [a, b] kapalı aralığında kalan kısmının altında kalan alanı bulmak için, öncelikle eğri bir Riemann toplamı olarak tanımlanır.
- İlk olarak, [a, b] aralığı n kadar alt aralığa bölünür (burada n, isteğe bağlı seçilmiş pozitif bir tam sayıdır). Böylece, her alt aralığın uzunluğunu temsil eden Δθ, aralığın tüm uzunluğunun (b − a) alt aralık sayısına (n) bölümüne eşit olur.
- Her i = 1, 2, …, n alt aralığı için θi'nin alt aralığın orta noktası olduğu kabul edilir ve merkezi kutupta, yarıçapı r(θi) ve merkezî açısı Δθ olan birer sektör çizilir.
- Buna göre, çizilmiş her sektörün alanı şu denklemle verilebilir:
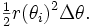
- Dolayısıyla, tüm sektörlerin toplam alanı da altta sunulan denklemle tanımlanır:
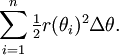
n alt aralıklarının sayısı ne kadar artarsa, söz konusu alanın ölçümü de gerçek alana o kadar çok yaklaşır. Böylece, [a, b] aralığındaki r(θ) eğrisinin altında kalan alan söyle tanımlanabilir: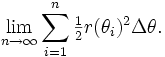
Bu ifade, aşağıdaki integralin Riemann toplamıdır: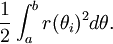
3.3. Vektörel hesaplamalar
Hesaplamalar, denklemlerin kutupsal koordinatlar içinde ifade edilmesi ile bu koordinatlarda uygulanabilir.
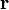, r ve θ t zamanına bağlı olmak üzere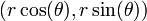 
pozisyonundaki vektör olsun;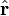 
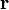, yönündeki birim vektör ve 
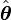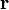, için uygun açılardaki birim vektör olsun. Konumun birinci ve ikinci türevleri şunlardır: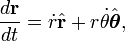
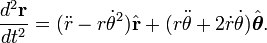
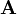eğri üzerindeki bir noktayı odak alarak çizilen çizginin süpürdüğü alan olarak alındığında, limit içinde 
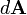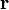, ve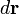 
tarafından şekillendirilmiş paralelkenar alanının yarısıdır,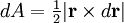
ve toplam alan 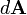'nın zamana göre integralinin alınması ile bulunur. Son düzenleyen Safi; 19 Aralık 2017 22:24
Tanrı varsa eğer, ruhumu kutsasın... Ruhum varsa eğer!
