Binom Açılımı ve Pascal Üçgeni!
Matematiksel işlemlerde çok sık karşılaşılan ifadelerden biri
(x+y)n. Genellikle bu ifadedeki x ve y herhangi iki sayı, n ise bir
tam sayıdır. Bu ifadenin eşitini bulmanın en basit yolu
n tane
(x+y) terimini birbiriyle çarpmaktır. Fakat n'nin büyük olduğu durumlarda bu işlemi yapmak çok uzun sürer. Binom açılımı olarak bilinen bir yöntem ile bu ifadenin eşiti çok daha kolay bir şekilde bulunabilir.
İfadenin eşiti açık olarak yazıldığı zaman bütün terimler
a+b=n olmak üzere,
x(a)y(b) şeklinde olacaktır. Bu terimlerin katsayılarına
binom katsayıları denir. Genel olarak binom açılımı şu şekilde ifade edilebilir:
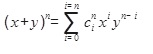
Bu ifadedeki katsayıların değeri
(!) faktöriyel işlemi olmak üzere, şöyle bulunabilir:
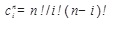
Örneğin n=2 olduğu zaman binom açılımı katsayıları 1, 2 ve 1 olur. Bu
(x+y)2 = x2 + 2xy + y2 anlamına gelir. n küçük olduğu zaman ifadenin eşitini bulmak için terimleri birbiriyle çarpmak da pratik bir yol olabilir, fakat n büyük olduğu zaman binom açılımını kullanmak çok daha kolaydır. Üstelik binom katsayılarını hesaplamak için yukarıdaki formülü kullanmaktan çok daha pratik bir yol var. Öncelikle birinci ve sonuncu katsayıların her zaman 1 olduğuna dikkat edin. Şimdi, yan kenarları alt alta yazılmış 1'lerden oluşan bir üçgen yapın. Daha sonra her satırda yan yana bulunan iki sayının altındaki satıra ve sayıların ortasına bu sayıların toplamını yazın.
Örneğin ikinci satırda iki tane 1 yan yana durduğu ve iki tane 1'in toplamı 2 olduğu için üçüncü satırın ortasına 2 yazın. Benzer şekilde, yukarıdan aşağıya doğru giderek üçgenin içini doldurmaya devam edin. Bu üçgenin her bir satırındaki sayıları incelediğiniz zaman sırasıyla belirli bir n değerine karşılık gelen tüm binom sayılarını bulacaksınız. Örneğin ikinci satırdaki 1, 1 sayıları
n=1'e karşılık gelen katsayılar, dördüncü satırdaki
1, 3, 3, 1 sayıları ise n=3'e karşılık gelen katsayılardır.
Pascal üçgeni olarak adlandırılan bu üçgeni kullanarak tüm binom katsayıları hesaplanabilir. Böylece
binom açılımı yapmak çok kolaylaşır.
Pascal üçgeninin pek çok ilginç özelliği var. Bunlardan biri Pascal üçgeninin
simetrik olmasıdır. Üçgenin ortasına
dikey bir simetri ekseni çizerseniz, bu simetriyi kolayca görebilirsiniz. Örneğin beşinci satırdaki 4'ler, altıncı satırdaki 10'lar ve yedinci satırdaki 15'ler bu eksene göre simetriktir.
Ayrıca satırlardaki sayıları yan yana tek bir sayı gibi okursanız 11'in kuvvetlerini bulursunuz. Bunun doğruluğu ise binom açılımında x=1, y=10 yazılarak görülebilir. Örneğin üçüncü satırdaki
1, 2, 1 sayıları bir araya getirildiğinde
11'in ikinci kuvveti olan
121 sayısını verir. Dördüncü satırdaki sayıların bir araya getirilmesi ile elde edilen 1331 sayısı ise 11'in üçüncü kuvvetidir. Katsayıların tek basamaklı olmadığı durumlar ise biraz daha karmaşıktır, fakat bu durumlarda da ufak bir çaba ile 11'in kuvvetleri bulunabilir.
Pascal üçgenini kullanarak
Fibonacci sayıları da bulunabilir. Fibonacci serisi
ilk iki terimi 1 olan bir seridir. Bu serinin elemanları olan Fibonacci sayıları ise kendinden önceki iki sayının toplamına eşittir. Örneğin bu serinin ilk birkaç elemanı şunlardır:
1, 1, 2, 3, 5, 8, 13, 21, 34. Bu serideki
8 sayısı kendinden önceki iki sayının
(3 ve 5) toplamıdır. Aynı şekilde 34 sayısı da 13'ün ve 21'in toplamıdır. Pascal üçgeninden
diyagonal parçalar alırsanız, her parçadaki sayıların toplamının Fibonacci sayılarını verdiğini göreceksiniz.
Pascal üçgeninde bulunabilecek diğer sayılar
üçgen sayılarıdır. Sadece noktalar kullanarak üçgen şekilleri yapmaya çalıştığınızı düşünün. Önce üçgenin tepesi için bir nokta, sonra bu noktanın altına üçgen oluşturacak şekilde iki nokta, daha sonra bu noktaların altına üç nokta, ... Her bir üçgeni yapmak için kullandığınız noktaların sayısı üçgen büyüdükçe 1, 3, 6, 10,... olarak devam eder. Bu sayıları Pascal üçgeninin ikinci
iç diyagonalinde bulabilirsiniz.
Bir başka özellik
Mersenne sayıları ile ilgilidir. 1'den ve kendisinden başka böleni olmayan sayılara asal sayılar denir. Mersenne sayıları ise
n bir
tam sayı olmak üzere,
2n-1'e eşit olan sayılardır ve n bir asal sayı olduğu zaman bu sayılar da birer asal sayı olur. Örneğin bir asal sayı olan 3'e karşılık gelen Mersenne sayısı 2(3)-1=7'dir. Benzer şekilde 5'e karşılık gelen Mersenne sayısı 2(5)-1=31'dir. Pascal üçgenini herhangi bir satırdan böler ve yukarıda kalan üçgendeki tüm sayıları toplarsanız Mersenne sayılarını verdiğini göreceksiniz.
Pascal üçgeninin tüm özellikleri ve daha başkaları binom katsayılarının değerleri kullanılarak ispatlanabilir. Pascal üçgeninin diğer bir özelliği satırlarındaki sayıların toplamının
2'nin kuvvetlerini vermesidir. Bunun doğruluğunu binom açılımında x ve y yerine 1 koyarak görebilirsiniz.
Kaynak: Bilimgenç / TÜBİTAK / PHYS