Ziyaretçi
Arama
 Logaritmada "e üzeri x" denilen tabloyu nasıl bulabilirim?
Logaritmada "e üzeri x" denilen tabloyu nasıl bulabilirim?
Güncelleme: 30 Kasım 2008 Gösterim: 21.178 Cevap: 1
Ziyaretçi
29 Kasım 2008
Mesaj #1
30 Kasım 2008
Mesaj #2
LOGARitaMA tabii logaritma,logaritmik tablolar
Logaritma VE özellikleri
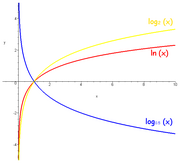
Logaritma: log10 (sarı),
ln (kırmızı) ve log½ (mavi)
Logaritma (Yunanca: λόγος (logos) = anlayış, ἀριθμός (aritmos) = sayı), 17. yüzyılın başında hesapları hızlandırmak için yapılan bir buluş. 300 yıldan daha uzun bir zaman, temel bir hesap metodu olmuştur. 19. yüzyılda masa hesap makinalarının doğuşu ve yirminci yüzyılda elektronik hesap makinalarının ortaya çıkışı, logaritmaya olan ihtiyacı azaltmıştır. Ancak logaritmik fonksiyonların teorik ve uygulamalı matematikte özel bir yeri vardır.
Logaritma, birbirinden habersiz çalışan iki kişi tarafından keşfedilmiştir. Bunlar; 1614'te İskoçyalı John Napier ve 1620'de İsviçreli Joost Bürgi'dir.
Logaritma üzerinde önemli çalışmaları olan bir Türk bilgini de Gelenbevi İsmail Efendidir. Kendisi büyük bir matematikçi olup, mantıkla da uğraşmıştır. 1730-1790 yıllarında yaşayan bu büyük alimin Logaritma Risalesi isimli çok açık, anlaşılır yazılmış bir eseri mevcuttur.
Logaritmayı açıklamak için 2·2·2= 8 ifadesine bakalım. Bu 2³ = 8 olarak kısaca yazılabilir. Bu örnekte 3, 8'in 2 tabanına göre logaritması denir.Buradan çıkan sonuç log28=3 'dur. Başka bir örnek, 2·2·2·2 = 16 ve 24= 16 yazılırsa, burada 4, 16'nın 2 tabanına göre logaritmasıdır.Yani log216=4 'tür. Genel olarak bx= N ifadesinde N'nin b tabanına göre logaritması, x'tir. Her ne kadar her pozitif sayı taban olarak kullanılırsa da genel olarak logaritma 10 ve e (yaklaşık, 2,718281828) tabanına göre hesaplanır.
Tabii logaritma
Eğer taban olarak yaklaşık 2,718281828 olan e sayısı alınırsa, bu logaritma tabii logaritma veya keşfeden John Napier'e izafeten Napier logaritması olarak da isimlendirilir. logeN yerine ln N ifadesi kullanılır. Mesela, ln 2= 0,6932'dir. Tabii logaritma genel olarak, ilmi kanunların ifadesinde sık sık ortaya çıkar.
Adi ve tabii logaritmalar birbirleri ile alakalı olup, tabii logaritma, adi logaritmaya 0,4343 sayısı ile çarparak çevrilebilir.
Adi ve tabii logaritmaların dışında herhangi pozitif bir reel sayı tabanına göre de logaritma kullanılır. Ancak negatif sayıların hiçbir tabana göre logaritmasının olmayacağı açıktır.log*altta iki var* 3.log*altta üç var* 4 bu işlemin sonucu nedir?
Denklemler


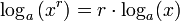

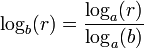
b = ax ifadesinde x değerini bulma işlemine logaritma denir.
ax = b ise x= logab dir.
Örnekler:
log3x = 5 ise x = 35 = 243'tür.
log6216 = x ise x = 3 bulunur.
Logaritma Fonksiyonunun Özellikleri
loga(m.n) = logam + logan dir.
(Çarpımın logaritması, çarpanların logaritmalarının toplamına eşittir.)
loga(m / n) = logam - logan dir.
(Bölümün logaritması, payın logaritmasından paydanın logaritmasının farkına eşittir.)
loga1 = 0.
(1 sayısının her tabandaki logaritması, a0=1 eşitliğinden dolayı sıfırdır.)
logaa = 1
(Tabanın logaritması, a1=a eşitliğinden dolayı 1 dir.)
logapn = n.logap
logap = logcp / logca dır.
(Taban Değiştirme Kuralı)
alogap = p
Örnekler:
log(2x + 12) = 1 + log(x - 2) denklemini sağlayan x değeri nedir?
log(2x + 12) = log10 + log(x - 2)
log(2x + 12) = log[10.(x - 2)]
2x + 12 = 10x - 20
x = 4 bulunur.
(log2x)2 - 6log2x + 8 = 0 denkleminin çözüm kümesi nedir?
log2x = t diyelim.
t2 - 6t + 8 = 0 olur.
Bu denklemin kökleri t1 = 2 ve t2 = 4 tür.
Buradan log2x = 2 veya log2x = 4 olur.
O halde x değerleri 22 = 4 ve 24 = 16 olup
Ç.K = {4,16} bulunur.
Logaritma VE özellikleri
Sponsorlu Bağlantılar

Logaritma: log10 (sarı),
ln (kırmızı) ve log½ (mavi)
Logaritma (Yunanca: λόγος (logos) = anlayış, ἀριθμός (aritmos) = sayı), 17. yüzyılın başında hesapları hızlandırmak için yapılan bir buluş. 300 yıldan daha uzun bir zaman, temel bir hesap metodu olmuştur. 19. yüzyılda masa hesap makinalarının doğuşu ve yirminci yüzyılda elektronik hesap makinalarının ortaya çıkışı, logaritmaya olan ihtiyacı azaltmıştır. Ancak logaritmik fonksiyonların teorik ve uygulamalı matematikte özel bir yeri vardır.
Logaritma, birbirinden habersiz çalışan iki kişi tarafından keşfedilmiştir. Bunlar; 1614'te İskoçyalı John Napier ve 1620'de İsviçreli Joost Bürgi'dir.
Logaritma üzerinde önemli çalışmaları olan bir Türk bilgini de Gelenbevi İsmail Efendidir. Kendisi büyük bir matematikçi olup, mantıkla da uğraşmıştır. 1730-1790 yıllarında yaşayan bu büyük alimin Logaritma Risalesi isimli çok açık, anlaşılır yazılmış bir eseri mevcuttur.
Logaritmayı açıklamak için 2·2·2= 8 ifadesine bakalım. Bu 2³ = 8 olarak kısaca yazılabilir. Bu örnekte 3, 8'in 2 tabanına göre logaritması denir.Buradan çıkan sonuç log28=3 'dur. Başka bir örnek, 2·2·2·2 = 16 ve 24= 16 yazılırsa, burada 4, 16'nın 2 tabanına göre logaritmasıdır.Yani log216=4 'tür. Genel olarak bx= N ifadesinde N'nin b tabanına göre logaritması, x'tir. Her ne kadar her pozitif sayı taban olarak kullanılırsa da genel olarak logaritma 10 ve e (yaklaşık, 2,718281828) tabanına göre hesaplanır.
Tabii logaritma
Eğer taban olarak yaklaşık 2,718281828 olan e sayısı alınırsa, bu logaritma tabii logaritma veya keşfeden John Napier'e izafeten Napier logaritması olarak da isimlendirilir. logeN yerine ln N ifadesi kullanılır. Mesela, ln 2= 0,6932'dir. Tabii logaritma genel olarak, ilmi kanunların ifadesinde sık sık ortaya çıkar.
Adi ve tabii logaritmalar birbirleri ile alakalı olup, tabii logaritma, adi logaritmaya 0,4343 sayısı ile çarparak çevrilebilir.
Adi ve tabii logaritmaların dışında herhangi pozitif bir reel sayı tabanına göre de logaritma kullanılır. Ancak negatif sayıların hiçbir tabana göre logaritmasının olmayacağı açıktır.log*altta iki var* 3.log*altta üç var* 4 bu işlemin sonucu nedir?
Denklemler


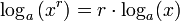

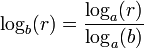
b = ax ifadesinde x değerini bulma işlemine logaritma denir.
ax = b ise x= logab dir.
Örnekler:
log3x = 5 ise x = 35 = 243'tür.
log6216 = x ise x = 3 bulunur.
Logaritma Fonksiyonunun Özellikleri
loga(m.n) = logam + logan dir.
(Çarpımın logaritması, çarpanların logaritmalarının toplamına eşittir.)
loga(m / n) = logam - logan dir.
(Bölümün logaritması, payın logaritmasından paydanın logaritmasının farkına eşittir.)
loga1 = 0.
(1 sayısının her tabandaki logaritması, a0=1 eşitliğinden dolayı sıfırdır.)
logaa = 1
(Tabanın logaritması, a1=a eşitliğinden dolayı 1 dir.)
logapn = n.logap
logap = logcp / logca dır.
(Taban Değiştirme Kuralı)
alogap = p
Örnekler:
log(2x + 12) = 1 + log(x - 2) denklemini sağlayan x değeri nedir?
log(2x + 12) = log10 + log(x - 2)
log(2x + 12) = log[10.(x - 2)]
2x + 12 = 10x - 20
x = 4 bulunur.
(log2x)2 - 6log2x + 8 = 0 denkleminin çözüm kümesi nedir?
log2x = t diyelim.
t2 - 6t + 8 = 0 olur.
Bu denklemin kökleri t1 = 2 ve t2 = 4 tür.
Buradan log2x = 2 veya log2x = 4 olur.
O halde x değerleri 22 = 4 ve 24 = 16 olup
Ç.K = {4,16} bulunur.
Quo vadis?
Benzer Konular
| 30 Kasım 2013 / Misafir Cevaplanmış |
| 15 Kasım 2012 / Ahmo22 Soru-Cevap |
| 18 Ekim 2011 / DreT45 Soru-Cevap |
| 15 Ekim 2009 / caganagur Soru-Cevap |
| Kapat Saat: 20:10 Hoş Geldiniz Ziyaretçi
Benzer Konular
Son MesajlarYenile Yükleniyor... |


