Ziyaretçi
pi sayısının gerçek şekli
Pi sayısı (π), bir dairenin çevresinin çapına bölümü ile elde edilen matematik sabiti. Pi sayısı ismini, Yunanca περίμετρον yani "çevre" sözcüğünün ilk harfi olan π harfinden alır. Bu harf Latin Alfabesi'nde Pİ ile sembolize edilir. Ayrıca pi sayısı Arşimet sabiti ve Ludolph sayısı olarak da bilinir.
Günlük kullanımda basitçe olarak ifade edilmesine rağmen gerçek değerini ifade etmek için periyodik olarak tekrar etmeyen sonsuz sayıda basamağa ihtiyaç vardır. İlk 65 basamağa kadar ondalık açılımı şöyledir:
olarak ifade edilmesine rağmen gerçek değerini ifade etmek için periyodik olarak tekrar etmeyen sonsuz sayıda basamağa ihtiyaç vardır. İlk 65 basamağa kadar ondalık açılımı şöyledir:
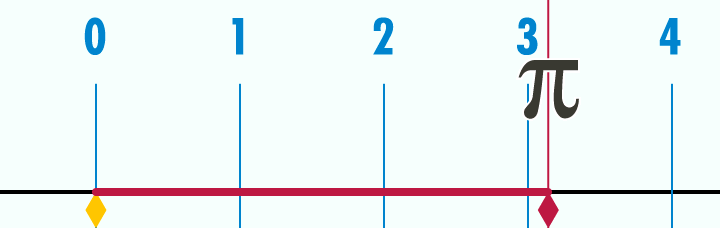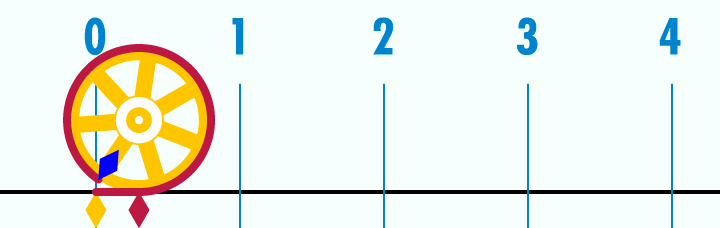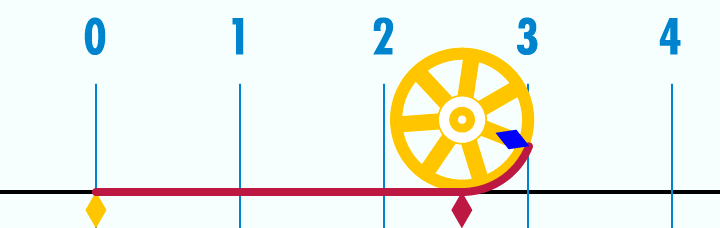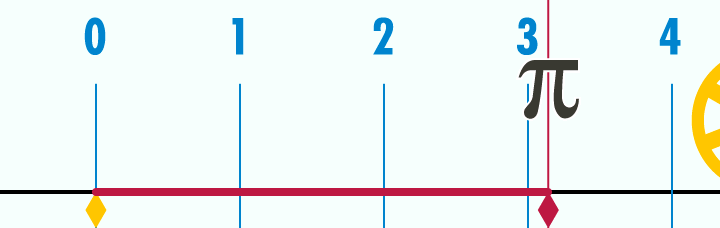
Çapı "1" olan Daire'nin çevresi "π" olur.
3, 14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 5923
Tarihçe
Babilliler'den beri Ortadoğu ve Akdeniz uygarlıklarının π sayısının varlığından haberdar oldukları bilinmektedir. Farklı antik uygarlıklar pi sayısı için farklı sayıları kullanmıştır. Örneğin MÖ 2000 yılı dolaylarında Babilliler π = 3 1/8, Antik Mısırlılar ise π = 256/81 yani yaklaşık 3,1605'i kullanmaktaydı. Yine de çok uzunca bir süre π'nin bir irrasyonel sayı olup olmadığı anlaşılamamıştır.
Pi sayısı Babiller, Eski Mısırlılar ve pek çok eski uygarlık tarafından biliniyordu. Onlar, tüm çemberlerin çevresinin çapına bölümünün sabit bir sayıya eşit olduğunu fark etmişlerdi. Bu sabit sayının bulunması artık çapı bilinen her çemberin çevresinin hesaplanmasına imkan tanıyordu. M.Ö. 2000 yılı civarında Babiller p sayısını 3 1/8 ya da 3,125 olarak kullanıyordu. Eski Yunanda karekök 10 ya da 3,162 sayısı kullanıldı. Arhimedes ise (M.Ö 287 – 212) 3 10/71 ve 3 1/7 sayısını pi sayısı olarak kullandı.
M.S. 500 yılı civarında p sayısı için 3,1415929 olarak kullanıyordu. 1424 yılında İran’da virgülden sonraki on altı basamağı doğru olarak biliniyordu. 1596 yılında Alman Ludolph van Ceulen, p nin virgülden sonraki yirmi basamağını hesapladı ve bu sayı Avrupa’da Ludolph sabiti olarak bilindi. O tarihten sonra pi sayısının virgülden sonraki milyarlarca basamağı hesaplanmıştır
Pi sayısı irrasyonel olmanın ötesinde ayrıca bir aşkın sayıdır da. Ferdinand von Lindemann tarafından 1882 senesinde ispatlanan bu gerçek, Pi'nin katsayıları tam sayı olan bir polinomun kökü olamayacağını ifade eder.
Pi sayısı matematikte çember ve yarı çapla doğrudan bağlantılı olmayan durumlarda da karşımıza çıkar. Mesela
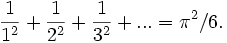
Pi, kültürel açıdan matematiksel sabitler içersinde en çok etki yaratanıdır. Bunu en basit nedenleri çok eskiden beri bilinmesi, çember gibi çok yaygın bir geometrik cisimle ilgili olması ise de bir başka nedeni de görünüşe göre bir kural izlemeyen ondalık açılımının insan aklını zorlayan kavranışıdır. Her ne kadar matematiksel açıdan π çok az bir gizem içerse de popüler kültürde bunun aksini işleyen eserler bolca mevcuttur. Ayrıca Eski Ahit'in bir bölümünde Pi sayısının değerinin 3 olduğu ima edildiğinden, kökten dinci hristiyanlar arasında π'nin değerinin okullarda 3 olarak öğretilmesini savunanlar da vardır.
π yi ilgilendiren birkaç formül
Aşağıdaki formüller, pi sayısını bilgisayar ortamında istenen duyarlılıkta hesaplamak için çeşitli gruplarca kullanılmıştır.

Günlük kullanımda basitçe
 olarak ifade edilmesine rağmen gerçek değerini ifade etmek için periyodik olarak tekrar etmeyen sonsuz sayıda basamağa ihtiyaç vardır. İlk 65 basamağa kadar ondalık açılımı şöyledir:
olarak ifade edilmesine rağmen gerçek değerini ifade etmek için periyodik olarak tekrar etmeyen sonsuz sayıda basamağa ihtiyaç vardır. İlk 65 basamağa kadar ondalık açılımı şöyledir:Sponsorlu Baglantilar

Çapı "1" olan Daire'nin çevresi "π" olur.
3, 14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 5923
Tarihçe
Babilliler'den beri Ortadoğu ve Akdeniz uygarlıklarının π sayısının varlığından haberdar oldukları bilinmektedir. Farklı antik uygarlıklar pi sayısı için farklı sayıları kullanmıştır. Örneğin MÖ 2000 yılı dolaylarında Babilliler π = 3 1/8, Antik Mısırlılar ise π = 256/81 yani yaklaşık 3,1605'i kullanmaktaydı. Yine de çok uzunca bir süre π'nin bir irrasyonel sayı olup olmadığı anlaşılamamıştır.
Pi sayısı Babiller, Eski Mısırlılar ve pek çok eski uygarlık tarafından biliniyordu. Onlar, tüm çemberlerin çevresinin çapına bölümünün sabit bir sayıya eşit olduğunu fark etmişlerdi. Bu sabit sayının bulunması artık çapı bilinen her çemberin çevresinin hesaplanmasına imkan tanıyordu. M.Ö. 2000 yılı civarında Babiller p sayısını 3 1/8 ya da 3,125 olarak kullanıyordu. Eski Yunanda karekök 10 ya da 3,162 sayısı kullanıldı. Arhimedes ise (M.Ö 287 – 212) 3 10/71 ve 3 1/7 sayısını pi sayısı olarak kullandı.
M.S. 500 yılı civarında p sayısı için 3,1415929 olarak kullanıyordu. 1424 yılında İran’da virgülden sonraki on altı basamağı doğru olarak biliniyordu. 1596 yılında Alman Ludolph van Ceulen, p nin virgülden sonraki yirmi basamağını hesapladı ve bu sayı Avrupa’da Ludolph sabiti olarak bilindi. O tarihten sonra pi sayısının virgülden sonraki milyarlarca basamağı hesaplanmıştır
Pi sayısı irrasyonel olmanın ötesinde ayrıca bir aşkın sayıdır da. Ferdinand von Lindemann tarafından 1882 senesinde ispatlanan bu gerçek, Pi'nin katsayıları tam sayı olan bir polinomun kökü olamayacağını ifade eder.
Pi sayısı matematikte çember ve yarı çapla doğrudan bağlantılı olmayan durumlarda da karşımıza çıkar. Mesela
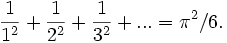
Pi, kültürel açıdan matematiksel sabitler içersinde en çok etki yaratanıdır. Bunu en basit nedenleri çok eskiden beri bilinmesi, çember gibi çok yaygın bir geometrik cisimle ilgili olması ise de bir başka nedeni de görünüşe göre bir kural izlemeyen ondalık açılımının insan aklını zorlayan kavranışıdır. Her ne kadar matematiksel açıdan π çok az bir gizem içerse de popüler kültürde bunun aksini işleyen eserler bolca mevcuttur. Ayrıca Eski Ahit'in bir bölümünde Pi sayısının değerinin 3 olduğu ima edildiğinden, kökten dinci hristiyanlar arasında π'nin değerinin okullarda 3 olarak öğretilmesini savunanlar da vardır.
π yi ilgilendiren birkaç formül
Aşağıdaki formüller, pi sayısını bilgisayar ortamında istenen duyarlılıkta hesaplamak için çeşitli gruplarca kullanılmıştır.
- Euler'in bir formülü:


 Pi sayısının gerçek şekli nasıldır?
Pi sayısının gerçek şekli nasıldır?


