Geometrik Medyan
Ziyaretçi
Geometrik Medyan
İstatistik bilim dalında geometrik medyan betimsel istatistik alanında bir merkezsel konum ölçüsü olarak ve çıkarımsal istatistik alanında önemli bir konum parametre kestirimicisi olarak kullanılır. Geometrik medyan bir Euclid-tipi uzayda bulunan aralıklı set halindeki örneklem noktaları, bu noktalar arasındaki uzaklıkların toplamını en küçük (minimum) yapan bir nokta olarak tanımlanır. Tek boyutlu veri serisi içinde veri noktaları arasında uzaklıkları minimum yapma özelligi olan medyanın, çok boyutlu veri uzayında karşıtı olup, bir çokdeğişirli merkezsel konum ölçüsü olur. Geometrik medyan için kullanılan diğer adlar Fermat-Weber noktası veya 1-medyan olur.
Geometrik medyan yöneylem araştırması, Endüstri Mühendisliği alanlarında bulunan ve pratikte çok önemi olan standart üretim ve dağıtım kuruluşu konumlanma problemi için kullanılan yaklaşımlardan en popüleridir; çünkü geometrik medyan noktasında konumlanma taşıma maliyetlerini en küçük yapan bir noktadır.
Tanınım
Geometrik madyan için matematik biçimde tanımlama şöyle yapılır:
Her biri
içinde m tane nokta olan 
seti verilmiş olsun. Bu halde geometrik medyan matematiksel olarak şöyle tanımlanır:
Geometrik Medyan
Burada argmin verilen toplamanın hangi argümanlara göre minimumunun bulunduğunu gösterir. Bu halde bütün xi noktalarina giden Euclid-tipi uzaklıklarının toplamını minimum yapacak bir başlangıç noktası olan y noktasıdır.
Özellikler
Kavram olarak anlaşılması oldukça kolay olan geometrik medyan bulmak için kullanabilcek bir matematik formül daha mevcut değildir. Geometrik medyana benzer olan, ve her örneklem noktasının uzaklık karelerinin toplamını minimum yapan sentroid veya kütle merkezi için basit bir formül bulunmaktadır. Ama uzaklık toplamını minimize edecek geometrik medyan için bunun imkânsız oldugu, yani sadece aritmetiksel işlemler ve kinci kökler hesapları kullanılmasını öneren bir matematik formülün bulunmasinin genel olarak mümkün olamayacağı, isbatlanmıştır.
Cebirsel sekilde bir formulun bulunamasina ragmen, sayisal yaklasimlar kullanilarak yinelemeli surecle, her bir yinelemede daha geometrik medyan icin cok uygun yaklasik degerler bulunabilir. Bu tip yordamlarin kullanilmasi temelinde bulunan gercek uzakliklarin toplaminin bir konveks fonksiyon olamasidir cunku her orneklem veri noktasina uzaklik konveks oldugu icin, konveks fonksiyonlarin toplaminin da konveksdir. Boylece her bir cozum asamasinda uzakliklarin toplamini azaltan bir yordam bir yoresel optimum noktasina takilip kalmamaktadir.
Geometrik medyan bulmak icin kullanilan bir yineleme ile yaklasik cozum bulma islemine Weiszfeld'in algoritmasi adi verilmektedir. ve bu yinelemeli tekrar agirliklanmis en kucuk kareler yonteminin bir degisik seklidir.
Bose ve arkadaslari {2003) bu probleme bir yaklasik optimal cozum degeri bulmak icin daha komplike geometrik optimizasyon yontemlerinin kullanilmasini onermektedirler.
Örtük formül
Eğer y tüm diğer verilmiş noktalar olan xj lerden belirgin olarak farkı ise, ynin geometrik medyan olması ancak ve ancak şu ifadeyi tatmin ederse mümkündür:
Bu ise Weiszfeld'in algoritmasının yakın benzeri olan şu ifadeyle aynıdır:
Eğer y verilmiş olan noktaların bazılarına eşit ise, o halde ynin geometrik medyan olması ancak ve ancak
koşuluna uyan uj vektörlerinin bulunması ile mümkün olur. Burada xj ≠ y için
ve xj = y için
xj = y olur.
Geometrik Ortalama
Geometrik ortalama, birim değerlerinin (gözlem sonuçlarının) birbirleriyle çarpımlarının, n birim sayısı olmak üzere, n inci dereceden köküne denir.
Birim değerleri x1, x2, ... , xn gibi gösterilirse geometrik ortalama aşağıdaki gibi yazılır:
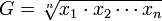İstatistiksel araştırmalarda gözlem sonuçları arasındaki oransal (nispî) farkların mutlak farklardan daha önemli olduğu durumlarda geometrik ortalamaya başvurulur. Diğer bir ifade ile gözlem sonuçlarının her biri bir önceki gözlem sonucuna bağlı olarak değişiyorsa ve bu değişmenin hızı saptanmak istenirse geometrik ortalama sağlıklı sonuçlar verir. Geometrik ortalama kısaca G harfi ile gösterilir.
Geometrik ortalama bulmak veri değerlerinin pozitif olmasi gerekir. Eğer tek bir veri değeri sıfır ise geometrik ortalama anlamsız olur.
Sponsorlu Bağlantılar
Geometrik medyan yöneylem araştırması, Endüstri Mühendisliği alanlarında bulunan ve pratikte çok önemi olan standart üretim ve dağıtım kuruluşu konumlanma problemi için kullanılan yaklaşımlardan en popüleridir; çünkü geometrik medyan noktasında konumlanma taşıma maliyetlerini en küçük yapan bir noktadır.
Tanınım
Geometrik madyan için matematik biçimde tanımlama şöyle yapılır:
Her biri
içinde m tane nokta olan seti verilmiş olsun. Bu halde geometrik medyan matematiksel olarak şöyle tanımlanır:Geometrik Medyan
Burada argmin verilen toplamanın hangi argümanlara göre minimumunun bulunduğunu gösterir. Bu halde bütün xi noktalarina giden Euclid-tipi uzaklıklarının toplamını minimum yapacak bir başlangıç noktası olan y noktasıdır.
Özellikler
- Tek boyutlu uzayda, geometrik medyan medyan ile çakışır. Buna neden tekdeğişirli medyanın da veri noktalarından medyana uzaklıklarının toplamının minimum olmasıdır.
- Eğer noktalar doğrudaşlık (İngilizce:collinearity) özelliğine sahip değillerse, geometrik medyan tanınıma uyan yegane tek bir noktadır.
- Geometrik medyan Euclid tipi (cevirme ve devretme gibi) [benzerlik donusumleri]]ne esit degisme gosterir. Bu demektir ki geometrik medyana uygulanan benzerlik donusumu ile elde edilen sonuc ile once veri serisine ayni donusumu uygulayip sonra donusumlu serilerin geometrik medyani alma sonucuyla aynidir. Bu ozellik geometrik medayanin sadece nokta ciftlerine gore tanimlanmasi nedeninden ve orneklem veri serisinin temsil edildigi ortogonal Kartezyen koordinat sistemine bagli olmamasindan ortaya cikar. Buna karsilik, bir coklu degsisrli veri dizisi kollanilarak elde edilen coklu-medyan genellikle rotasyon donusumunden etkilenmekte ve koordinat sitemi secimine cok guclu olarak bagli olmaktadir.
- Geometrik medyan için çöküntü noktası 0,5 olarak hesaplanmıştır. Bu demektir ki eğer örneklem veri serisinin yarısı keyfi bir şekilde bozulmuşlarsa, geometrik medyan bu halde bile, bozuk olmayan verilerin ortaya çıkarabileceği merkezsel konum noktasının bir güçlü kestirimi olacaktır.
- Üç nokta için: Eğer bir üçgenin herhangi bir açısı 120°den daha büyük ise, geometrik medyan bu açının başlangıç köşe noktasıdır. Eğer tüm açılar 10&geg;den daha az ise, geometrik medyan üçgenin içinde öyle bir noktadır ki tüm üç çift noktaya 120°lik bir açı kurulabilirse, bu nokta üç noktaya kurulmuş olan bir üçgenin Fermat noktası olarak da bilinir.
- Dört aynı-düzeysel noktalar için: Eger bir nokta diğer üç noktadan kurulmuş olan bir üçgenin içinde ise bu nokta geometrik medyandır. Aksi halde, noktalar bir konveks dörtgen kurarlar ve geometrik medyan bu dörtgenin köşegenlerinin kesişme noktasıdır. Bu nokta dört köşe noktasının Radon noktası olarak bilinir.
Kavram olarak anlaşılması oldukça kolay olan geometrik medyan bulmak için kullanabilcek bir matematik formül daha mevcut değildir. Geometrik medyana benzer olan, ve her örneklem noktasının uzaklık karelerinin toplamını minimum yapan sentroid veya kütle merkezi için basit bir formül bulunmaktadır. Ama uzaklık toplamını minimize edecek geometrik medyan için bunun imkânsız oldugu, yani sadece aritmetiksel işlemler ve kinci kökler hesapları kullanılmasını öneren bir matematik formülün bulunmasinin genel olarak mümkün olamayacağı, isbatlanmıştır.
Cebirsel sekilde bir formulun bulunamasina ragmen, sayisal yaklasimlar kullanilarak yinelemeli surecle, her bir yinelemede daha geometrik medyan icin cok uygun yaklasik degerler bulunabilir. Bu tip yordamlarin kullanilmasi temelinde bulunan gercek uzakliklarin toplaminin bir konveks fonksiyon olamasidir cunku her orneklem veri noktasina uzaklik konveks oldugu icin, konveks fonksiyonlarin toplaminin da konveksdir. Boylece her bir cozum asamasinda uzakliklarin toplamini azaltan bir yordam bir yoresel optimum noktasina takilip kalmamaktadir.
Geometrik medyan bulmak icin kullanilan bir yineleme ile yaklasik cozum bulma islemine Weiszfeld'in algoritmasi adi verilmektedir. ve bu yinelemeli tekrar agirliklanmis en kucuk kareler yonteminin bir degisik seklidir.
Bose ve arkadaslari {2003) bu probleme bir yaklasik optimal cozum degeri bulmak icin daha komplike geometrik optimizasyon yontemlerinin kullanilmasini onermektedirler.
Örtük formül
Eğer y tüm diğer verilmiş noktalar olan xj lerden belirgin olarak farkı ise, ynin geometrik medyan olması ancak ve ancak şu ifadeyi tatmin ederse mümkündür:
Bu ise Weiszfeld'in algoritmasının yakın benzeri olan şu ifadeyle aynıdır:
Eğer y verilmiş olan noktaların bazılarına eşit ise, o halde ynin geometrik medyan olması ancak ve ancak
koşuluna uyan uj vektörlerinin bulunması ile mümkün olur. Burada xj ≠ y için
ve xj = y için
xj = y olur.
Geometrik Ortalama
Geometrik ortalama, birim değerlerinin (gözlem sonuçlarının) birbirleriyle çarpımlarının, n birim sayısı olmak üzere, n inci dereceden köküne denir.
Birim değerleri x1, x2, ... , xn gibi gösterilirse geometrik ortalama aşağıdaki gibi yazılır:
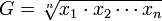İstatistiksel araştırmalarda gözlem sonuçları arasındaki oransal (nispî) farkların mutlak farklardan daha önemli olduğu durumlarda geometrik ortalamaya başvurulur. Diğer bir ifade ile gözlem sonuçlarının her biri bir önceki gözlem sonucuna bağlı olarak değişiyorsa ve bu değişmenin hızı saptanmak istenirse geometrik ortalama sağlıklı sonuçlar verir. Geometrik ortalama kısaca G harfi ile gösterilir.Geometrik ortalama bulmak veri değerlerinin pozitif olmasi gerekir. Eğer tek bir veri değeri sıfır ise geometrik ortalama anlamsız olur.
