Ziyaretçi
Dik açılı üçgenin özellikleri nedir?
DİK ÜÇGEN
DİK AÇILI ÜÇGEN
Bir açısının ölçüsü 90° olan üçgene dik üçgen denir. Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir. Hipotenüs üçgenin daima en uzun kenarıdır. şekilde, m(A) = 90° [BC] kenarı hipotenüs
[AB] ve [AC] kenarları dik kenarlardır.
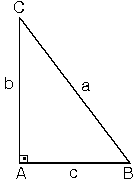
DİK ÜÇGENİN ÇEVRESİNİN HESAPLAMASI
ÇEVRE (P)= A+B+C
DİK ÜÇGENİN ALANIN HESAPLAMASI
DEVAMI Dik üçgen ve özellikleri
DİK AÇILI ÜÇGEN
Sponsorlu Bağlantılar
[AB] ve [AC] kenarları dik kenarlardır.
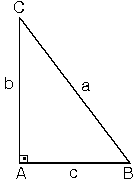
DİK ÜÇGENİN ÇEVRESİNİN HESAPLAMASI
ÇEVRE (P)= A+B+C
DİK ÜÇGENİN ALANIN HESAPLAMASI
DEVAMI Dik üçgen ve özellikleri
Son düzenleyen Safi; 11 Nisan 2017 06:22

 Dik açılı üçgenin özellikleri nedir?
Dik açılı üçgenin özellikleri nedir?
