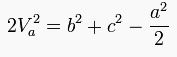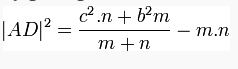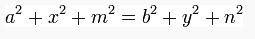Ziyaretçi
Üçgenlerin çevre ve alanı nasıl hesaplanır?
Üçgen
Sponsorlu Baglantilar
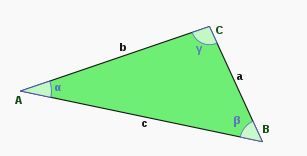
Herhangi bir üçgen.
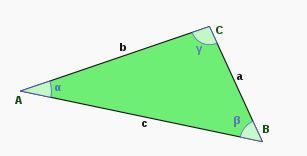
Bir üçgen, düzlemde birbirine doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimidir.
Düzlem geometrisinin temel şekillerinden biridir. Bir üçgenin üç köşesi ve bu köşeleri birleştiren, doğru parçalarından oluşan üç kenarı vardır. Bir Üçgenin iç açılarının toplamı 180° dış açılarının toplamı 360°'dir.
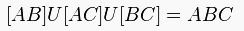
Burada;
A, B, C noktaları üçgenin köşeleri ve
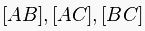 doğru parçaları üçgenin kenarlarıdır.
doğru parçaları üçgenin kenarlarıdır. 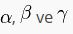 üçgenin iç açılarıdır.
üçgenin iç açılarıdır.Matematiksel tanım
Yukarıda anlatılan biçimiyle (Öklit düzleminde) üçgen, [Riemann geometrisinde daha genel bir nesnenin özel bir durumudur. X bir Riemann uzayı ve A, B, C, bu uzayın birbirine doğrusal olmayan üç noktası olsun. Bu üç noktanın her bir çifti arasında birer kesel (jeodezik) seçilsin. Bu üç keselin birleşimine ABC üçgeni denir. Örneğin, bir Riemann yüzeyi olarak dünya yüzeyinde, kuzey kutbundan 0 meridyeniyle ekvatora, ekvator boyunca 90. doğu meridyenine, bu meridyen boyunca geri kuzey kutbuna çıkan eğri, bir üçgen oluşturur. Bu üçgenin iç açıları toplamı 270°'dir.
Üçgenin açıları
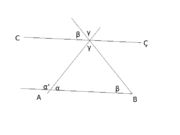
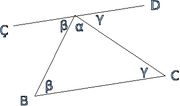
Üçgenin dış açıları
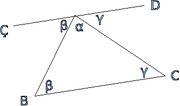
Üçgenin iç açıları toplamının 180 derece olduğunun ispatı
BAC, ABC ve ACB üçgenin içaçılarıdır.
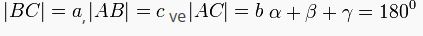
- Üçgenin iç açıları toplamı 180 derecedir.
- Üçgende bir dış açı, kendisine komşu olmayan iki iç açının toplamına eşittir.
Üçgenlerin türleri
Üçgenler, kendilerini oluşturan parçaların (köşe, kenar, açılar vb.) aynı düzlemde olup olmadığına göre sınıflandırılabilir. Eğer üçgenin tamamı tek bir düzlemdeyse düzlemsel, diğer durumlarda da örneğin küresel ya da hiperbolik üçgen terimleri kullanılır.
Kenarlarına Göre
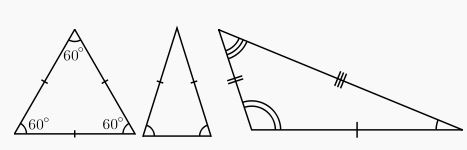
Eşkenar, İkizkenar, Çeşitkenar
İkizkenar Üçgen
İki kenarı eşit olan üçgenlerdir. Ayrıca iki açısı birbirine eşitir. Eşit olmayan kenara indirilen dikme hem açıortay hem kenarortay özelliği gösterir.
Dar Açılı Üçgen
Açıları 90 dereceden küçük olan üçgenlere denir.
Dik Üçgen
Dik Üçgen Bir açısı dik (90°) olan üçgenlerdir. Bu üçgenlerde yükseklik dik kenarlardan biridir. En uzun kenarına hipotenüs denir.
Geniş Açılı Üçgen
Açılarından biri 90°den geniş olan üçgenlerdir. Sadece bir tek kenarı geniş açı olabilir. Tabana ait yükseklik tabanın uzantısı ile kesişir.
Pisagor bağıntısı
Bir dik üçgenin dik kenarlarına 'a' ve 'b' dersek hipotenüs'ün karesi bu kenarların uzunluklarının karelerinin toplamına eşittir. Buna Pisagor Teoremi denir. Yani:
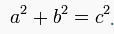
Alan Hesaplaması
Kenardan Yararlanma
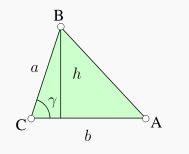
Alan hesaplaması
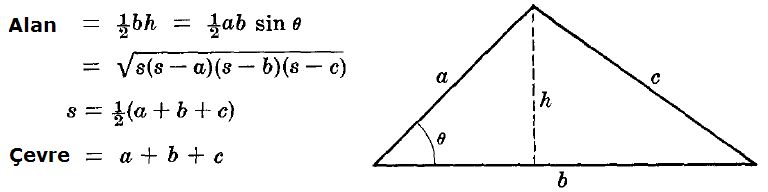
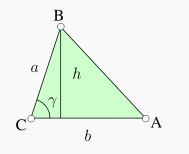
Bir üçgenin alanı taban ve tabana ait yüksekliğin çarpımının yarısıdır:
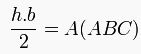 ayrıcaınızın başıyla da ölçebilirsiniz.
ayrıcaınızın başıyla da ölçebilirsiniz.Açıdan Yararlanma
Bir üçgenin alanı herhangi iki kenarını ile aralarında kalan açının sinüsünün çarpımının yarısıdır.
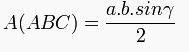
Heron Yöntemi
Çevre uzunluğuna '2u',' dersek alan:
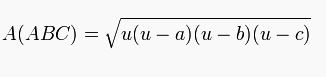
Kosinüs Teoremi
Kosinüs teoremi
Herhangi bir üçgende a, b, c kenarlarını alalım. a ve b arasında kalan açı da alfa(α) olsun. c kenarını bulmak için kullanılacak formül:
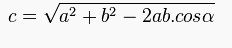
Üçgende yardımcı elemanlar
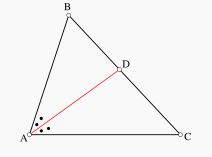
Açıortay
Açıortay
Bir açıyı iki eş açıya bölen doğru veya doğru parçasına açıortay denir. Açıortayların kesiştiği nokta, üçgenin içteğet çemberinin merkezidir..
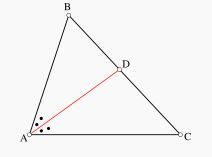
Açıortay

Kenarortay
Kenarortay
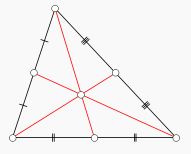
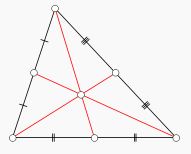
Kenarortaylar ve ağırlık merkezi
Bir üçgende bir köşeden karşısındaki kenara uzatılan doğru bu kenarı iki eş parçaya bölüyorsa buna kenarortay denir.Bir üçgende kenarortayların kesiştiği noktaya ağırlık merkezi denir. G harfi ile gösterilir.
Ağırlık merkezi, bir kenarortayı 2n ve n olarak böler. Yani köşeye A, kenarortayın kenarı kestiği noktaya D dersek;
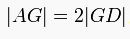 olur.
olur.Kenarortay teoremi
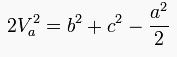
Üçgen İle İlgili Teoremler
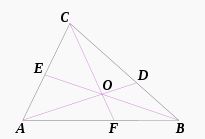
Seva Teoremi
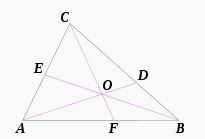
Seva Teoremi'nin uygulandığı üçgen
Seva teoremi, üçgenin köşelerinden karşıdaki kenarın herhangi bir noktasına çizilen doğrulardan oluşan şekilde uygulanan bir teoremdir. Uygulaması şu şekildedir:
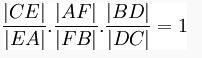
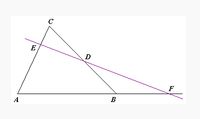
Menelaus Teoremi
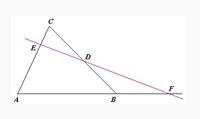
Menelaus Teoremi
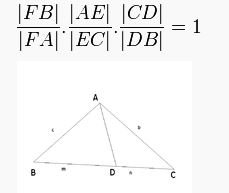
Üçgenle aynı düzlemde olan ve üçgenin köşelerinden geçmeyen herhangi bir doğrunun, üçgenin bir kenarının uzantısıyla kesişim noktalarının üçgenin köşelerine uzaklıkları arasındaki ilişkiyi anlatan teoremdir. Uygulaması:
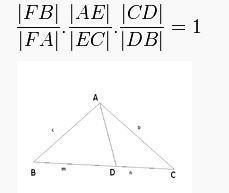
Steward Teoremi
Steward Teoremi, bir üçgende, bir köşeden karşı kenara çizilen herhangi bir doğru ile kenarlar arasındaki bir bağıntıdır. Bağıntı aşağıdaki gibidir:
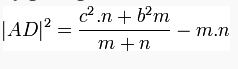
Carnot Teoremi
Carnot Teoremi
Üçgenin iç bölgesinde alınan herhangi bir noktadan kenarlara çizilen dikmelerle kenarlar sırasıyla a,b(ilk kenar) x,y(ikinci kenar) m,n(üçüncü kenar) olmak üzere parçalara ayrılsın.Benzerlik bağıntılarını kurduğumuzda:
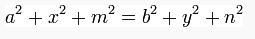
Son düzenleyen Safi; 2 Nisan 2016 07:58

 Üçgenlerin çevre ve alanı nasıl hesaplanır?
Üçgenlerin çevre ve alanı nasıl hesaplanır?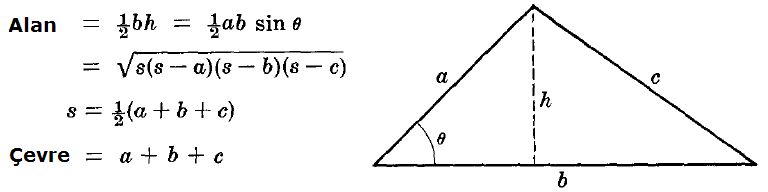
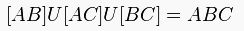
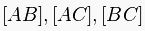 doğru parçaları üçgenin kenarlarıdır.
doğru parçaları üçgenin kenarlarıdır. 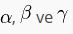 üçgenin iç açılarıdır.
üçgenin iç açılarıdır.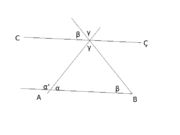
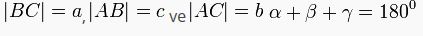

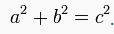
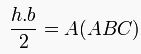 ayrıcaınızın başıyla da ölçebilirsiniz.
ayrıcaınızın başıyla da ölçebilirsiniz.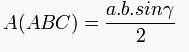
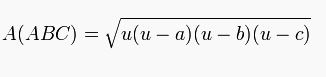
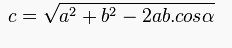

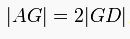 olur.
olur.