Ziyaretçi
Sayıların gelişim basamakları nelerdir?
Tarihte uzun zaman önce sayıları kendinde, kendi başına tasarlayamayan insan, henüz sayı saymayı bilmiyordu.Olsa olsa teki, çifti ve çoku tasarlayabiliyordu.Ruhbişlimcilerin ve budunbilimiclerin çalışmaları, kargadan başlayıp bebekten, Pigmeden ya da Fuegoludan geçip uygar insana giden gözlemlere dayanarak insanın sayı algısına ilişkin temel ilkenin ortaya konmasını sağlamıştır.
Hiçbir öğrenim görmemiş yetişkin bir insanın sayı algısı ancak 1den 4e kadardır.
Ameriakanın Asyanın ve Afrikanın dillerinde sayı adları olarak bir, iki ve çoktan başkası bulunmayan ama yinede birebir uygunluğu bilen kimi çağdaş insan
Ağaç kertme
Çakılları,çomakları üst üste yığma ya da yan yana dizme yolunu kullanıyorlar.
TARİHİN İLK RAKAMLARI
Bir gün birkaç saymanın aklına sıradan çakılların yerine uzlaşıma dayalı biçimler taşıyan,
Farklı boylarda
Pişmemiş topraktan yapılmış nesneleri koyma fikri geldi.
Nesnenin boyutu ve biçimi onu bir sayılama dizgesinin basamaklarından birinin karşılığı yapacaktı.
A. Milattan Önceki Devirlerde Sayılar
İlk çağlarda sayılar, kil tabletler üzerine çizikler, ağaç dallarına çentikler yapılarak ifade edilmiştir.
Eski Mısırda rakamlar, bazı şekillerin yan yana gelmesiyle belirtiliyordu: 1 için I, 10 için ^, 100 için ? (Çengel işareti) gibi. Eski Mezopotamyada ise 1 yerine D harfi, 10 Yerine 0 (yuvarlak) vb. şekiller kullanılıyordu. Eski Mısır ve Mezopotamyada sıfır rakamını gösteren sembole rastlanmamaktadır. Romalılarda harflerle gösterilen Romen Rakamlarını hepimiz biliyoruz: 1( 1 ), 5( V ), 10 ( X ), 50 ( L ), 100 ( C ). 500 ( D ), 1000 ( M ) gibi Romen rakamları da sıfır ve basamak sistemi ihtiva etmediğinden aritmetik işlemlere uygun değildir. Nitekim Romada, Forum meydanındaki süslü hitabet kürsüsünün Columna Restrata sütununda 2.200.000 sayısını belirtmek için, 22 adet yüz bini gösteren sayı işareti oyulmuştur. O devirde bu miktarı belirtmek için daha iyi bir işaret yoktu.
B. Hind Dünyasında Sayılar
Hindistan milattan 300 yıl önce sayı ifadelerini rakamlamaya başladı ve 6. Asra doğru haneleri sağdan sola doğru olan, 1 den 9a kadar rakamlar ortaya çıktı. Bu rakamlar 660 yıllarında Hindistan dışında da tanınmaya başlandı. Hintli Aryabhatta (476-550) Sanskrit dilinde bir matematik kitabı yazmış. p sayısı için 3.1416 değerini bulmuştur. Yine Brahmagupta (598-665) ve Bhaskara (doğ. 1114) matematikle ilgili kitaplar yazmışlardır.
C. İslâm Dünyasında Sayılar
Brahmagupta, astronomi ile ilgili yazdığı Siddhanta kitabında, ilk dokuz sayı işareti ve sıfır ile birlikte, hesap yapmaya dair kaideleri de almıştı. 773 yılında Kankah isimli bir Hintli astronom Halife El-Mansurun (754-775) Bağdattaki sarayına Brahmaguptanın bu kitabı ile gelir. Sindhind adıyla hemen Arapçaya çevrilen eser, halifeler tarafından astronomi araştırmaları için büyük himaye görür. Müslümanlar bu eserle Hint rakamlarını tanıdılar. Hint bilginleri daire şeklinde gösterdikleri 0 (sıfır) sayısına bir şeyin yokluğu anlamına gelen Sunya adını vermişlerdi; İslam bilginleri de bu işarete boşluk anlamına gelen es-sıfır demişlerdir.
İslâm âlimi El-Harezmi(780-850), zamanın Abbasi halifesi Memun(813-833)dan destek görür ve Bağdattaki saray kütüphanesindeki milattan önce ve sonra yazılan eski Mezopotamya, Mısır, Yunan, Hind (özellikle Sindhind) ve İslam alimlerinin kitaplarından (Kitab-ün-fil Hisab, Kitab-ün-fil-Coğrafya, vb.) yararlanarak kitaplar yazar. Bunların içinde en önemlisi girişte zikredilen El-Kitabül-Muhtasar fi Hesabil-Cebri vel-Mukabele kitabıdır. Bu eserin aslı İngiltere Oxford Bodlyn kütüphanesindedir. Bu eserde sıfır rakamı ve 9 ayrı rakamın aritmetik işlemlerde nasıl kullanılacağı açıkça gösterilmiş olup Kuran-ı Kerimdeki miras taksimi ve kölelerin serbest bırakılması mevzularıyla ilgili örnekler vardır. Bu eser İngiliz Bathlı Adelard tarafından Latinceye çevrilmiştir. Harezminin bu eseri Orta Çağda Latinceye çevrilirken, Adelard çevirisinde Arapça olan el-cebr kelimesini aynen almış ve bu kelime günümüze kadar algebra (=cebir) olarak aynen gelmiştir. Daha sonra 900lü yıllarda İspanyanın Kurtuba şehrindeki İslam halifesi II. Hakeme gönderilen Gerbert veya daha sonraki adıyla Papa II Silvester (945-1003) Batıda Arap Rakamlan olarak bilinen rakamlan (sıfır dahil) ilk defa Batıya öğretmiş ve ünü sekiz asır devam etmiştir. Gerbertden yüz yıl sonra Harezminin meşhur kitabının Latince tercümesi, Endülüs yoluyla Batıya ulaşır. Sonra Pizalı Leonardo Fibonacci (1170- ?) Mısıra yaptığı seyahatlerle matematik bilgisinin esaslarını orijinal kaynaklardan Batıya taşımıştır. Leonardo, İslam matematik öğretmenlerinden öğrendiği tüm bilgileri, sıfır rakamı dahil, çevresindekilere uygulamalarıyla öğretir ve Arapçada sıfır adı verilen . işareti ile her türlü hesabın yapılabileceğini açıklar.
Sayılar hakkında oldukça ilginç görüşlere sahip İhvan-ı Safaya göre, Kâinattaki âhenk sayılarla ortaya çıkarılır. Bu sayede çokluk birliğe dayanır. Dünya aritmetik ve geometrik ilişkilerle uyum içindedir ve Allahın birliğini gösteren bir şehri andırmaktadır.
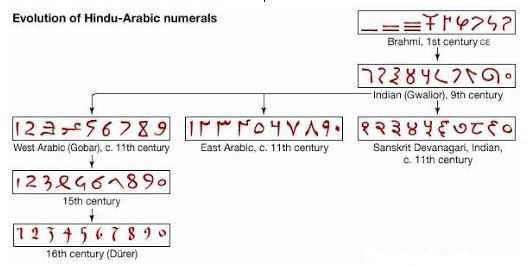
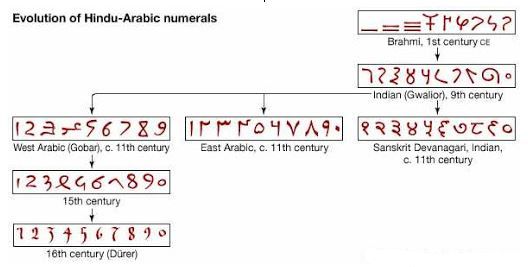
Milattan önceki devirler, Hint dünyası ve İslam dünyasında rakamların tarihi gelişimi aşağıdaki tabloda toplu olarak gösterilmektedir.
Sponsorlu Baglantilar
Ameriakanın Asyanın ve Afrikanın dillerinde sayı adları olarak bir, iki ve çoktan başkası bulunmayan ama yinede birebir uygunluğu bilen kimi çağdaş insan
Ağaç kertme
Çakılları,çomakları üst üste yığma ya da yan yana dizme yolunu kullanıyorlar.
TARİHİN İLK RAKAMLARI
Bir gün birkaç saymanın aklına sıradan çakılların yerine uzlaşıma dayalı biçimler taşıyan,
Farklı boylarda
Pişmemiş topraktan yapılmış nesneleri koyma fikri geldi.
Nesnenin boyutu ve biçimi onu bir sayılama dizgesinin basamaklarından birinin karşılığı yapacaktı.
- Birler basamağı için; Bir çubuk
- Onlar basamağı için; bir Bilya
- Yüzler basamağı için; Bir küre
- Küçük bir koni küçük bir kertikle
- Bir bilya küçük bir yuvarlak delikle
- Büyük bir koni kalın bir kertikle
- Bir küre bir daireyle betimlendi
A. Milattan Önceki Devirlerde Sayılar
İlk çağlarda sayılar, kil tabletler üzerine çizikler, ağaç dallarına çentikler yapılarak ifade edilmiştir.
Eski Mısırda rakamlar, bazı şekillerin yan yana gelmesiyle belirtiliyordu: 1 için I, 10 için ^, 100 için ? (Çengel işareti) gibi. Eski Mezopotamyada ise 1 yerine D harfi, 10 Yerine 0 (yuvarlak) vb. şekiller kullanılıyordu. Eski Mısır ve Mezopotamyada sıfır rakamını gösteren sembole rastlanmamaktadır. Romalılarda harflerle gösterilen Romen Rakamlarını hepimiz biliyoruz: 1( 1 ), 5( V ), 10 ( X ), 50 ( L ), 100 ( C ). 500 ( D ), 1000 ( M ) gibi Romen rakamları da sıfır ve basamak sistemi ihtiva etmediğinden aritmetik işlemlere uygun değildir. Nitekim Romada, Forum meydanındaki süslü hitabet kürsüsünün Columna Restrata sütununda 2.200.000 sayısını belirtmek için, 22 adet yüz bini gösteren sayı işareti oyulmuştur. O devirde bu miktarı belirtmek için daha iyi bir işaret yoktu.
B. Hind Dünyasında Sayılar
Hindistan milattan 300 yıl önce sayı ifadelerini rakamlamaya başladı ve 6. Asra doğru haneleri sağdan sola doğru olan, 1 den 9a kadar rakamlar ortaya çıktı. Bu rakamlar 660 yıllarında Hindistan dışında da tanınmaya başlandı. Hintli Aryabhatta (476-550) Sanskrit dilinde bir matematik kitabı yazmış. p sayısı için 3.1416 değerini bulmuştur. Yine Brahmagupta (598-665) ve Bhaskara (doğ. 1114) matematikle ilgili kitaplar yazmışlardır.
C. İslâm Dünyasında Sayılar
Brahmagupta, astronomi ile ilgili yazdığı Siddhanta kitabında, ilk dokuz sayı işareti ve sıfır ile birlikte, hesap yapmaya dair kaideleri de almıştı. 773 yılında Kankah isimli bir Hintli astronom Halife El-Mansurun (754-775) Bağdattaki sarayına Brahmaguptanın bu kitabı ile gelir. Sindhind adıyla hemen Arapçaya çevrilen eser, halifeler tarafından astronomi araştırmaları için büyük himaye görür. Müslümanlar bu eserle Hint rakamlarını tanıdılar. Hint bilginleri daire şeklinde gösterdikleri 0 (sıfır) sayısına bir şeyin yokluğu anlamına gelen Sunya adını vermişlerdi; İslam bilginleri de bu işarete boşluk anlamına gelen es-sıfır demişlerdir.
İslâm âlimi El-Harezmi(780-850), zamanın Abbasi halifesi Memun(813-833)dan destek görür ve Bağdattaki saray kütüphanesindeki milattan önce ve sonra yazılan eski Mezopotamya, Mısır, Yunan, Hind (özellikle Sindhind) ve İslam alimlerinin kitaplarından (Kitab-ün-fil Hisab, Kitab-ün-fil-Coğrafya, vb.) yararlanarak kitaplar yazar. Bunların içinde en önemlisi girişte zikredilen El-Kitabül-Muhtasar fi Hesabil-Cebri vel-Mukabele kitabıdır. Bu eserin aslı İngiltere Oxford Bodlyn kütüphanesindedir. Bu eserde sıfır rakamı ve 9 ayrı rakamın aritmetik işlemlerde nasıl kullanılacağı açıkça gösterilmiş olup Kuran-ı Kerimdeki miras taksimi ve kölelerin serbest bırakılması mevzularıyla ilgili örnekler vardır. Bu eser İngiliz Bathlı Adelard tarafından Latinceye çevrilmiştir. Harezminin bu eseri Orta Çağda Latinceye çevrilirken, Adelard çevirisinde Arapça olan el-cebr kelimesini aynen almış ve bu kelime günümüze kadar algebra (=cebir) olarak aynen gelmiştir. Daha sonra 900lü yıllarda İspanyanın Kurtuba şehrindeki İslam halifesi II. Hakeme gönderilen Gerbert veya daha sonraki adıyla Papa II Silvester (945-1003) Batıda Arap Rakamlan olarak bilinen rakamlan (sıfır dahil) ilk defa Batıya öğretmiş ve ünü sekiz asır devam etmiştir. Gerbertden yüz yıl sonra Harezminin meşhur kitabının Latince tercümesi, Endülüs yoluyla Batıya ulaşır. Sonra Pizalı Leonardo Fibonacci (1170- ?) Mısıra yaptığı seyahatlerle matematik bilgisinin esaslarını orijinal kaynaklardan Batıya taşımıştır. Leonardo, İslam matematik öğretmenlerinden öğrendiği tüm bilgileri, sıfır rakamı dahil, çevresindekilere uygulamalarıyla öğretir ve Arapçada sıfır adı verilen . işareti ile her türlü hesabın yapılabileceğini açıklar.
Sayılar hakkında oldukça ilginç görüşlere sahip İhvan-ı Safaya göre, Kâinattaki âhenk sayılarla ortaya çıkarılır. Bu sayede çokluk birliğe dayanır. Dünya aritmetik ve geometrik ilişkilerle uyum içindedir ve Allahın birliğini gösteren bir şehri andırmaktadır.
Milattan önceki devirler, Hint dünyası ve İslam dünyasında rakamların tarihi gelişimi aşağıdaki tabloda toplu olarak gösterilmektedir.

Son düzenleyen Safi; 2 Mayıs 2018 18:33

 Sayıların gelişim basamakları nelerdir?
Sayıların gelişim basamakları nelerdir?