Ziyaretçi
Arama
 Yedigenin iç açıları toplamı kaçtır?
Yedigenin iç açıları toplamı kaçtır?
En İyi Cevap Var Güncelleme: 7 Nisan 2020 Gösterim: 74.429 Cevap: 14
Ziyaretçi
6 Aralık 2010
Mesaj #1
Ziyaretçi
12 Ocak 2011
Mesaj #3
Ziyaretçi
Yedigen, yedi kenarı olan bir çokgendir. Yedigenin her köşesinden bir köşegen geçmez. Düzgün yedigenin tüm kenar uzunlukalrı ve açı ölçüleri birbirine eşit olmalıdır.Düzgün çokgenlerin bir dış açısı 360/kenar sayısı olduğundan, düzgün yedigenin bir dış açısı 360/7=51,428571... gibi tam sayı olmayan bir açıdır. Bu nedenle düzgün yedigeni çizmek çok zordur ve örneğine de pek rastlanmaz.
Ziyaretçi
21 Şubat 2011
Mesaj #4
Ziyaretçi
4 Mart 2011
Mesaj #5
Ziyaretçi
ÇOKGENLERİN İÇ AÇILARI TOPLAMI
Çizilen farklı çokgenler yardımı ile , çokgenlerin iç açıları toplamını belli bir kurala bağlama.
1 ) Öğrencilerden bilgisayarda açtıkları sayfaya herhangi bir beşgen, altıgen, yedigen, sekizgen çizmeleri istenir.
 a) Çizdikleri üçgenlerin herhangi bir köşesini tepe noktası, çokgenin kenarını taban kabul eden üçgenler çizmeleri istenir.
a) Çizdikleri üçgenlerin herhangi bir köşesini tepe noktası, çokgenin kenarını taban kabul eden üçgenler çizmeleri istenir. 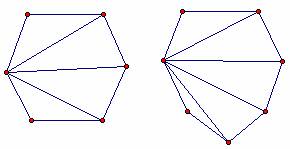
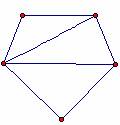
b) Öğrencilere çokgenlerden kaçar üçgen elde ettikleri ve burada bir şeyin dikkatlerini çekip çekmediği sorulur. Her türlü çokgen için kenar sayısının iki eksiği kadar üçgen oluştuğu cevabı gelince çocuklardan bu çokgenlerin içindeki üçgenlerin iç açıları toplamlarını bulmaları istenir.
x 180 = 540 4 x 180 = 720 5 x 180 = 900 6 x 180 = 1080
c) Çokgenlerin kenar sayısına n dersek, buldukları sonuçlardan yararlanarak bir genellemeye varılıp varılamayacağı sorulur. Sonuç olarak (n-2) x 180 cevabının gelmesi beklenir.
2 ) Öğrencilerden bilgisayarlarında yeni bir sayfa açmaları istenir. Yeni açtıkları sayfaya yine birer beşgen, altıgen, yedigen ve sekizgen çizmeleri istenir.
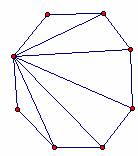
a) Çizdikleri çokgenlerin içinde bir nokta seçip, çokgenlerin kenarlarını taban kabul eden üçgenler çizmeleri istenir.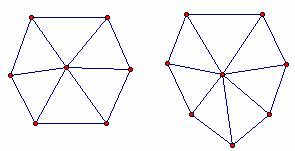
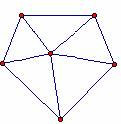
b) Çocuklara üçgenlerin iç açıları yardımı ile çokgenlerin iç açılarını bulup bulamayacakları sorulur. Cevap olarak üçgenlerin iç açıları toplamının çokgenlerin iç açıları toplamından 360 derece fazladır yanıtının gelmesi beklenir. Bunun nedeni sorulur.
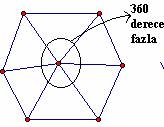 c) Bu sonuçlardan bir genellemeye varılıp varılamayacağı sorulur. n x 180 – 360 =( n – 2 ) x 180 Cevabı beklenir.
c) Bu sonuçlardan bir genellemeye varılıp varılamayacağı sorulur. n x 180 – 360 =( n – 2 ) x 180 Cevabı beklenir.
3 ) Her iki durumda da ulaşılan bağıntının aynı olduğu söylenir. n kenarlı dışbükey çokgenin iç açıları toplamı ( n – 2 ) x 180 teoremi ile bulunacağı ifade edilir. 4 ) Öğrencilerden dokuzgen ve onikigenin iç açıları toplamını bulmaları istenir. Dokuzgen için :
( 9 – 2 ) x 180 =1260
Onikigen için :
(12 – 2 ) x 180 =1800
Çizilen farklı çokgenler yardımı ile , çokgenlerin iç açıları toplamını belli bir kurala bağlama.
1 ) Öğrencilerden bilgisayarda açtıkları sayfaya herhangi bir beşgen, altıgen, yedigen, sekizgen çizmeleri istenir.






x 180 = 540 4 x 180 = 720 5 x 180 = 900 6 x 180 = 1080
c) Çokgenlerin kenar sayısına n dersek, buldukları sonuçlardan yararlanarak bir genellemeye varılıp varılamayacağı sorulur. Sonuç olarak (n-2) x 180 cevabının gelmesi beklenir.
2 ) Öğrencilerden bilgisayarlarında yeni bir sayfa açmaları istenir. Yeni açtıkları sayfaya yine birer beşgen, altıgen, yedigen ve sekizgen çizmeleri istenir.
a) Çizdikleri çokgenlerin içinde bir nokta seçip, çokgenlerin kenarlarını taban kabul eden üçgenler çizmeleri istenir.




3 ) Her iki durumda da ulaşılan bağıntının aynı olduğu söylenir. n kenarlı dışbükey çokgenin iç açıları toplamı ( n – 2 ) x 180 teoremi ile bulunacağı ifade edilir. 4 ) Öğrencilerden dokuzgen ve onikigenin iç açıları toplamını bulmaları istenir. Dokuzgen için :
( 9 – 2 ) x 180 =1260
Onikigen için :
(12 – 2 ) x 180 =1800
(n-2).180 Formülünde n yerine kenar sayısı konularak hesaplanır. (7-2).180 = 5.180 = 900 derecedir.
Ziyaretçi
6 Şubat 2012
Mesaj #7
Ziyaretçi
7 Şubat 2012
Mesaj #8
Ziyaretçi
İSMİ=yedigen Kenar Sayısı=7 İç Açıları Toplamı=900
İsmi=Sekizgen Kenar Sayısı=8 İç açıları Toplamı=1080
İsmi=Altıgen Kenar Sayısı=6 İç Açıları Toplamı=720
İsmi=Dokuzgen Kenar Sayısı=9 İç Açıları Toplamı=1260
İsmi=OnGen Kenar Sayısı=10 İç Açıları Toplamı=1440
İsmi=OnİkiGen Kenar Sayısı=12 İç Açıları Toplamı=1800
Hepsi Şuan Günümüzde Metamatikte Çokgenlerde Bulunan Kalıcı Bilimsel Değerlerdir.Formuluyle Hesaplarsanız Bile Çıkar.
Formül=
(n-2)x180 N=Kenar sayısıdır.
Mesale 7 geni hesaplayalım kenar sayısı 7.-2 Çıkarırsak 5 Kalıor.5i 180 İle Çarparsak Sonucu 900 Çıkar.Hepsi Formüllerle Kanıtlanmıştır.Birilerine Yardımcı Olabildiğsem Ne mutlu Bana.
7. sınıflar 2011/2012 Öğretim Yılı Metamatik Çalışma Kitabı Sayfa 65 5.Çalışma Da Bunlarla İlgili Bir Etkinlik Bulunmaktadır.Ben Zaten OnLARIN sonuçları Vermiş Oldum Bir Yönden.
Saygılarla.
İsmi=Sekizgen Kenar Sayısı=8 İç açıları Toplamı=1080
İsmi=Altıgen Kenar Sayısı=6 İç Açıları Toplamı=720
İsmi=Dokuzgen Kenar Sayısı=9 İç Açıları Toplamı=1260
İsmi=OnGen Kenar Sayısı=10 İç Açıları Toplamı=1440
İsmi=OnİkiGen Kenar Sayısı=12 İç Açıları Toplamı=1800
Hepsi Şuan Günümüzde Metamatikte Çokgenlerde Bulunan Kalıcı Bilimsel Değerlerdir.Formuluyle Hesaplarsanız Bile Çıkar.
Formül=
(n-2)x180 N=Kenar sayısıdır.
Mesale 7 geni hesaplayalım kenar sayısı 7.-2 Çıkarırsak 5 Kalıor.5i 180 İle Çarparsak Sonucu 900 Çıkar.Hepsi Formüllerle Kanıtlanmıştır.Birilerine Yardımcı Olabildiğsem Ne mutlu Bana.
7. sınıflar 2011/2012 Öğretim Yılı Metamatik Çalışma Kitabı Sayfa 65 5.Çalışma Da Bunlarla İlgili Bir Etkinlik Bulunmaktadır.Ben Zaten OnLARIN sonuçları Vermiş Oldum Bir Yönden.
Saygılarla.
Yedigen, yedi kenarı olan bir çokgendir. Yedigenin her köşesinden bir köşegen geçmez. Düzgün yedigenin tüm kenar uzunlukalrı ve açı ölçüleri birbirine eşit olmalıdır. Düzgün çokgenlerin bir dış açısı 360/kenar sayısı olduğundan, düzgün yedigenin bir dış açısı 360/7=51,428571... gibi tam sayı olmayan bir açıdır. Bu nedenle düzgün yedigeni çizmek çok zordur ve örneğine de pek rastlanmaz.
n kenarlı bir çokgenin iç açıları toplamı (n-2).180 bağıntısından bulunur.
Yedigenin kenar sayısı yani n=7 olduğundan (7-2).180=900
Birbirimize tutundukça ;Bıçakların ucu kapanacak.. ~





Benzer Konular
| 27 Aralık 2012 / Misafir Cevaplanmış |
| 2 Kasım 2012 / laz 61 Cevaplanmış |
| 25 Mart 2014 / Misafir Cevaplanmış |
| 9 Nisan 2015 / Misafir Cevaplanmış |
| 4 Ekim 2014 / Misafir Cevaplanmış |
| Kapat Saat: 19:55 Hoş Geldiniz Ziyaretçi
Benzer Konular
Son MesajlarYenile Yükleniyor... |


