Binom açılımı hakkında bilgi verir misiniz?
Ziyaretçi
Binom açılımı nedir, genel kuralları nelerdir?
Binom açılımı hakkında kısaca bilgi verip kurallarını anlatabilir misiniz?
Binom açılımı hakkında kısaca bilgi verip kurallarını anlatabilir misiniz?
Binom Açılımı
MsXLabs.org & Vikipedi, özgür ansiklopedi
Binom iki terimli demektir ve (x+y)n şeklinde bir iki terimlinin n. üssünü açtığımızda neler olduğu ile ilgilidir. Binom açılımına bildiğimiz iki binom açılımının özelliklerini inceleyerek başlayalım. Tam kare açılımı ve küp açılımı, çarpanlara ayırma konusundan bilmemiz gereken açılımlar:
(x+3y)8 açılımında 5. terim nedir ?
Çözüm
5. terim sorulduğundan ikinci değişkenin üssünün 4 olduğunu anlıyoruz. Dikkat edelim burada ikinci değişkeni katsayısı ile birlikte almalıyız.
(84)=70
Dolayısıyla terim
MsXLabs.org & Vikipedi, özgür ansiklopedi
Matematikte binom açılımı, iki sayının toplamının üslü ifadesinin açılımıdır.Temel Binom AçılımıSponsorlu Bağlantılar
n bir doğal sayı iken,Genelleştirilmiş Binom Açılımı
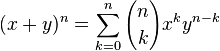
(sigma) Burada, n 'nin k 'li kombinasyonudur.
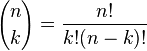
Kombinasyon tanımı gerçel ve karmaşık sayıları kapsayacak şekilde genelleştirildiği taktirde;
Temel Kurallar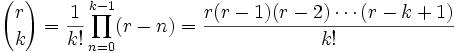
n'in bir doğal sayı olma şartı ortadan kalkar.
Binom iki terimli demektir ve (x+y)n şeklinde bir iki terimlinin n. üssünü açtığımızda neler olduğu ile ilgilidir. Binom açılımına bildiğimiz iki binom açılımının özelliklerini inceleyerek başlayalım. Tam kare açılımı ve küp açılımı, çarpanlara ayırma konusundan bilmemiz gereken açılımlar:
(x+y)2=x2+2xy+y2(x+y)3=x3+3x2y+3xy2+y3
İlk dikkat edeceğimiz özellik üs 2 iken binom açıldığında terim sayısı üç oldu. Üs 3'ken yani kübün açılımında da terim sayısı dört oldu. Beklenebileceği gibi üs n iken terim sayısı n+1'dir. Yani(x+y)n
açıldığında n+1 terim çıkar. İkinci önemli nokta, karenin açılımında bütün terimlerde değişkenlerin üsleri toplamı 2 ve kübün açılımında da 3'tür. Karenin açılımında ilk terim x2, ikinci terim 2xy=2x1y1 ve son terim de y2'dir ve üsler toplamı hep 2'dir. Küp açılımında ilk terim x3, ikinci terim katsayıyı önemsemezsek x2y, ve diğer iki terimde de üsler toplamı 3'tür. Hem karede hem de küpte, ilk ve son terimde bir tane değişken görünse de, ikinci değişken de ordaymış gibi düşünebiliriz. Örneğin karedeki ilk terimi x2 yerine x2y0 gibi küpteki son terim olan y3'ü de x0y3 gibi düşünebiliriz. Bunu, aşağıdaki iki sonucun her yerde geçerli olabilmesi için yapıyoruz: - (x+y)n açılımından (n+1) terim çıkar.
- Bütün terimlerde iki değişken de vardır ve üsleri toplamı n'dir. Birinci değişkenin üssü n'den başlar ve birer birer azalır, ikinci değişkenin üssü 0'dan başlar ve birer birer artar.
x3y0x2y1x1y2x0y3
Buraya kadar vurguladığımız sonuçlarla (x+y)6'nın açılımı için şunları yazabiliriz.(x+y)7=x7+x6y+x5y2+x4y3+x3y4+x2y5+xy6+y7
Önemli iki noktamız kaldı. Birincisi terimlerin başındaki katsayıların bulunuşu ve ikincisi de, bu uzun açılımı yapmadan istediğimiz bir terimi yazmanın yolları. Önce ikinci noktadan başlayalım. Örneğin yukarda 7. dereceden açılım yaptık. Bu açılımı yapmadan 5. terimi yazabilir miydik ? Bunun için y'nin üssünü kullanacağız, birinci terimde y'nin üssü 0, ikinci terimde 1, beşinci terimde 4, demek ki kaçıncı terimde isek y'nin üssü bu sayının 1 düşüğü. Örneğin (x+y)11 açılımında 7. terimi yazmaya çalışalım. 7. terim istendiği için y'nin üssü 6'dır. İki değişkenin üsleri toplamı her terimde 11 olmalıydı. Demek ki terim x5y6 şeklindedir. Geriye katsayıların nasıl bulunacağı kaldı. Katsayılar için kombinasyon formülü kullanacağız. Önce formülü hatırlayalım. n'nin r'li kombinasyonu(nr)=n!r!(n−r)!
(x+y)n açılımında a+b=n olmak üzere (üsler toplamı hep n) xayb şeklindeki bir terimin katsayısı (na) ya da (nb)'dir. Kaçıncı üssü açıyorsak onu kombinasyonda üste koyuyoruz ve değişkenlerden birinin üssünü de (istediğimizi seçebiliriz) alta koyuyoruz. Terim x5y6 şeklinde olduğundan, yukarıda (x+y)11 açılımında 7. terimin katsayısı,(116)=11!6!(11−6)!=11⋅10⋅9⋅8⋅75!=462
Örnek (x+3y)8 açılımında 5. terim nedir ?
Çözüm
5. terim sorulduğundan ikinci değişkenin üssünün 4 olduğunu anlıyoruz. Dikkat edelim burada ikinci değişkeni katsayısı ile birlikte almalıyız.
x?⋅(3y)4
8. üssü açtığımızdan üsler toplamı 8 olmalıdır dolayısıylax4⋅(3y)4
Kombinasyon formülünden katsayı (84)=70
70x4(3y)4=5670⋅x4⋅y4
Bu terimin katsayısı sadece kombinasyondan gelen 70 değildir. 34'te katsayıdır ve bu iki sayı çarpılınca katsayı 5670'tir. Son düzenleyen _Yağmur_; 26 Mart 2014 10:31
