Doppler Etkisi
Ziyaretçi
Doppler Etkisi
Doppler Etkisi (veya Doppler Olayı), adını ünlü bilim insani ve matematikçi Christian Andreas Doppler'dan almakta olup, kısaca dalga özelliği gösteren herhangi bir fiziksel varlığın frekans ve dalga boyu'nun hareketli (yakınlaşan veya uzaklaşan) bir gözlemci tarafından farklı zaman ve/veya konumlarda farklı algılanması olayıdır. Herhangi bir A konumundan B konumuna gitmek icin fiziksel bir dalga ortamı'na ihtiyaç duyan dalgalar (orn. ses dalgalari veya su dalgalari) icin Doppler Etkisi hesaplamaları yapılırken, dalga kaynağı ve gözlemcinin birbirine gore konum, yön ve hızlarının yanında dalganın içinde veya üzerinde hareket ettiği dalga ortamının da fiziksel yapısı (yoğunluk, hacim, iletkenlik katsayısı, kimyasal özellikleri, vb.) dikkate alınmak zorundadır. Eğer söz konusu dalga herhangi bir A konumundan B konumuna gitmek için fiziksel bir dalga ortamına ihtiyaç duymuyor ise (orn. ışık, radyo dalgaları veya radyasyon) Doppler Etkisi hesaplamalarında sadece dalga kaynağının ve gözlemcinin birbirine göre birim zamandaki konumlarının değerlendirilmesi yeterlidir.
Tarihçe
Doppler Etkisi ilk olarak 1842 yilinda Avusturya'li bilim insani Christian Andreas Doppler tarafindan (Über das farbige Licht der Doppelsterne und einige andere Gestirne des Himmels soylemi ile) matematiksel bir hipotez olarak ortaya atilmistir. 1845 yilinda Hollanda'li fizikci Christophorus Ballot tarafindan ses dalgalari kullanilarak test edilmis ve "ses kaynagi kendisine yakinlasirken duydugu frekansin yukseldigini, uzaklasirken ise dustugunu ispatladigini" soylemesi ile resmen onaylanmistir. Ayni etki Ballot veya Doppler'dan bagimsiz olarak 1848 yilinda Fransiz fizikci Hippolyte Fizeau tarafindan elektromanyetik dalgalar uzerinde de kesfedilmistir. Bu yuzden nadiren de olsa bazi bilim cevrelerince Doppler-Fizeau Etkisi olarak da bilinir.
Matematiksel Analiz
Doppler Etkisi konusunda bilinmesi gereken en onemli husus, her ne kadar gozlemci dalga frekansinin kendi hareketi ya da dalga kaynaginin hareketi huzunden degistigini gorse de, aslinda frekansin sabit kaldigi gercegidir. Tam olarak ne oldugunu daha iyi anlamak icin soyle bir ornek uzerinde dusunelim: Siz yerinizde ve hareketsizsiniz. Bir arkadasiniz sizden 10 metre uzakta duruyor ve size her saniyede bir elindeki tenis toplarindan birini firlatiyor. Burada arkadasinizin toplari her seferinde ayni dogru boyunca ve ayni hizda attigini varsayalim. Eger arkadasiniz da hareketsiz ise her saniyede bir 10 metre yol kateden tenis toplarindan biri size ulasacaktir. Simdi arkadasinizin yine her sahinyede bir top firlattigini (yani aslinda top firlatma frekansi degismiyor), ancak bu sefer size dogru yurumeye basladigini ongorelim. Bu durumda size ulasan iki top arasindaki sure 1 saniyeden daha kisa olacaktir cunku toplar her seferinde 10 metre, 9 metre, 8 metre seklinde daha az mesafe katettikten sonra size ulasacaktir. Elbette ayni etkinin zitti arkadasiniz sizden uzaklasirken de gecerli olacaktir. Bir baska degisle, toplar arkadasinizin elinden her zaman saniyede bir ciktigi halde, sizin ya da arkadasinizin hareketi yuzunden size azalan ya da artan zamanlarda ulasacaktir. Bu da dogal olarak arkadasinizin size topu farkli zamanlarda firlattigini dusunmenize sebep olur. Yani aslinda Doppler Etkisi'nde "etkilenen" asil fiziksel degisken dalga boyu'dur. Elbette dalga boyu ile frekans ters orantili oldugundan gozlemciye gore dalga kaynaginin frekansi da degisiyor gibi gorunur.
Eger (f0) frekansinda dalga yayan hareketli bir kaynak bu yayilimi sadece kendinin ve bir gozlemcinin bulundugu sabit bir dalga ortaminda yapiyorsa, o zaman bu dolga ortamina gore hareketsiz olan bir gozlencinin gorecegi frekansi (f) bulmak icin:
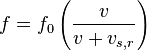
formulu kullanilir. Burada (v) dalga ortamindaki dalgalarin hizi, (vs, r) ise kaynagin sabit olan dalga ortamina gore (eger gozlemciye dogru hareket ediyorsa (+) arti bir deger, ters yonde hareket ediyorsa (-) eksi bir deger) hizidir. Benzer bir analiz sabit bir dalga kaynagi ile hareketli bir gozlemci icin asagidaki gibidir. (vo) = Gozlemcinin dalga ortamina gore hizi.
Yukaridaki ornekte de gordugumuze benzer sekilde, bu sefer gozlemcinin dalga kaynagindan uzaklasmasi durumunda (vo) degeri (+) arti, yakinlasmasi durumunda ise (-) eksi olur.
Matematiksel olarak bu iki formul elbette tek bir vektorel esitlik olarak genellestirilebilir. Koordinat sisteminin dalga ortami uzerindeki herhangi bir noktanin konumunu verdigini, ve bu ortamda ses hizi'nin (c) oldugunu varsayalim ve soz konusu ortamda (s) kaynaginin (
) hiziyla hareket edip cevresine (fs) frekansinda dalgalar yaydigini ongorelim. Bu dalga ortaminda birde (
) hiziyla hareket eden bir (r) gozlemcisi olsun. Dalga kaynagi (s) ile gozlemci (r) arasindaki matematik vektorun ise (
) oldugunu ongorelim. (Yani 
)
Bu durumda gozlemcinin algilayacagi frekans (fr):
esitliginden bulunabilir. Eger
ise, o zaman algilanan frekanstaki degisim daha cok dalga kaynagi ve gozlemcinin birbirine gore hizlarina bagli olur:
Veya alternatif olarak:
Doppler'in bu analizinin isik isinlari icin de gecekli olabilmesi icin yapilan ilk calisma Hippolyte Fizeau tarafindan yurutulmustur. Ancak isik A noktasindan B noktasina gidebilmek icin belli bir dalga ortamina gerek duymaz (ornegin sonsuz bosluk olan uzayda kolayca yol alir) ve Doppler Etkisi'nin isik isinlarina nasil dogru bir sekilde uygulanabileceginin anlasilabilmesi icin Einstein'in Ozel Gorelilik (izafiyet) teorisinin kullanimina ihtiyac vardir.
Sponsorlu Bağlantılar
Tarihçe
Doppler Etkisi ilk olarak 1842 yilinda Avusturya'li bilim insani Christian Andreas Doppler tarafindan (Über das farbige Licht der Doppelsterne und einige andere Gestirne des Himmels soylemi ile) matematiksel bir hipotez olarak ortaya atilmistir. 1845 yilinda Hollanda'li fizikci Christophorus Ballot tarafindan ses dalgalari kullanilarak test edilmis ve "ses kaynagi kendisine yakinlasirken duydugu frekansin yukseldigini, uzaklasirken ise dustugunu ispatladigini" soylemesi ile resmen onaylanmistir. Ayni etki Ballot veya Doppler'dan bagimsiz olarak 1848 yilinda Fransiz fizikci Hippolyte Fizeau tarafindan elektromanyetik dalgalar uzerinde de kesfedilmistir. Bu yuzden nadiren de olsa bazi bilim cevrelerince Doppler-Fizeau Etkisi olarak da bilinir.
Matematiksel Analiz
Doppler Etkisi konusunda bilinmesi gereken en onemli husus, her ne kadar gozlemci dalga frekansinin kendi hareketi ya da dalga kaynaginin hareketi huzunden degistigini gorse de, aslinda frekansin sabit kaldigi gercegidir. Tam olarak ne oldugunu daha iyi anlamak icin soyle bir ornek uzerinde dusunelim: Siz yerinizde ve hareketsizsiniz. Bir arkadasiniz sizden 10 metre uzakta duruyor ve size her saniyede bir elindeki tenis toplarindan birini firlatiyor. Burada arkadasinizin toplari her seferinde ayni dogru boyunca ve ayni hizda attigini varsayalim. Eger arkadasiniz da hareketsiz ise her saniyede bir 10 metre yol kateden tenis toplarindan biri size ulasacaktir. Simdi arkadasinizin yine her sahinyede bir top firlattigini (yani aslinda top firlatma frekansi degismiyor), ancak bu sefer size dogru yurumeye basladigini ongorelim. Bu durumda size ulasan iki top arasindaki sure 1 saniyeden daha kisa olacaktir cunku toplar her seferinde 10 metre, 9 metre, 8 metre seklinde daha az mesafe katettikten sonra size ulasacaktir. Elbette ayni etkinin zitti arkadasiniz sizden uzaklasirken de gecerli olacaktir. Bir baska degisle, toplar arkadasinizin elinden her zaman saniyede bir ciktigi halde, sizin ya da arkadasinizin hareketi yuzunden size azalan ya da artan zamanlarda ulasacaktir. Bu da dogal olarak arkadasinizin size topu farkli zamanlarda firlattigini dusunmenize sebep olur. Yani aslinda Doppler Etkisi'nde "etkilenen" asil fiziksel degisken dalga boyu'dur. Elbette dalga boyu ile frekans ters orantili oldugundan gozlemciye gore dalga kaynaginin frekansi da degisiyor gibi gorunur.
Eger (f0) frekansinda dalga yayan hareketli bir kaynak bu yayilimi sadece kendinin ve bir gozlemcinin bulundugu sabit bir dalga ortaminda yapiyorsa, o zaman bu dolga ortamina gore hareketsiz olan bir gozlencinin gorecegi frekansi (f) bulmak icin:
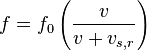
formulu kullanilir. Burada (v) dalga ortamindaki dalgalarin hizi, (vs, r) ise kaynagin sabit olan dalga ortamina gore (eger gozlemciye dogru hareket ediyorsa (+) arti bir deger, ters yonde hareket ediyorsa (-) eksi bir deger) hizidir. Benzer bir analiz sabit bir dalga kaynagi ile hareketli bir gozlemci icin asagidaki gibidir. (vo) = Gozlemcinin dalga ortamina gore hizi.
Yukaridaki ornekte de gordugumuze benzer sekilde, bu sefer gozlemcinin dalga kaynagindan uzaklasmasi durumunda (vo) degeri (+) arti, yakinlasmasi durumunda ise (-) eksi olur.
Matematiksel olarak bu iki formul elbette tek bir vektorel esitlik olarak genellestirilebilir. Koordinat sisteminin dalga ortami uzerindeki herhangi bir noktanin konumunu verdigini, ve bu ortamda ses hizi'nin (c) oldugunu varsayalim ve soz konusu ortamda (s) kaynaginin (
) hiziyla hareket edip cevresine (fs) frekansinda dalgalar yaydigini ongorelim. Bu dalga ortaminda birde () hiziyla hareket eden bir (r) gozlemcisi olsun. Dalga kaynagi (s) ile gozlemci (r) arasindaki matematik vektorun ise () oldugunu ongorelim. (Yani )Bu durumda gozlemcinin algilayacagi frekans (fr):
esitliginden bulunabilir. Eger
ise, o zaman algilanan frekanstaki degisim daha cok dalga kaynagi ve gozlemcinin birbirine gore hizlarina bagli olur: Veya alternatif olarak:
Doppler'in bu analizinin isik isinlari icin de gecekli olabilmesi icin yapilan ilk calisma Hippolyte Fizeau tarafindan yurutulmustur. Ancak isik A noktasindan B noktasina gidebilmek icin belli bir dalga ortamina gerek duymaz (ornegin sonsuz bosluk olan uzayda kolayca yol alir) ve Doppler Etkisi'nin isik isinlarina nasil dogru bir sekilde uygulanabileceginin anlasilabilmesi icin Einstein'in Ozel Gorelilik (izafiyet) teorisinin kullanimina ihtiyac vardir.
