".. Bilimciler, şüphe ve kesinsizlikle iş görmeye alışıktırlar. Tüm bilimsel bilgi kesinsizdir. Şüphe ve kesinsizlikle ilgili bu deneyim önemlidir. Ben bu deneyimin çok büyük bir değer taşıdığına ve bilimin ötesinde de genişletilmesi gerektiğine inanıyorum. İnanıyorum ki, daha önce çözülememiş herhangi bir problemi çözmek için, kapıyı bilinmeyene aralık bırakmak zorundasınız. Tam olarak doğru biçimde kestiremediğiniz olasılığa fırsat vermek zorundasınız. Aksi takdirde, eğer zihniniz önceden hazırlarsanız, problemi çözemeyebilirsiniz." R.Feynman
Belirsizlik İlkesi.
Belirsizlik İlkesi nedir? İnsanoğlu olarak bizler her şeyi bilebilir miyiz? Yoksa bilme yetimiz sınırlı mı? Kuantum kuramının Kopenhag Yorumu, "öznel idealist" bir yorum mudur? Elektron aynı anda iki delikten geçer mi?
Otomobille yola çıkan ve bize yola çıkış saatini bildiren insanların yaklaşık da olsa saat kaçta nerede olacaklarını tahmin ederiz. Bu tahminimiz, arabayı kullananın trafik canavarı ruhuna sahip değilse çoğunlukla doğru çıkar. Bir uyduyu Dünya çevresine yerleştirmek istesek, istediğimiz uzaklıktaki bir yörüngeye yerleştirebiliriz. Klasik fizik yasaları, bize kesin öngörme olanakları verir. Örneğin bir roketin ateşlendikten sonra izleyeceği rotayı, bir süre sonra varacağı noktayı kesin olarak hesaplayabiliriz. Roketin hızını ve rotasını etkiyebilecek değişkenleri daha duyarlı ölçersek hesaplarımız daha doğru olur. Gerçekte erişebileceğimiz doğruluğun sınırı yoktur. Klasik fizikte hiçbir şey şansa bırakılmaz, fiziksel davranışlar önceden tahmin edilebilir. Oysa modern fizikte fiziksel davranışlar, olasılıklar açısından öngörülebilir.
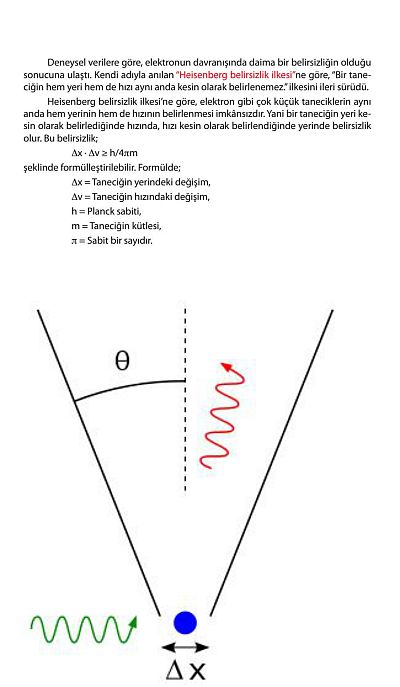
1920'lerde Niels Bohr ve Werner Heisenberg, atomlardan daha küçük (atomaltı) taneciklerin davranışlarının ne dereceye kadar belirlenebileceğini görebilmek için düşünsel (hipotetik) deneyler tasarladılar. Bunun için taneciğin konumu ve momentumu gibi iki değişkenin ölçülmesi gerekliydi. Tanecik ya da parçacık şu anda nerededir? Kütle ve hız çarpımı nedir? Onların eriştiği sonuca göre ölçümde daima bir belirsizlik olmalıydı ve bu belirsizliklerin çarpımı Planck sabitinin 4 pi'ye bölümüne eşit veya ondan daha büyük bir sabit oluyordu. Heisenberg belirsizlik ilkesi diye anılan bu ilkeye göre: bir taneciğini konumu ve ve momentumu aynı anda tam bir duyarlılıkla ölçülemez. Örneğin bir taneciğin konumunu kesin şekilde belirleyecek bir deney tasarlasak, onun momentumunu duyarlı şekilde ölçemeyiz; momentum belirlenebiliyorsa bu kez de taneciğin konumunu belirleyemeyiz. Basit bir deyişle, eğer bir taneciğin nerede olduğunu kesin olarak biliyorsak, aynı anda taneciğini nereden geldiğini veya nereye gittiğini kesin şekilde bilemeyiz. Benzer şekilde bir taneciğini nasıl hareket ettiğini biliyorsak onun nerede olduğunu belirleyemeyiz. Bir parçacığın momentumunun ya da konumunun ayrı ayrı belirlenmesinde bir sınır yoktur. Ancak momentum ve konum aynı anda yani aynı dalga fonksiyonu için belirlenmesinde temel bir sınır vardır. Atomaltı dünyada nesneler, daima belirsizliklere neden olmalıydı. Neden böyle olması gerekiyordu?
Elektronu "Görmek"
Hidrojen atomundaki elektronu "görmek" ve hareketlerini "izlemek" istiyoruz. Bir mikroskop kullanmak zorundayız. Mikroskopta görmek istediğiniz en küçük taneciği görebilmek için tanecik boyutu ile ışığın boyutu aynı olmak zorunda. Görünür ışıktan yararlandığımız normal bir mikroskopta görülebilecek en küçük boyut yaklaşık 1000 nm dir. Bir elektron mikroskobunun çözümleme gücü ise yaklaşık 1 nm dir. Elektronu görünür ışıkla göremeyiz . Çünkü görünür ışığı, hidrojen atomuna gönderdiğimizde elektron, atomdan kopup gider; yani görünür ışık hidrojen atomunu iyonlaştırır. Yapabileceğimiz tek şey var: Dalga boyu daha küçük ışık seçmek. Durum yine değişmiyor. Çünkü elektrona çarpan fotonlar, elektronunun atom içindeki "konumunu" ve "hızı"nı değiştiriyor. Ve biz elektronu asla atomdaki gerçek konumunda göremiyoruz. Ayrıca elektrona çarpan foton, elektronun hızını ve buna bağlı olarak momentumunu (kütle ile hızın çarpımını) değiştirir. Biz bu değişmiş olan nicelikle karşılaşırız.
"Heisenberg' in belirsizlik ilkesi, bir sitemin durumunun tam olarak ölçülemeyeceğini, bu yüzden onun gelecekte tam olarak ne yapacağı konusunda kestirimde bulunulamayacağını göstermiştir. Tüm yapılabilecek şey, farklı sonuçların olasılıkları hakkında kestirimde bulunmaktır. Einsten' i o kadar huzursuz eden şey, işte bu şans ya da rasgelelik unsuru idi. Albert Einstein, fiziksel yasaların, gelecekte ne olacağına ilişkin belirli, muğlak (belirsiz) olamayan bir kestirimde bulunulmasına inanmayı reddetti. Fakat, nasıl ifade edilirse edilsin, kuantum olayı ve belirsizlik ilkesinin kaçınılmaz oldukları ve fiziğin her dalında onlarla karşılaşıldığı konusunda her tür kanıt vardır."
Foto elektrik olayın tam sonuçları, 1925 de Werner Heisenberg' in açıklamasıyla anlaşıldı.
Foto elektrik olay, bir parçacığın konumunu tam olarak ölçme olanağı tanıyordu.
Bir parçacığın ne olduğunu anlamak için onu ışığa tutmalısınız. Peki ışık, sonsuz olarak bölünebilir mi? Bu sorunun yaklaşık yüz yıl önce maddeler için sorulduğunu anımsayınız. İlk bakışta ışık niye sonsuz dilimlere ayrılmasın serzenişiyle yanıtlanır. Einstein, ışığı sonsuz küçük miktarda kullanamayacağımızı göstermiştir. En azından bir paket yani bir kuantum kullanabiliriz. Bu ışık paketi, parçacığı etkiler ve onun herhangi bir yönde bir hızla hareket etmesine yol açar. Parçacığın konumunu ne kadar duyarlı (hassas) ölçmek isterseniz, kullanmak zorunda kalacağınız paketin enerjisi o kadar büyük olur , ama ışık bu durumda parçacığı daha fazla etkiler. Ancak siz parçacığın konumunu nasıl ölçmeye çalışırsanız çalışın, konumdaki belirsizlik ile hızındaki belirsizliğin çarpımı, her zaman belirli bir minimum miktardan büyük olur. Ünlü Belirsizlik ilkesini dinlediniz, hem de Stephen Hawking' den.
(S.Hawking, Karadelikler Ve Bebek Evrenler, s:81)
Belirsizlik ilkesinin kabul edilmesi çoğumuz için kolay değildir. Einstein bile 1920' lerin ortasından 1955' te ölümüne dek bu kuramı çürütmek amacı ile yaptığı başarısız girişimlerle zamanının önemli bir kısmını harcamıştır.
Genel görelilik kuramı, artık klasik bir kuramdır; çünkü belirsizlik ilkesini kapsamıyor. Einstein de, bir klasik fizikçidir; çünkü kuantum olaylarındaki raslantıyı ve bilinemezliği kabul etmiyor.
Belirsizlik İlkesine Felsefi Saldırı
Belirsizlik İlkesi,kimi felsefeciler tarafından hala anlaşılmış görünmüyor. Onlar,doğrudan belirsizlik ilkesine karşı çıkmadan Kuantum kuramının Kopenhag Yorumuna saldırıyorlar,Heisenberg'e saldırıyorlar. Kopenhag Yorumunu, "öznel idealist" likle itham ediyorlar. Bu arada büyük Einstein'ı yanlarına almaya çalışıyorlar! Ama büyük Einstein onları şaşırtıyor. Çünkü onlar özel göreliliği ve genel göreliliği de güvenilir görmüyorlar. Dolaysıyla elde saldırılmadık kuram kalmıyor. Bu insanlar,bilimde kesinsizliği,bilimde belirsizliği kabullenemiyorlar. Doğanın böyle olmadığını kuramın eksik ve belirsiz olduğunu iddia etmeye devam ediyorlar. "Devam ediyorlar" diyorum,çünkü kurama yöneltilen bu eleştiriler 70 yıldır sürüyor. Oysa kuantum kuramı ve de bunun Kopenhag Yorumu,bu zaman diliminde gözlemlerle uyuşmaya devam ediyor. Elbette ölümsüz kuram yoktur,zaman eleğin daha dar gözeneklerini bilimin önüne dikecektir;ama bunun belirsizlik ilkesini aşamayacağı büyük bir olasılık gibi görünüyor.
Bilimin ya da bildiğinin "kesinliğini" iddia edenler, tarihte görüldüğü gibi çok tehlikeli düşüncelerdir. Böyle düşünen insanlar, değişime açık değildir;yeni şeyler öğrenmeye açık değildir. Kimi insanların akşam sabah "bir ırmakta iki kere yıkanılmaz"(Herakleitos) demesi,onun tutucu olmadığının bir kanıtı değildir. Bu insanların bilim anlayışı 19.yy mekanizmine takılıp kalmıştır.
Bir başka nokta,belirsizlik ilkesinin "insan onurunu" çiğnediği,insanın bilme olanaklarına sınır getirdiği düşüncesidir. Buna göre belirsizlik ilkesi,insanı neredeyse evrenin çok önemsiz bir varlığı haline getirmektedir. Oysa belirsizlik ilkesi,insanoğlunun yetersizliğine,güçsüzlüğüne yorulan bir gerçek değildir. Tam da tersine,belirsizlik ilkesinin keşfi, doğanın önümüze koyduğu ince bir uyarı levhasının görülmesidir. İnsanın neyi ne kadar bilebileceğini bilmesidir.Bu konuda Richart Feynman ' ın bir konuşmasını aşağıda veriyorum:
"Yasalar Nasıl Keşfedilir? "
"Orta Çağlar' da insanların basitçe çok sayıda gözlem yaptığı ve bu gözlemlerin de yasaları akla getirdiği düşünülüyordu. Fakat gerçek bu değildir. O, gözlemden daha çok imajinasyon(hayal gücü) gerektirmektedir. Bu nedenle, öncelikle konuşmamız gereken şey, yeni düşüncelerin nereden geldiğidir. Gerçekte fikirlerin geldiği sürece, nereden gelmiş olduklarının önemi yoktur. Bizim bir fikrin doğru olup olmadığını kontrol etmemizin, onun nereden geldiğiyle hiçbir ilgisi olmayan bir yolu vardır. Biz basit biçimde onu gözlemle test ediyoruz. Bu nedenle bilimde bir fikrin nereden geldiğiyle ilgilenmiyoruz.
İyi bir düşüncenin hangisi olduğuna karar veren bir otorite yoktur. Bir düşüncenin hangisi doğru olup olmadığını bulmak için bir otoriteye gitmeye ihtiyacımız kalmadı. Biz bir otoriteyi okuyabilir ve bir önerisini ele alabiliriz; sonra da onu deneyebilir ve doğru olup olmadığını bulabiliriz. Eğer doğru değilse, "otoriteler" "otoritelerinden" kaybederler.
Bilim adamları arasındaki ilişkiler başlangıçta, çoğu insanların arasında olduğu gibi ihtilaflıydı. Örneğin, fiziğin erken günlerinde bu böyleydi. fakat günümüz fizikçileri arasındaki ilişkiler son derece iyidir. Bir bilimsel argümanı tartışan taraflar arasında gülünecek birçok şey olabilir ve her iki tarafta henüz belirsizlikler bulunabilir. Taraflar yeni deneyler düşünebilir ve sonuç hakkında bahse tutuşma önerileri getirebilirler. Fizikte o kadar çok sayıda birikmiş gözlem vardır ki, daha önce yapılmış gözlemlerle uyum içinde ama daha önce düşünülmüş tüm fikirlerden farklı olan yeni bir şey ortaya atmak neredeyse imkansız hale gelmiştir.
Bu nedenle eğer birinden veya bir yerden yeni bir şey işitirseniz onu hoş karşılarsınız ve diğer kişinin niçin böyle konuştuğu hakkında tartışmazsınız.
Birçok bilim dalı bu ölçüde gelişme göstermedi ve bu dallardaki durum fiziğin erken günlerindeki gibidir. Yani çok sayıda gözlem olmadığı için birçok tartışma yapılmaktadır. Bundan söz etmemin nedeni insan ilişkilerinin ilginç özelliğidir; eğer gerçeği belirlemenin bağımsız bir yolu bulunursa ihtilaflar sona erebilir.
Çoğu insan, bilimde bir düşüncenin sahibinin arka planına ya da onun bu fikirleri açıklamasına yol açan güdülere ilgi gösterilmemesini şaşırtıcı bulmaktadır. Dinlersiniz, eğer denemeye değer bir şey, denenebilir bir şey gibi geliyorsa size, o farklı demektir. Ve eğer daha önce gözlenmiş bir şeyle açık olarak çelişmiyorsa, heyecan vericidir ve harcanan zahmetlere değer. Onun ne kadar süreyle bu konuyu incelediğinin ya da niçin sizin kendisini dinlemenizi istediğinin önemi yoktur. Bu anlamda fikrin geldiği yer de herhangi bir farklılık yaratmaz. gerçek kaynak bilinmeden kalır; biz bunu, insan beyninin imajinasyonu, yaratıcı imajinasyonu (muhayyile) olarak adlandırıyoruz. Bilinen, onun sadece bir tür enerji olduğudur.
İnsanların bilimde imajinasyon olduğuna inanmaması şaşırtıcıdır. Bilimdeki imajinasyon, sanattakinden farklı olan çok ilginç bir imajinasyon türüdür. İmajinasyon yapmaya çalışmadaki büyük zorluk şunlardan kaynaklanır; daha önce hiç görmediğiniz bir şey olacak, daha önce görülmüş, ele alınmış her detayı kapsayacak, o ana kadar düşünülmüş olandan farklı olacak ve daha da ötede; kesin olacak ve herhangi bir muğlaklık içermeyecek. Bu, gerçekten zor bir şeydir.
Öte yandan, kontrol edilebilecek kuralların varlığı, bir tür mucizedir. Gravitasyonun ters kare yasası gibi bir kuralı bulmak mümkündür fakat mucize kabilinden bir şeydir. Bu tamamen anlaşılmaz bir şeydir, fakat size öngörüde bulunabilme olanağı sağlar. Bunun anlamı onun, henüz yapmadığınız bir deneyde neyin olmasını bekleyeceğinizi size söylüyor olmasıdır.
Ayrıca mutlak bir temel olarak, bilimin çeşitli kuralları karşılıklı olarak uyumlu olmalıdır. Gözlemler tamamen aynı gözlemler olduğu sürece, bir kuralı, bir öngörüyü, başka bir kuralın da başka bir öngörüyü vermesi mümkün değildir. Bu nedenle bilim, özel bir iş değildir, tamamen evrenseldir. Ben fizyolojideki atomlar hakkında konuştum; astronomi, elektrik ve kimyadaki atomlar hakkında konuştum. Bunlar evrenseldir; karşılıklı olarak uyumlu olmalıdırlar. Atomlardan oluşmayan yeni bir şeyle ortaya çıkamazsınız.
İlginçtir ki, akıl, tahminleri kurallara sokar ve kurallar en azından fizikte azalmıştır. Kimyada ve elektrikteki kuralları tek bir kurala indirgemenin güzel bir örneğini vermiştim.
Doğayı betimleyen kurallar, matematiksel kurallar olarak görünmektedir. Bu özellik, gözlemin bir yargıç hüviyetinde olmasından kaynaklanmamaktadır. Ayrıca, matematiksel olmak, bilimin zorunlu bir karakteristiği de değildir. O sadece sizin en azından fizikte güçlü öngörüler yapmaya yarayan matematiksel yasaları ifade edebilmenize imkan verir. tekrar konuya dönersek, doğa niçin matematikseldir? Bu, bir sırdır.
Şimdi önemli bir noktaya geliyorum. Eski yasalar yanlış olabilir. Bir gözlem nasıl yanlış olabilir? Niçin fizikçiler yasaları sürekli değiştiriyorlar? Yanıt öncelikle şudur ki, yasalar gözlemler değildir. İkincisi, deneyler her zaman doğru değildir. Yasalar tahmin edilmişlerdir, ekstrapole edilmişlerdir. Onlar sadece şimdiye kadar süzgeçten geçmiş olan iyi tahminlerdir. Ancak şimdiki süzgeçlerin delikleri, daha önce kullanılan süzgeçlerin deliklerinden daha küçüktür. Bu nedenle yasa şimdi süzgeçte kalarak yakalanabilir. Yasalar, tahminlerdir ve bilinmeyene extrapole edilmişlerdir. Ne olacağını bilmiyorsanız, bir tahminde bulunursunuz.
Örneğin bir şeyin hareketinin onun ağırlığını etkilemeyeceğine inanılıyordu - bu keşfedilmişti - . Eğer bir topacı döndürür ve tartarsanız ve sonra onu durdurduğunuzda tartarsanız, aynı ağırlıkta olduğunu görürsünüz. Bu bir gözlemin sonucudur. fakat bir şeyi, ondalık basamakların çok küçük bölümlerinde, milyarda bir bölümlerinde tartamazsınız. Biz şimdi biliyoruz ki, dönmekte olan bir topaç, durmakta olan bir topaçtan milyarlardan küçük birkaç bölüm kadar daha ağır gelmektedir. Eğer topaç, saniyede 186.000 mile yakın bir hızda döndürebilirse, ancak o zaman topacın ağırlığındaki artış farkedilebilir duruma gelebilecektir. İlk deneylerde topaç saniyede 186.000 milden aşağıdaki hızlarla çevrilmişti. O durumda dönen topacın kütlesiyle dönmeyen topacın ki tam olarak aynı görünüyordu. Ve birisi, kütlenin asla değişmeyeceği tahmininde bulunmuştu.
Ne kadar aptalca! Oysa o sadece tahmini olarak ileri sürülmüş bir yasaydı; bir ekstrapolasyondu. O kimse için böyle bilimsel olmayan bir şey yapmıştı? Gerçekte burada bilimsel olmayan bir şey yoktu. sadece olgu kesin değildi. Tersine, tahminde bulunmamak bilimsel olmayan bir tutum sayılacaktı. Tahminde bulunmak zorunluydu. Çünkü extrapolasyon gerçekten bir değere sahip olan tek şeydir. Daha önce denemediğiniz ve hakkında bilgi sahibi olmaya değer bir durumda neler olacağına ilişkin düşüncelerinizin tek ilkesi ekstrapolasyondur. Dün neler olduğuna dair bana söyleyebileceğiniz şeylerin bilgi olarak gerçek bir değeri yoktur. Bilgi, eğer bir şey yapacaksanız, yarın neler olacağını söylemek için gereklidir. - Gerekli de değil fakat eğlenceli. Bunun için sadece boynunuzu dışarıya uzatmaya istekli olmanız gerekecektir.
Her bilimsel yasa, her bilimsel ilke, bir gözlemden elde edilen sonuçların her ifadesi, detayları dışta bırakan bir tür özettir. Çünkü hiçbir şey tüm ayrıntılarıyla ifade edilemez. Topaç örneğindeki adam, sadece yasayı şu şekilde ifade etmesi gerektiğini unutmuştu; "Bir cismin kütlesi, cismin hızı çok yüksek düzeylere çıkmadıkça fazla değişmez."
Oyunun esası, bir spesifik kural yapmak ve sonra da onun süzgeçlerden geçip geçmediğine bakmaktır. Burada spesifik tahmin, bütün durumlarda kütlenin asla değişmeyeceği yönündeydi. Heyecan verici bir olasılık! Bu durumun olmadığının anlaşılmasının zararı yoktur. Çünkü o sadece kesin olmayan bir şeydi ve kesinsiz olmanın zararı yoktur. Bir konuda hiçbir şey söylememektense, emin olmadan birşeyler söylemek daha iyidir.
Gerçek şu ki, bilimde söylediğimiz şeylerin hepsi, varılan sonuçların tümü kesinsizdir, çünkü hepsi sadece sonuçlardır. Onlar gelecekte neler olacağı hakkındaki tahminlerdir ve siz ne olacağını bilemezsiniz. Çünkü çok sayıda eksiksiz deney yapmadınız.
Öte yandan dönmekte olan bir topacın kütlesi üzerindeki bu etki çok küçüktür ve bu nedenle de "Oh, bu etki herhangi bir farklılık yaratmıyor" diyebilirsiniz. Fakat doğru olan ya da en azından ardışık süzgeçlerden geçmeyi sürdüren ve çok daha fazla gözlemle geçerliliğini devam ettiren bir yasa formüle etmek, büyük bir zekayı, imajinasyonu ve felsefemizin, uzay ve zaman anlayışımızın eksiksiz bir şekilde yenileşmesini gerektirir. Ben rölativite teorisine atıfta bulunacağım. Rölativite teorisi, ortaya çıkan zayıf etkilerin, daima çok devrimci düşünce modifikasyonlarını gerektirdiğini göstermiştir.
Bu nedenle bilimciler, şüphe ve kesinsizlikle iş görmeye alışıktırlar. Tüm bilimsel bilgi kesinsizdir. Şüphe ve kesinsizlikle ilgili bu deneyim önemlidir. Ben bu deneyimin çok büyük bir değer taşıdığına ve bilimin ötesinde de genişletilmesi gerektiğine inanıyorum. İnanıyorum ki, daha önce çözülememiş herhangi bir problemi çözmek için, kapıyı bilinmeyene aralık bırakmak zorundasınız. Tam olarak doğru biçimde kestiremediğiniz olasılığa fırsat vermek zorundasınız. Aksi takdirde, eğer zihniniz önceden hazırlarsanız, problemi çözemeyebilirsiniz.
Bir bilimci size problemin cevabını bilmediğini söylediğinde, o bilgisiz bir insandır. Nasıl çalışacağı hakkında bir sezisi olduğunu söylediğinde o konu hakkında kesinsiz durumdadır. Nasıl çalışacağı konusunda tam emin olduğunda ve size "onun çalışma tarzı budur sanıyorum" dediğinde hala bir miktar şüphe içerisindedir. İşte bilgisizlik ve şüphe arasında yaptığımız bu ayırım, gelişme yaratmak için paha biçilmez bir öneme sahiptir. Çünkü biz şüphe duyuyoruz ve o zaman yeni düşünceler için yeni doğrultularda araştırmalar öneriyoruz. Bilimin gelişme hızı, yaptığınız gözlemlerin çokluğu değildir. Çok daha önemlisi, test etmek üzere yeni şeyler yaratmadaki başarınızdır.
Eğer yeni bir yöne bakma arzusu duymamış ya da bu bakışı başaramamış olsaydık, eğer hiç şüphe duymamış ya da bilgisizliği kabul etmemiş olsaydık, yeni fikirlere sahip olamayacaktık. Hiçbir şey kontrol etmeye değer olmayacaktı. Çünkü biz gerçeğin ne olduğunu zaten biliyor olacaktık. Bu nedenle, bizim bu gün bilimsel bilgi olarak adlandırdığımız şey, kesinliğin değişik düzeylerdeki ifadelerinden oluşan bir kümedir. Bunlardan bazıları pak fazla emin olunmayan şeylerdir. Bazıları ise hemen hemen emin olunacak türdendir. Ama bunlardan hiç biri mutlak olarak kesin değildir. Bilimciler buna alışıktır. Biz biliyoruz ki, yaşayabilmek ve bilmemek, birbiriyle uyumludur. Bazı insanlar, "bilmeksizin nasıl yaşayabilirsin?" diyor. Onların ne demek istediklerini bilmiyorum. Ben daima bilmeksizin yaşıyorum. Bu kolay bir şeydir. Neyi bilmek istediğimi nasıl bilebilirsiniz?
Şüphe konusundaki bu özgürlük, bilimde (ve ben inanıyorum ki diğer alanlarda da) önemli bir konudur. Bu bir mücadeleden doğdu. Bu mücadele, şüphe duymaya, emin olmamaya imkan verilmesi mücadelesiydi. Bu mücadelenin önemini ihmalkarlık ederek unutmamızı ve şüphe için özgürlüğün terk edilmesini istemiyorum. Hoşnutluk verici bir bilgisizlik felsefenin büyük değerini ve böyle bir felsefenin mümkün kıldığı ilerlemeyi (ilerleme düşünce özgürlüğünün meyvesidir) bilen bir bilimci olarak sorumluluk hissediyorum.
Bu özgürlüğün değerini açıklamak ve şüphenin korkulacak bir şey olmadığını, tam tersine insanlık için yeni bir potansiyelin olanağı olarak hoşnutlukla karşılanması gerektiğini öğretmek için kendimde bir sorumluluk hissediyorum. Eğer emin olmadığınızı biliyorsanız, durumu değiştirmek için bir şansınız var demektir. Ben bu özgürlüğü gelecek kuşaklar için talep etmek istiyorum.
Şüphe, tüm bilimlerde açık bir değerdir. Onun öteki alanlarda da öyle olup olmadığı, çözümlenmemiş, kesinsiz bir problemdir. Gelecek konferanslarda birçok noktayı tartışmak ve şüphelenmede önemli olanı ve şüphenin endişe edilecek bir şey değil, fakat çok büyük değeri bulunan bir şey olduğunu göstermeye çalışmak için fırsat bulacağımı umuyorum.
(R.Feynman, Her Şeyin Anlamı(1963)Çev: Osman Çeviktay,Evrim yayınları (1999)

 Belirsizlik İlkesi
Belirsizlik İlkesi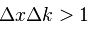
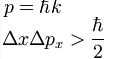
 Dalga boyu uzun
Dalga boyu uzun

