Ziyaretçi
Matematikte karmaşık sayı, bir gerçel bir de sanal kısımdan oluşan bir nesnedir. Karmaşık sayılar şu biçimde gösterilirler
 Genel olarak karmaşık sayılar için "z" harfi kullanılır. a ve b sayıları gerçel olup
Genel olarak karmaşık sayılar için "z" harfi kullanılır. a ve b sayıları gerçel olup  özelliğini sağlayan sanal birime
özelliğini sağlayan sanal birime 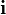 denir. Kimi zaman özellikle elektrik mühendisliğinde
denir. Kimi zaman özellikle elektrik mühendisliğinde 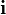 yerine,
yerine,  kullanılır.
kullanılır.
Ayrıca matematikte bu sayıların uzayı olarak gösterilir. Bu harfin seçilmesinin nedeni İngilizce'de karmaşık sözcüğünün karşılığı olarak complex sözcüğünün kullanılmasıdır, nitekim bazı Türkçe kaynaklarda complex sözcüğünden devşirilen kompleks sözcüğüne de raslanabilir. Karmaşık sayılara böyle bir adın verilmesinin nedeni ise aşağıda da göreceğimiz gibi gerçel ve sanal kısımların bir arada durmasıdır.
olarak gösterilir. Bu harfin seçilmesinin nedeni İngilizce'de karmaşık sözcüğünün karşılığı olarak complex sözcüğünün kullanılmasıdır, nitekim bazı Türkçe kaynaklarda complex sözcüğünden devşirilen kompleks sözcüğüne de raslanabilir. Karmaşık sayılara böyle bir adın verilmesinin nedeni ise aşağıda da göreceğimiz gibi gerçel ve sanal kısımların bir arada durmasıdır.
Bütün gerçel sayılar sanal kısımları sıfıra eşit olan birer karmaşık sayı olarak düşünülebilir. Diğer bir deyişle gerçel sayılar, karmaşık sayı düzleminde gerçel sayılar ekseni üzerinde bulunurlar.

Bir z karmaşık sayısının gerçel ve sanal parçaları sırasıyla Re(z) ve Im(z) şeklinde gösterilir. Bütün bu tanımları ve özellikleri bir örnekte gösterelim.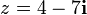
 uzayında bir karmaşık sayıdır. Gerçel sayılar, karmaşık sayıların alt kümesi olduğu için,
uzayında bir karmaşık sayıdır. Gerçel sayılar, karmaşık sayıların alt kümesi olduğu için,  uzayındaki cebrin hepsi dolayısıyla
uzayındaki cebrin hepsi dolayısıyla  uzayında da tanımlıdır. Bunun dışında karmaşık sayıların başka özellikleri de vardır. Örneğin bir karmaşık sayı düzlemde bir vektör olarak temsil edilebilir.
uzayında da tanımlıdır. Bunun dışında karmaşık sayıların başka özellikleri de vardır. Örneğin bir karmaşık sayı düzlemde bir vektör olarak temsil edilebilir.
Tanım
Karmaşık sayılar kümesi birçok şekilde tanımlanabilir. Aşağıdaki tanımların hepsi birbirine eşyapısaldır, yani yapısal olarak biri diğerinin yerine kullanılabilir. Bu yüzden aslında içerik olarak farklı olan aşağıda tanımlanan tüm kümeleri aynı harfle gösterdik, . Ayrıca bu simge, sadece karmaşık sayılar dediğimiz öğeleri içeren bir küme olmaktan ötedir, üzerine tanımlayacağımız iki tane ikili işlemi olan bir cisimdir. Üstelik bu cisim, gerçel sayıların en büyük cisim genişlemesidir, yani gerçel sayıları bundan daha fazla genişletemeyiz. Gerçel sayılarla karmaşık sayıların aynı kardinaliteye (öğe sayısına) sahip olduğunu da unutmayalım.
. Ayrıca bu simge, sadece karmaşık sayılar dediğimiz öğeleri içeren bir küme olmaktan ötedir, üzerine tanımlayacağımız iki tane ikili işlemi olan bir cisimdir. Üstelik bu cisim, gerçel sayıların en büyük cisim genişlemesidir, yani gerçel sayıları bundan daha fazla genişletemeyiz. Gerçel sayılarla karmaşık sayıların aynı kardinaliteye (öğe sayısına) sahip olduğunu da unutmayalım.
Kartezyen uzay tanımı
Gerçel sayılar kümesinde her sayıyı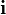 ile çarparsak elde ettiğimiz
ile çarparsak elde ettiğimiz  kümesi önceki
kümesi önceki 

olarak tanımlanmış olur. Bu 2 boyutlu kartezyen uzay, Argand düzlemi olarak anılır. Eğer yerine tamsayılar cismi
yerine tamsayılar cismi  alınırsa oluşan karmaşık tamsayılar Gauss düzlemindedir. Bu sayılara da Gauss sayıları denir.
alınırsa oluşan karmaşık tamsayılar Gauss düzlemindedir. Bu sayılara da Gauss sayıları denir.
Karmaşık sayılar, bu tanımla aşağıdaki gibi ifade edilir: olmak üzere;
olmak üzere;
z = (a,b)
Burada açıkça Re(z) = a ve Im(z) = b dir.
Cisim genişlemesi tanımı
Karmaşık sayılar, gerçel sayılar cisminin bir cisim genişlemesidir.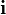 sayısı x2 + 1polinomunun köklerinden biridir ve diğer kökü de
sayısı x2 + 1polinomunun köklerinden biridir ve diğer kökü de 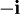 olur. Bu iki öğenin gerçel sayılarla olan genişlemesinin eşyapısal olduğu kolaylıkla görülebilir:
olur. Bu iki öğenin gerçel sayılarla olan genişlemesinin eşyapısal olduğu kolaylıkla görülebilir:

Bu durumda

olarak tanımlanır. Daha açık olarak, karmaşık sayılar gerçel sayılar polinom halkasının x2 + 1 polinomuyla üretilen bölüm halkasıdır:

Bu bölüm halkasında X öğesinin görüntüsü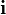 karmaşık birimidir. Bu sayede karmaşık sayılar halkası cebirsel olarak kapalı olur ki bu, gerçel sayıların cebirsel kapanışıdır. Cebirin temel teoremi bunu gerektirir, n dereceli her polinomun tam n kökü vardır. Biz, her karmaşık sayının
karmaşık birimidir. Bu sayede karmaşık sayılar halkası cebirsel olarak kapalı olur ki bu, gerçel sayıların cebirsel kapanışıdır. Cebirin temel teoremi bunu gerektirir, n dereceli her polinomun tam n kökü vardır. Biz, her karmaşık sayının  olarak ifade edildiği bu tanıma daha âşinâyız.
olarak ifade edildiği bu tanıma daha âşinâyız.
Matris (dizey) tanımı
Karmaşık sayıları, gerçel katsayılı 2x2'lik matrislerin bir altkümesi olarak düşünebiliriz. Birim sayıları
 ve
ve 
olarak tanımlanırsa böylece her bir karmaşık sayı

olarak ifade edilebilir ki burada a,b alınmıştır. Kaldı ki
alınmıştır. Kaldı ki

olduğu kolaylıkla görülebilir. O halde karmaşık sayılar

şeklinde tanımlanmış olur.
Karmaşık sayılarda işlem
Karmaşık sayılarda cebirsel işlemler gerçel sayıların genişlemesidir. Öncelikle iki karmaşık sayının eşitliğini verelim.
Eşitlik
Bir ve
ve  karmaşık sayıları için
karmaşık sayıları için
z = w ancak a = c ve b = d iken geçerlidir.
Toplama
Bir ve
ve  karmaşık sayıları için
karmaşık sayıları için

Çarpma
Bir ve
ve  karmaşık sayıları için
karmaşık sayıları için

Eşlenik
Bir karmaşık sayısı için eşlenik ifadesi
karmaşık sayısı için eşlenik ifadesi  dönüşümüdür ve
dönüşümüdür ve

ya da matrislerde

olarak tanımlanır.
Eşleniğin cebirsel özellikleri sayısı gerçel kısmı Re(z) = 4, sanal kısmı Im(z) = − 7 olan kümesine eşyapısaldır. Karmaşık sayılar cismi ise buradan hareketle
Bir karmaşık sayı ile eşleniğinin karmaşık uzaydaki gösterimi.
Mutlak Değer
Bir karmaşık sayısı için
karmaşık sayısı için

ya da

olarak tanımlıdır.
Mutlak değerin cebirsel özellikleri
Bir karmaşık sayısının tersi
karmaşık sayısının tersi
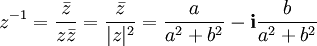
olarak ya da bir matrisin tersine uygun olarak
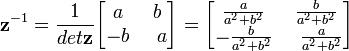
olduğu görülür.
Bölme
Bir ve
ve  karmaşık sayıları için
karmaşık sayıları için

İki tane karmaşık birimi olan ya da bir tane hiperbolik iki tane de karmaşık birimi olan kümeye çifte karmaşık sayılar kümesi denir. Bu kümede her sayı

şeklinde ifade edilebilir. Ancak dörtlük sayılarla karıştırılmamalıdır. Çünkü bu kümede
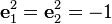
iken

olarak tanımlanır. Zira, bu sayılar dörtlük sayıların değişmelisi olarak anılır.
Bu maddede çifte karmaşık sayı,

olarak gösterilecektir.
Tanım
Çifte karmaşık sayılar birkaç şekilde tanımlanabilir. En yaygın tanımı iki farklı karmaşık sayı kümesinin birleştirimi olduğu için küme çifte karmaşık sıfatını almıştır.
İki karmaşık birim sayı tanımı
İki farklı karmaşık sayı kümesi olduğunu varsayalım: ve
ve  . Her birinin karmaşık birimleri sırasıyla
. Her birinin karmaşık birimleri sırasıyla  ve
ve  olsun. Bu durumda bu iki birimin çarpımı
olsun. Bu durumda bu iki birimin çarpımı

olarak tanımlanır ve bu sayıya 'hiperbolik birim sayı adı verilir. Açık olarak görülür ki bu birim sayı,
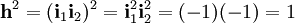
özelliğini sağlar. O halde bir çifte karmaşık sayı

olarak ifade edilebilir.
Karmaşık katsayılı hiperbolik sayı tanımı
Eğer hiperbolik sayı tanımını

gibi karmaşık katsayılı olarak alırsak her çifte karmaşık sayı

şeklinde ifade edilecektir. Burada

olarak tanımlamakla her çifte karmaşık sayıyı

şeklinde ifade etmiş ve istediğimiz özellikleri sağlamış oluruz.
 Genel olarak karmaşık sayılar için "z" harfi kullanılır. a ve b sayıları gerçel olup
Genel olarak karmaşık sayılar için "z" harfi kullanılır. a ve b sayıları gerçel olup  özelliğini sağlayan sanal birime
özelliğini sağlayan sanal birime 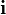 denir. Kimi zaman özellikle elektrik mühendisliğinde
denir. Kimi zaman özellikle elektrik mühendisliğinde 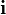 yerine,
yerine,  kullanılır.
kullanılır.Sponsorlu Bağlantılar
Ayrıca matematikte bu sayıların uzayı
 olarak gösterilir. Bu harfin seçilmesinin nedeni İngilizce'de karmaşık sözcüğünün karşılığı olarak complex sözcüğünün kullanılmasıdır, nitekim bazı Türkçe kaynaklarda complex sözcüğünden devşirilen kompleks sözcüğüne de raslanabilir. Karmaşık sayılara böyle bir adın verilmesinin nedeni ise aşağıda da göreceğimiz gibi gerçel ve sanal kısımların bir arada durmasıdır.
olarak gösterilir. Bu harfin seçilmesinin nedeni İngilizce'de karmaşık sözcüğünün karşılığı olarak complex sözcüğünün kullanılmasıdır, nitekim bazı Türkçe kaynaklarda complex sözcüğünden devşirilen kompleks sözcüğüne de raslanabilir. Karmaşık sayılara böyle bir adın verilmesinin nedeni ise aşağıda da göreceğimiz gibi gerçel ve sanal kısımların bir arada durmasıdır.Bütün gerçel sayılar sanal kısımları sıfıra eşit olan birer karmaşık sayı olarak düşünülebilir. Diğer bir deyişle gerçel sayılar, karmaşık sayı düzleminde gerçel sayılar ekseni üzerinde bulunurlar.

Bir z karmaşık sayısının gerçel ve sanal parçaları sırasıyla Re(z) ve Im(z) şeklinde gösterilir. Bütün bu tanımları ve özellikleri bir örnekte gösterelim.
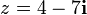
 uzayında bir karmaşık sayıdır. Gerçel sayılar, karmaşık sayıların alt kümesi olduğu için,
uzayında bir karmaşık sayıdır. Gerçel sayılar, karmaşık sayıların alt kümesi olduğu için,  uzayındaki cebrin hepsi dolayısıyla
uzayındaki cebrin hepsi dolayısıyla  uzayında da tanımlıdır. Bunun dışında karmaşık sayıların başka özellikleri de vardır. Örneğin bir karmaşık sayı düzlemde bir vektör olarak temsil edilebilir.
uzayında da tanımlıdır. Bunun dışında karmaşık sayıların başka özellikleri de vardır. Örneğin bir karmaşık sayı düzlemde bir vektör olarak temsil edilebilir.Tanım
Karmaşık sayılar kümesi birçok şekilde tanımlanabilir. Aşağıdaki tanımların hepsi birbirine eşyapısaldır, yani yapısal olarak biri diğerinin yerine kullanılabilir. Bu yüzden aslında içerik olarak farklı olan aşağıda tanımlanan tüm kümeleri aynı harfle gösterdik,
 . Ayrıca bu simge, sadece karmaşık sayılar dediğimiz öğeleri içeren bir küme olmaktan ötedir, üzerine tanımlayacağımız iki tane ikili işlemi olan bir cisimdir. Üstelik bu cisim, gerçel sayıların en büyük cisim genişlemesidir, yani gerçel sayıları bundan daha fazla genişletemeyiz. Gerçel sayılarla karmaşık sayıların aynı kardinaliteye (öğe sayısına) sahip olduğunu da unutmayalım.
. Ayrıca bu simge, sadece karmaşık sayılar dediğimiz öğeleri içeren bir küme olmaktan ötedir, üzerine tanımlayacağımız iki tane ikili işlemi olan bir cisimdir. Üstelik bu cisim, gerçel sayıların en büyük cisim genişlemesidir, yani gerçel sayıları bundan daha fazla genişletemeyiz. Gerçel sayılarla karmaşık sayıların aynı kardinaliteye (öğe sayısına) sahip olduğunu da unutmayalım.Kartezyen uzay tanımı
Gerçel sayılar kümesinde her sayıyı
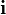 ile çarparsak elde ettiğimiz
ile çarparsak elde ettiğimiz  kümesi önceki
kümesi önceki 

olarak tanımlanmış olur. Bu 2 boyutlu kartezyen uzay, Argand düzlemi olarak anılır. Eğer
 yerine tamsayılar cismi
yerine tamsayılar cismi  alınırsa oluşan karmaşık tamsayılar Gauss düzlemindedir. Bu sayılara da Gauss sayıları denir.
alınırsa oluşan karmaşık tamsayılar Gauss düzlemindedir. Bu sayılara da Gauss sayıları denir.Karmaşık sayılar, bu tanımla aşağıdaki gibi ifade edilir:
 olmak üzere;
olmak üzere;z = (a,b)
Burada açıkça Re(z) = a ve Im(z) = b dir.
Cisim genişlemesi tanımı
Karmaşık sayılar, gerçel sayılar cisminin bir cisim genişlemesidir.
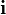 sayısı x2 + 1polinomunun köklerinden biridir ve diğer kökü de
sayısı x2 + 1polinomunun köklerinden biridir ve diğer kökü de 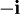 olur. Bu iki öğenin gerçel sayılarla olan genişlemesinin eşyapısal olduğu kolaylıkla görülebilir:
olur. Bu iki öğenin gerçel sayılarla olan genişlemesinin eşyapısal olduğu kolaylıkla görülebilir: 
Bu durumda

olarak tanımlanır. Daha açık olarak, karmaşık sayılar gerçel sayılar polinom halkasının x2 + 1 polinomuyla üretilen bölüm halkasıdır:

Bu bölüm halkasında X öğesinin görüntüsü
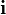 karmaşık birimidir. Bu sayede karmaşık sayılar halkası cebirsel olarak kapalı olur ki bu, gerçel sayıların cebirsel kapanışıdır. Cebirin temel teoremi bunu gerektirir, n dereceli her polinomun tam n kökü vardır. Biz, her karmaşık sayının
karmaşık birimidir. Bu sayede karmaşık sayılar halkası cebirsel olarak kapalı olur ki bu, gerçel sayıların cebirsel kapanışıdır. Cebirin temel teoremi bunu gerektirir, n dereceli her polinomun tam n kökü vardır. Biz, her karmaşık sayının  olarak ifade edildiği bu tanıma daha âşinâyız.
olarak ifade edildiği bu tanıma daha âşinâyız.Matris (dizey) tanımı
Karmaşık sayıları, gerçel katsayılı 2x2'lik matrislerin bir altkümesi olarak düşünebiliriz. Birim sayıları
 ve
ve 
olarak tanımlanırsa böylece her bir karmaşık sayı

olarak ifade edilebilir ki burada a,b
 alınmıştır. Kaldı ki
alınmıştır. Kaldı ki
olduğu kolaylıkla görülebilir. O halde karmaşık sayılar

şeklinde tanımlanmış olur.
Karmaşık sayılarda işlem
Karmaşık sayılarda cebirsel işlemler gerçel sayıların genişlemesidir. Öncelikle iki karmaşık sayının eşitliğini verelim.
Eşitlik
Bir
 ve
ve  karmaşık sayıları için
karmaşık sayıları içinz = w ancak a = c ve b = d iken geçerlidir.
Toplama
Bir
 ve
ve  karmaşık sayıları için
karmaşık sayıları için
Çarpma
Bir
 ve
ve  karmaşık sayıları için
karmaşık sayıları için
Eşlenik
Bir
 karmaşık sayısı için eşlenik ifadesi
karmaşık sayısı için eşlenik ifadesi  dönüşümüdür ve
dönüşümüdür ve
ya da matrislerde

olarak tanımlanır.
Eşleniğin cebirsel özellikleri sayısı gerçel kısmı Re(z) = 4, sanal kısmı Im(z) = − 7 olan kümesine eşyapısaldır. Karmaşık sayılar cismi ise buradan hareketle




 ancak z gerçel sayı olduğunda geçerlidir.
ancak z gerçel sayı olduğunda geçerlidir.

Bir karmaşık sayı ile eşleniğinin karmaşık uzaydaki gösterimi.
Mutlak Değer
Bir
 karmaşık sayısı için
karmaşık sayısı için
ya da

olarak tanımlıdır.
Mutlak değerin cebirsel özellikleri
 ancak
ancak  iken geçerlidir.
iken geçerlidir.
 (üçgen eşitsizliği)
(üçgen eşitsizliği)
Bir
 karmaşık sayısının tersi
karmaşık sayısının tersi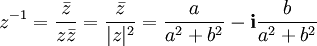
olarak ya da bir matrisin tersine uygun olarak
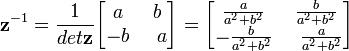
olduğu görülür.
Bölme
Bir
 ve
ve  karmaşık sayıları için
karmaşık sayıları için
İki tane karmaşık birimi olan ya da bir tane hiperbolik iki tane de karmaşık birimi olan kümeye çifte karmaşık sayılar kümesi denir. Bu kümede her sayı

şeklinde ifade edilebilir. Ancak dörtlük sayılarla karıştırılmamalıdır. Çünkü bu kümede
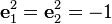
iken

olarak tanımlanır. Zira, bu sayılar dörtlük sayıların değişmelisi olarak anılır.
Bu maddede çifte karmaşık sayı,

olarak gösterilecektir.
Tanım
Çifte karmaşık sayılar birkaç şekilde tanımlanabilir. En yaygın tanımı iki farklı karmaşık sayı kümesinin birleştirimi olduğu için küme çifte karmaşık sıfatını almıştır.
İki karmaşık birim sayı tanımı
İki farklı karmaşık sayı kümesi olduğunu varsayalım:
 ve
ve  . Her birinin karmaşık birimleri sırasıyla
. Her birinin karmaşık birimleri sırasıyla  ve
ve  olsun. Bu durumda bu iki birimin çarpımı
olsun. Bu durumda bu iki birimin çarpımı
olarak tanımlanır ve bu sayıya 'hiperbolik birim sayı adı verilir. Açık olarak görülür ki bu birim sayı,
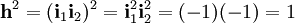
özelliğini sağlar. O halde bir çifte karmaşık sayı

olarak ifade edilebilir.
Karmaşık katsayılı hiperbolik sayı tanımı
Eğer hiperbolik sayı tanımını

gibi karmaşık katsayılı olarak alırsak her çifte karmaşık sayı

şeklinde ifade edilecektir. Burada

olarak tanımlamakla her çifte karmaşık sayıyı

şeklinde ifade etmiş ve istediğimiz özellikleri sağlamış oluruz.
Vikipedi, özgür ansiklopedi

 Karmaşık Sayı
Karmaşık Sayı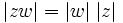
 {z} ile gösterilir. z 'yi, z'nin gerçel kısmına gönderen karmaşık fonksiyon holomorfik değildir.
{z} ile gösterilir. z 'yi, z'nin gerçel kısmına gönderen karmaşık fonksiyon holomorfik değildir. kullanıldığında, z'nin gerçel kısmı
kullanıldığında, z'nin gerçel kısmı  ifadesine eşit olur.
ifadesine eşit olur.
 gibi ayrılabilir. Burada i sayısı sanal birimdir. Bu geleneksel gösterimde z karmaşık sayısı, kartezyen düzlemindeki (x, y) sayısına karşılık gelmektedir. Kartezyen düzleminde (x, y) ayrıca kutupsal koordinatlar kulllanılarak
gibi ayrılabilir. Burada i sayısı sanal birimdir. Bu geleneksel gösterimde z karmaşık sayısı, kartezyen düzlemindeki (x, y) sayısına karşılık gelmektedir. Kartezyen düzleminde (x, y) ayrıca kutupsal koordinatlar kulllanılarak olarak ifade edilebilir.
olarak ifade edilebilir. Bu denklemde,
Bu denklemde,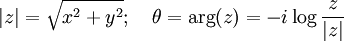 eşitlikleri alınmıştır.[4]
eşitlikleri alınmıştır.[4]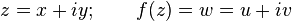 olarak yazılır ve f, z-düzleminin ((x, y) koordinatlarıyla) w-düzlemine ((u, v) koordinatlarıyla) dönüşümü olarak düşünülür.
olarak yazılır ve f, z-düzleminin ((x, y) koordinatlarıyla) w-düzlemine ((u, v) koordinatlarıyla) dönüşümü olarak düşünülür. ilişkisini göz önüne alalım. Bu ilişkiyi tek değerli bir fonksiyon olarak incelemeden önce, sonuç değerinin görüntüsü bir şekilde sınırlandırılmış olmalıdır. Gerçel sayıların karekökleriyle uğraşırken bu yapılan çok kolaydır. Mesela, y2 = x olacak şekilde
ilişkisini göz önüne alalım. Bu ilişkiyi tek değerli bir fonksiyon olarak incelemeden önce, sonuç değerinin görüntüsü bir şekilde sınırlandırılmış olmalıdır. Gerçel sayıların karekökleriyle uğraşırken bu yapılan çok kolaydır. Mesela, y2 = x olacak şekilde ifadesinde negatif olmayan bir y sayısı tanımlanabilir. Ancak, bu fikir iki boyutlu karmaşık düzlemde iyi bir fikir değildir. Neden olduğunu görmek için, z değeri birim çember üzerinde hareket ettikçe f(z)'nin değerinin nasıl değiştiğine bakalım.
ifadesinde negatif olmayan bir y sayısı tanımlanabilir. Ancak, bu fikir iki boyutlu karmaşık düzlemde iyi bir fikir değildir. Neden olduğunu görmek için, z değeri birim çember üzerinde hareket ettikçe f(z)'nin değerinin nasıl değiştiğine bakalım. ifadesini yazabiliriz.
ifadesini yazabiliriz.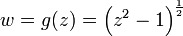 ilişkisini ele alalım. Burada z2 − 1 polinomu z = ±1 değerlerinde 0 değerini alır ve böylece g 'nin açıkça iki dallanma noktası olur. Düzlemi gerçel eksen boyunca, −1 'den 1 'e kadar, "kesebiliriz" ve g(z) 'nin tekdeğerli olduğu bir yaprak elde edebiliriz. Alternatif bir kesim ise z = 1 noktasından sonsuz noktasına kadar pozitif gerçel eksen boyunca gidilip sonra bu sonsuz noktasından z = −1 noktasına negatif gerçel eksen boyunca gidilerek yapılabilir.
ilişkisini ele alalım. Burada z2 − 1 polinomu z = ±1 değerlerinde 0 değerini alır ve böylece g 'nin açıkça iki dallanma noktası olur. Düzlemi gerçel eksen boyunca, −1 'den 1 'e kadar, "kesebiliriz" ve g(z) 'nin tekdeğerli olduğu bir yaprak elde edebiliriz. Alternatif bir kesim ise z = 1 noktasından sonsuz noktasına kadar pozitif gerçel eksen boyunca gidilip sonra bu sonsuz noktasından z = −1 noktasına negatif gerçel eksen boyunca gidilerek yapılabilir.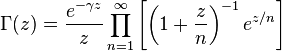 şeklinde tanımlanan gama fonksiyonunun (burada, γ, Euler-Mascheroni sabitidir) 0, −1, −2, −3, ... noktalarında basit kutupları vardır çünkü z sıfır olduğunda veya negatif bir tamsayı olduğunda, sonsuz çarpımdaki paydalardan kesinlikle birisi 0 olmaktadır.[9] Tüm kutupları negatif gerçel eksen üzerinde z = 0 'dan sonsuza kadar sıralandığı için, bu fonksiyon
şeklinde tanımlanan gama fonksiyonunun (burada, γ, Euler-Mascheroni sabitidir) 0, −1, −2, −3, ... noktalarında basit kutupları vardır çünkü z sıfır olduğunda veya negatif bir tamsayı olduğunda, sonsuz çarpımdaki paydalardan kesinlikle birisi 0 olmaktadır.[9] Tüm kutupları negatif gerçel eksen üzerinde z = 0 'dan sonsuza kadar sıralandığı için, bu fonksiyon sonsuz serisi tarafından tanımlanan fonksiyonu göz önüne alalım. Her karmaşık z sayısı için z2 = (−z)2 olduğu için, f(z), z 'nin çift fonksiyonu olacaktır. Böylece, analiz karmaşık düzlemin bir yarısında yeterli olacaktır. Seri
sonsuz serisi tarafından tanımlanan fonksiyonu göz önüne alalım. Her karmaşık z sayısı için z2 = (−z)2 olduğu için, f(z), z 'nin çift fonksiyonu olacaktır. Böylece, analiz karmaşık düzlemin bir yarısında yeterli olacaktır. Seri olduğunda tanımsız olduğu için, düzlem sanal eksen boyunca kesilir ve z 'nin gerçel kısmının 0 olmadığı yerde serinin yakınsaklığı kurulur. [10]
olduğunda tanımsız olduğu için, düzlem sanal eksen boyunca kesilir ve z 'nin gerçel kısmının 0 olmadığı yerde serinin yakınsaklığı kurulur. [10] ele alınsın. f(z) ancak ve ancak z, z < −¼ 'ü sağlayan negatif bir gerçel sayı olmadıkça sonlu bir sayıya yakınsar. Başka bir deyişle, bu sürekli kesir için yakınsaklık bölgesi kesiğin negatif gerçel eksen boyunca −¼ 'ten sonsuza kadar uzandığı kesik düzlemdir.[11]
ele alınsın. f(z) ancak ve ancak z, z < −¼ 'ü sağlayan negatif bir gerçel sayı olmadıkça sonlu bir sayıya yakınsar. Başka bir deyişle, bu sürekli kesir için yakınsaklık bölgesi kesiğin negatif gerçel eksen boyunca −¼ 'ten sonsuza kadar uzandığı kesik düzlemdir.[11] fonksiyonunun f 'nin tanım kümesini iki bağlantısız yaprağa bölerek nasıl tek değerli hale getirilebildiği yukarıda anlatılmıştı. Aynı zamanda, bu iki yaprağı tekrar "yapıştırıp", üzerinde f(z) = z½ fonksiyonun holomorfik olduğu ve fonksiyonun görüntüsünün (w = 0 noktası dışında) tüm w-düzlemi olduğu bir Riemann yüzeyi oluşturulabilir. Bu, şu şekilde yapılmaktadır:
fonksiyonunun f 'nin tanım kümesini iki bağlantısız yaprağa bölerek nasıl tek değerli hale getirilebildiği yukarıda anlatılmıştı. Aynı zamanda, bu iki yaprağı tekrar "yapıştırıp", üzerinde f(z) = z½ fonksiyonun holomorfik olduğu ve fonksiyonun görüntüsünün (w = 0 noktası dışında) tüm w-düzlemi olduğu bir Riemann yüzeyi oluşturulabilir. Bu, şu şekilde yapılmaktadır: olduğunu gösterir. Bundan, f 'nin türevinin var olduğunu ve türevin Riemann yüzeyi üzerindeki z = 0 dışında her yerde sonlu olduğunu çıkarabiliriz (yani, f, z = 0 dışında holomorfiktir).
olduğunu gösterir. Bundan, f 'nin türevinin var olduğunu ve türevin Riemann yüzeyi üzerindeki z = 0 dışında her yerde sonlu olduğunu çıkarabiliriz (yani, f, z = 0 dışında holomorfiktir).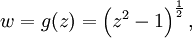 fonksiyonu Riemann yüzeyi için oluşturulabilir? Yeniden, z-düzleminin iki kopyasıyla başlarız; ancak bu sefer her birisi gerçel doğru parçası boyunca, z = −1 'den z = 1 'e, kesilir bunlar g(z) 'nin iki dallanma noktası olur. Bunlardan birisini yine yukarıdan aşağıya çeviririz ve böylece sanal eksenler ters yönlü olurlar. İki yaprağın karşılık gelen kenarları tekrar birleştirilir. g 'nin bu yüzey üzerinde tek değerli olduğu z = 1 merkezli birim yarıçaplı bir çember üzerinde döngü yapılarak doğrulanabilir. Birinci yapraktaki z = 2 noktasından başlanır ve z = 0 'daki kesikle karşılaşmadan çember etrafında yarım dönülür. Bu kesik bizi ikinci yaprağa gitmeye zorlar böylece z, z = 1 dallanma noktası etrafında bir tam döngü, w ise bir yarım döngü yapmıştır. w 'nun işareti terse döndürülmüştür (eiπ = −1 olduğundan) ve yolumuz bizi yüzeyin ikinci yaprağındaki z = 2 noktasına götürmüştür. Başka bir yarım tur daha yaptığımızda, z = 0 olduğu kesiğin diğer tarafıyla karşılaşırız ve son olarak başlangıç noktamıza ( birinci yapraktaki z = 2 noktasına) dallanma noktasının etrafında iki tam döngü yaptıktan sonra ulaşırız.
fonksiyonu Riemann yüzeyi için oluşturulabilir? Yeniden, z-düzleminin iki kopyasıyla başlarız; ancak bu sefer her birisi gerçel doğru parçası boyunca, z = −1 'den z = 1 'e, kesilir bunlar g(z) 'nin iki dallanma noktası olur. Bunlardan birisini yine yukarıdan aşağıya çeviririz ve böylece sanal eksenler ters yönlü olurlar. İki yaprağın karşılık gelen kenarları tekrar birleştirilir. g 'nin bu yüzey üzerinde tek değerli olduğu z = 1 merkezli birim yarıçaplı bir çember üzerinde döngü yapılarak doğrulanabilir. Birinci yapraktaki z = 2 noktasından başlanır ve z = 0 'daki kesikle karşılaşmadan çember etrafında yarım dönülür. Bu kesik bizi ikinci yaprağa gitmeye zorlar böylece z, z = 1 dallanma noktası etrafında bir tam döngü, w ise bir yarım döngü yapmıştır. w 'nun işareti terse döndürülmüştür (eiπ = −1 olduğundan) ve yolumuz bizi yüzeyin ikinci yaprağındaki z = 2 noktasına götürmüştür. Başka bir yarım tur daha yaptığımızda, z = 0 olduğu kesiğin diğer tarafıyla karşılaşırız ve son olarak başlangıç noktamıza ( birinci yapraktaki z = 2 noktasına) dallanma noktasının etrafında iki tam döngü yaptıktan sonra ulaşırız. {z} ile gösterilir. z 'yi, z'nin sanal kısmına gönderen karmaşık fonksiyon holomorfik değildir.
{z} ile gösterilir. z 'yi, z'nin sanal kısmına gönderen karmaşık fonksiyon holomorfik değildir. ifadesine eşit olur.
ifadesine eşit olur.
