1.Fermat'nin Son Teoremi
Fransız matematikçi Pierre de Fermat'nın 17. yüzyılda öne sürdüğü fakat kanıtı ancak 1994 yılında İngiliz matematikçi Andrew Wiles tarafından verilen teoremdir.
İfadesinin ortaokul matematik bilgileriyle anlaşılacak kadar yalın olmasına karşılık öne sürülmesiyle kanıtlanması arasında geçen çok uzun sürede pek çok ünlü matematikçi tarafından üzerinde uğraşılıp da kanıtlanamamış olmasıyla matematik tarihinde öne çıkmıştır.
Kısaca, eğer n ikiden büyük bir tamsayıysa, ve x, y, z sayıları pozitif tamsayılar ise
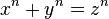 ifadesinin sağlanamayacağını ifade eder. İfadenin n=1 ve n=2 durumlarında kolayca sağlanabileceğini görmek zor değildir. Biraz açmak gerekirse, n=2 durumu ünlüPisagor Teoremi ile yakından ilişkili olup x=3, y=4, z=5 veya x=5, y=12, z=13 tamsayı üçlüleriyle kolayca sağlanır.
ifadesinin sağlanamayacağını ifade eder. İfadenin n=1 ve n=2 durumlarında kolayca sağlanabileceğini görmek zor değildir. Biraz açmak gerekirse, n=2 durumu ünlüPisagor Teoremi ile yakından ilişkili olup x=3, y=4, z=5 veya x=5, y=12, z=13 tamsayı üçlüleriyle kolayca sağlanır.
Bu sanının (artık teorem demek gerekiyor elbette) kanıtı için pek çok matematikçi uğraşmış ancak başarısız olmuşlardır. Ancak yakın tarihlere kadar çok büyük n değerleri için bu sanının doğrulanmasına devam edilmiştir. Bu tür kısmi ilerlemelere yönelik çabalar, hiç beklenmedik bir zamanda İngiliz matematikçi Andrew Wiles'ın bir kanıt bulduğunu duyurmasıyla son bulmuştur. Ne var ki kısa sürede Andrew Wiles'ın kanıtında bir hata bulunmuş ve Andrew Wiles uzun ve yorucu bir çabanın sonunda 1994 yılında uzmanlarca doğruluğu kabul gören bir kanıt vermeyi başarmıştır. Aslında Wiles'ın kanıtı Fermat'nın son teoreminden daha güçlü bir ifadenin, Şimura-Taniyama Konjektürü'nün de doğruluğunu göstermiştir. Söz konusu kanıt Sayılar Teorisi'nin çok gelişkin tekniklerini kullanır.
2.Riemann Hipotezi
Riemann Hipotezi (Riemann zeta hipotezi olarak da bilinmektedir),matematik alanında ilk kez 1859 yılında Bernhard Riemann tarafından formülize edilmiş çözülememiş problemlerden biridir.
Bazı sayıların kendilerinden küçük sayıların çarpımı (örn. 2, 3, 5, 7, ...) cinsinden yazılamamak gibi bir özelliği vardır. Bu tür sayılara Asal sayılar denir. Asal sayılar, hem matematik hem de uygulama alanlarında çok önemli rol oynar. Asal sayıların tüm doğal sayılar içinde dağılımı herhangi bir örüntüyü takip etmemektedir ancak Alman matematikçi Bernhard Riemann, Asal sayıların sıklığının;
s ≠ 1 olmak koşuluyla tüm Kompleks sayılar için
ζ(s) = 1 + 1/2s + 1/3s + 1/4s + ...
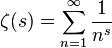 biçiminde belirtilen ve Riemann Zeta Fonksiyonu olarak bilinen fonksiyonun davranışına çok bağlı olduğunu gözlemledi. Riemann hipotezinin iddiasına göre
biçiminde belirtilen ve Riemann Zeta Fonksiyonu olarak bilinen fonksiyonun davranışına çok bağlı olduğunu gözlemledi. Riemann hipotezinin iddiasına göre
ζ(s) = 0
denkleminin tüm çözümleri düz bir çizgi üzerinde yer almaktadır. Yani bu denkleminin tüm komplex çözümlerinin reel kısımlarının 1/2 olduğu tahmin edilmektedir. Bu iddia ilk 1.500.000.000 çözüm için test edilmiştir. Bu iddianın her çözüm için doğru olduğunun ispatlanabilmesi halinde asal sayıların dağılımı ile ilgili çok önemli bilgiler edinmek mümkün olacaktır.
3.Goldbach Hipotezi
Sayılar teorisindeki en eski Matematikte çözümsüz problemlerden biridir. Sanı: Goldbach'ın orijinal sanısı (üçül varsayım) Euler'e 7 Haziran 1742'de yazdığı mektupta şöyle ifade ediliyor:
...En azından 2'den büyük her sayı üç asal sayının toplamıdır...
Goldbach burada 1 sayısını da asal kabul etmektedir. (Bu konvansiyon artık terkedilmiştir.) (1 sayısı niçin asal değildir?: Çünkü bir asal sayı başka bir asal sayıyı asla tam bölmez. Oysa 1 sayısı diğer asalları da tam böler.)
Kuvvetli ikil varsayım, 3'ten büyük her çift doğal sayının iki asal sayının toplamı olarak ifade edilebileceğini öne sürer. Faber and Faber adlı yayın şirketi bu sanının doğru olduğunu 20 Mart 2000 ve 20 Mart 2002 arasındaki 2 yıllık sürede kanıtlayabilecek ilk kişiye 1.000.000 Amerıkan doları ödül vaadetmiştir, fakat sanı halen ispatsız olduğu üzere bu ödülü de kazanan olmamıştır.
İkil sanı şöyledir:
 ve
ve  için
için  olacak şekilde
olacak şekilde  ve
ve  asal sayıları vardır. (
asal sayıları vardır. ( olabilir)
olabilir)
Her bir Goldbach bölüntüsü olarak adlandırılır. Daha zayıf olan ikinci sanı sadece 8'den büyük olan her tek doğal sayının en az 3 asal sayının toplamı olduğudur. Erdös ve Moser
bir Goldbach bölüntüsü olarak adlandırılır. Daha zayıf olan ikinci sanı sadece 8'den büyük olan her tek doğal sayının en az 3 asal sayının toplamı olduğudur. Erdös ve Moser  ve
ve  'nin asal olma koşulunu kaldırarak bu sanının daha genel anlamda doğru olup olmadığını araştırmışlardır.
'nin asal olma koşulunu kaldırarak bu sanının daha genel anlamda doğru olup olmadığını araştırmışlardır.
4.Cantor'un Köşegen Yöntemi
Georg Cantor'un doğal sayılar ile reel sayıların birebir eşlemesinin yapılamayacağını göstermek için geliştirdiği yöntem. Böyle bir eşlemenin yokluğu sonsuz elemanlı kümelerin büyüklüklerinin karşılaştırılması kavramının gelişimi açısından son derece önemlidir.
Büyüklük
Verilen bir A kümesinin en az B kümesi kadar büyük olması B'den A'ya bir birebir fonksiyonun var olması şeklinde tanımlanır ( yazılır). Böylelikle B'nin bir kopyasının A'nın içersinde bulunabiliyor olması sağlanır. Eğer aynı şekilde B'den de A'ya bir birebir fonksiyon varsa o zaman bu iki küme eşit büyüklükte denir (
yazılır). Böylelikle B'nin bir kopyasının A'nın içersinde bulunabiliyor olması sağlanır. Eğer aynı şekilde B'den de A'ya bir birebir fonksiyon varsa o zaman bu iki küme eşit büyüklükte denir ( yazılır).
yazılır).
Reel sayıların sonlu veya sonsuz uzunlukta ondalık sayılar olarak yazılabileceği bilinir. Diyelim ki Cantor'un iddiası yanlış ve de reel sayılarla doğal sayılar birebir eşlenebiliyor. O zaman sadece 0 la 1 arasındaki reel sayılarla (bütün) doğal sayıları birebir eşlemek de mümkündür. Böyle bir eşlemeyi alalım ve 0 la 1 arasındaki reel sayıları verilen eşlemeye göre sıralayarak bir liste elde edelim. Şimdi 0 la 1 arasında öyle bir reel sayı kurgulayacağız ki bu sayının bu listede yer alması mümkün olmayacak. Bu sayıya C adını verelim ve onu şu kurala göre oluşturalım: birinci sayının ilk ondalık basamağına bakalım ve buradaki rakamdan farklı herhangi bir rakamı seçip C sayısının ilk basamağı olarak yazalım, aynı şekilde C'nin ikinci, üçüncü,... basamaklarını da oluşturalım. Mesela eğer 0 la 1 arasındaki reel sayılar aşağıdaki gibi sıralanmışsa:
1) 0,13567.......
^
2) 0,25678.......
^
3) 0,00212.......
^
4) 0,14221.......
^
.
.
.
C sayısının ilk basamağını 1'den farklı, 2. basamağını 5'ten farklı, 3. basamağını 2'den farklı, 4. basamağını gene 2'den farklı birer rakam olarak seçeriz.
Bu noktada fark etmemiz gereken şey, C'nin kendisi bir reel sayı olduğu halde bu listede yer alan her sayıdan en az bir ondalık basamakta (daha doğrusu o sayı listemizde kaçıncı sırada yer alıyorsa o basamakta) farklı olduğu ve dolayısıyla bu listede yer alamayacağı. Demek ki varsaydığımız birebir eşleme mümkün değil ve aslında reel sayılar kümesindeki eleman sayısı doğal sayılar kümesindeki eleman sayısından daha fazla.
5.Pisagor Teoremi
Pisagor teoremine göre bir diküçgende dik kenarların karelerinin toplamları hipotenüsün karesine eşittir.
Bunun ispatı şuna dayanmaktadır:
c2 = a2 + b2 c uzunluğu hipotenüstür. a ve b uzunlukları ise dik kenarlardır. Her kenardan birer kare oluşturulur. bu karelerin alanları, kare alan formülüne dayalı olarak a2,b2,c2 şeklinde sıralanır. böylece üç karenin köşelerinin birleşiminden oluşan bir dik üçgen oluşturulur. Oluşan üçgenin dik köşesinden hipotenüsün oluşturduğu karenin, hipotenüse paralel olan kenara indirilen dikme ile üçgen içerisinde öklid bağıntısı kurulur. (öklid bağıntısı benzerlikten ispatlanabilmektedir.) Öklide göre
a2 = p(p + q)
yani, dik kenarlardan birinin karesi, dik açıdan hipotenüse indirilen dikmenin ayırdığı parçalardan kendisine komşu olan tarafın uzunluğu ile hipotenüsün tamamının çarpımına eşittir. Bu durumda
a2 = p.c
olacaktır. Yani a kenarına ait karenin alanı, hipotenüse ait alanın dik açıdan indirilen dikmeyle ikiye ayırdığı alanlardan kendisine komşu olan alana eşit olacaktır. Bu durumu diğer kenar için de düşünürüz.
a2 = p.(p + q)b2 = q.(p + q)
p + q = c
a2 = p.c,b2 = q.c olacaktır. Bunu takiben,
a2 + b2 = p.c + q.c
a2 + b2 = c.(p + q)
p + q = c
a2 + b2 = c.c
a2 + b2 = c2
olacaktır.
Matematikte, Pisagor Teoremi, Öklid geometrisinde bir dik üçgenin 3 kenarı için bir bağıntıdır. Bilinen en eski matematiksel teoremlerden biridir. Teorem sonradan İÖ 6. YY'da Yunan filozof ve matematikçi Pisagor'a atfen isimlendirilmiş ise de, Hindu, Yunan, Çnli ve Babilli matematikçiler teoremin unsurlarını, o yaşamadan önce bilmekteydiler.
Pisagor teoreminin bilinen ilk ispatı Öklid'in Elementler eserinde bulunabilir.

Pisagor teoreminin animasyonlu geometrik

Pisagor bağıntısı görsel açıklaması
Sayısal Örnek ve Tarihte Kullanılışı
En yaygin olarak karşılaşılan örneklerden biri "3-4-5" üçgenidir. (32 + 42 = 52)
Bu, komşu kenarları sırasıyla 3 birim, 4 birim ve karşı kenarı 5 birim olan bir dik üçgeni temsil eder.
Diğer örnekleri ise 5-12-13, 8-15-17, 7-24-25, 9-40-41 ...
Aslında köklü uzunluğu olmayan bir dik üçgen elde etmek için formul vardır:
Pisagor teoremi bir dik açı oluşturmak için kullanılabilir. Şöyle ki:
1) Yeterli uzunlukta bir halatı(ya da ipliği) eşit 12 parçaya ayıracak şekilde işaretleyin.
2) Bu işaretlerden 3üncü ve 5inci(3+5) noktalari sabitleyip, ipin acikta kalan iki ucunu (gergin olacak şekilde) birleştirin.
3) 3üncü işaretin bulundugu noktada bir dik açı elde edersiniz.
Bu yöntemin gecmişte tarım alanlarının paylaşılması, arazi sınırlarının belirlenmesi gibi alanlarda kullanıldıgı bilinmektedir...
6. İkiz Asallar Sanısı
Aralarındaki fark 2 olan asal sayılara ikiz asal sayılar denir. (örneğin 3 ve 5, 5 ve 7, 11 ve 13 .. ikiz asallardır.) (2,3) çifti hariç iki asal sayının arasındaki fark da zaten en az 2 olabilir.
İkiz asalların sonsuz tane olmasına ilişkin soru, sayılar kuramının yılladır çözülememiş en büyük problemlerinden birisidir ve "ikiz asallar sanısı ( varsayımı,kestirimi) olarak adlandırılır. "Hardy-Littlewood sanısı" ikiz asalların dağılımı üzerine " asal sayılar teoremi" ne benzer bir varsayımda bulunur.
Viggo Brun , ünlü " eleme metoduyla" bir x sayısından küçük ikiz asal sayıların sayısının , x/(log)2 den küçük olduğunu göstermiştir. Bu sonuç da bütün ikiz asal sayı çiftler toplamının yakınsak olduğunu göstermektedir (bakınız Brun sabiti).Bu tüm asal sayı çiftlerinin toplamının ıraksadığına terstir (p ve p' asal sayılar ve k bir doğal sayı olmak üzere p-p'=2k , bu genellemeden k=1 için ikiz asallar varsayımına gidilir ; bahsi geçen tüm asal sayı çiftlerin toplamı k değişken olmak üzere p ve p' lerin toplamıdır). Brun ayrıca her çift sayının , en fazla 9 tane asal çarpanı olan iki tane sayının farkı olarak sonsuz biçimde ifade edilebileceğini göstermiştir. Chen Jingrun'un ünlü teoremi göstermektedir ki herhangi bir m çift sayısı için m ile aralarında en fazla 2 tane asal çarpanı olan bir sayı kadar fark olan asal sayılardan sonsuz tane vardır.
3 ten büyük her ikiz asal sayı çifti ,bazı n doğal sayıları için , ( 6n-1 , 6n +1 )şeklinde ifade edilir. Öyleki n , 1 'e eşit değildir ve 0,2,3,5,7 veya 8 ile sonlanmak zorundadır.
m ve m+2 sayı çifti ancak ve ancak
 durumunda bir ikiz asal sayı çiftidir.
durumunda bir ikiz asal sayı çiftidir.
2005 yılına gelindiğinde bilinen en büyük ikiz asal sayı çifti 16869987339975 · 2171960 ± 1 dir. Macar Zoltán Járai, Gabor Farkas, Timea Csajbok, Janos Kasza ve Antal Járai tarafından 2005 yılında bulunmuş olup 51779 haneli sayılardır.
4.35 · 1015 e değin yapılan tüm asal sayı çiflerin deneysel analizi göstermektedir ki x den az çift sayısı x·f(x)/(log x)2 dir. Burada f(x) küçük değerli x ler için yaklaşık 1.7 dir ve x sonsuza giderken yaklaşık 1.3 e kadar azalır. f(x) 'in limit değeri "ikiz asal sabiti" ne eşit olduğu varsayılmaktadır.

Bu varsayım ikiz asallar sanısını gerektirmektedir ki hâlâ çözümsüzdür.
İlk 35 ikiz asal çifti
(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571), (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883)
7. Cebirin Temel Teoremi
[°â¹] şeklindeki karmaşık katsayılı bir polinomun kökleri, p(x) polinomu içersinde x bilinmeyeni yerine konduğunda 0 sonucu veren değerlerdir. Cebirin Temel Teoremi sabit olmayan (yani derecesi en az bir olan) kompleks katsayılı her p(x) polinomu için en az bir kompleks kök olduğunu ifade eder.
şeklindeki karmaşık katsayılı bir polinomun kökleri, p(x) polinomu içersinde x bilinmeyeni yerine konduğunda 0 sonucu veren değerlerdir. Cebirin Temel Teoremi sabit olmayan (yani derecesi en az bir olan) kompleks katsayılı her p(x) polinomu için en az bir kompleks kök olduğunu ifade eder.
8.Gödel'in Eksiklik Teoremi
Gödel'in çağdaşı olan ünlü matematikçi Hilbert, matematikteki tüm ispatların, belli bir yöntemle, yani aksiyomatik bir sistem vasıtasıyla, elde edilebileceğini düşünüyordu ve bu doğrultuda çalışmalarına başladı. Temel aritmetikteki tüm doğruları, aksiyomlarından türetebilirse, matematikteki tüm doğruları da bu aksiyomlardan elde edebilecekti.
Gödel bunun olanaksızlığını gösterdi. Bunu kısaca şu şekilde yaptı: Bu önerme ispatlanamaz ifadesini aritmetik sisteminde formülize etti. Aynı şekilde G ifadenin değilini (Bu önerme ispatlanabilir) de formülize etti. Daha sonra, G ifadesinin aritmetik olarak doğruluğu hesaplanabilirse, G ifadesinin değilinin de doğruluğunun hesaplanabileceğini gösterdi. Ve Gödel buradan şu iki sonuca varmıştır:
1. Elementer aritmetik içeren aksiyomatik bir sistem tutarlı (consistent) ise eksiksiz (complete) değildir.
2. Elementer aritmetik içeren aksiyomatik bir sistemin tutarlılığını sistemin kendi içinden (sistemin kendi formüllerini ve işlemlerini kullanarak) ispatlamak mümkün değildir.
İşin ilginç tarafı, bu G ifadesi sistemin içine bir aksiyom olarak yerleştirilse bile, yeni bir Gödel cümlesi çıkartılabilir. Yani ne kadar aksiyom eklersek ekleyelim, böyle bir sistemde doğruluğu ya da yanlışlığı ispatlanamayacak bir Gödel cümlesi bulunacaktır.
9. Dört Renk Teoremi
Sonlu sayıda bölgeden oluşan bir harita, birbirine sonsuz sayıda nokta boyunca komşu olan iki bölgenin renkleri birbirinden farklı olmak üzere, boyanacaksa bu işlem için dört rengin yeterli olacağı bir strateji vardır.
Bu teoremin doğrudan uygulamalarından birisi harita boyanmasıdır; eğer her ülkenin tek bölgeden oluştuğu varsayılırsa bir siyasi haritanın tüm ülkeleri, komşu ülkeler aynı renge boyanmadan dört renge boyanabilir. Ancak bu uygulamadaki varsayım, dünya haritası için uygun olmayıp Amerika Birleşik Devletleri ve Azerbaycan gibi birden fazla bölgeden oluşan ülkeler bulunmaktadır.
Bu konjektür (ispatsız, fakat doğruluğu tahmin edilen sanı) 1852'de Augustus De Morgan'ın bir öğrencisi olan Francis Guthrie tarafından ileri sürüldü; fakat ancak 1976'da Appel ve Haken tarafından bilgisayarla kanıtlandı. Matematik tarihinde bu bir bilgisayarın ispatladığı ilk teoremdir.

Dört Renk Teoremi'nin bir örnek
10. Hesabın Temel Teoremi
Kabaca türev almakla integral alma işlemlerinin birbirinin tersi olduğunu ifade eden teoremdir. En basit şekliyle

formülüyle ifade edilebilir. Burada c herhangi bir sabit sayıdır ve integral alma işlemini gösteren
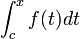
ifadesini, eksenlerini t ve y harfleriyle gösterdiğimiz 2 boyutlu kartezyen uzayda, t = c, t = x doğruları ve y = f(t) eğrisiyle t-ekseni arasında kalan bölgenin alanını hesaplama işlemi olarak düşünmemiz gerekir. Kolaylık olsun diye f(t) 'nin negatif değerler almadığını varsaydığımıza dikkat etmek gerekir.
11. P ile NP Arasındaki İlişki
P harfi "polynomial", NP harfleri ise "non-deterministic polynomial" ifadelerini temsil eder, türkçe karşılıkları "polinom" ve "belirleyici olmayan polinom"dur. "P eşittir NP?" ise Hesaplama Teorisi'nin en temel ve meşhur problemidir.
Polinomsal zamanda çözülen problemler
Hesaplama teorisinde, bazı tip problemlerin çözümü için en etkili algoritmaların çalışma süresinin girilen verinin büyüklüğüne bir polinom cinsinden bağlı olduğu bilinmektedir (buna polinomsal zamanda çalışan algoritma adı verilir), bu tür problemler P kategorisindeki problemlerdir. Mesela verilen basamaklı bir sayının asal olup olmadığını kontrol etmek için çalışma süresi
basamaklı bir sayının asal olup olmadığını kontrol etmek için çalışma süresi  mertebesinde bir polinomla hesaplanabilen bir algoritma vardır. Dolayısıyla verilen bir sayının asal olup olmadığının araştırılması P kategorisinde bir problemdir.
mertebesinde bir polinomla hesaplanabilen bir algoritma vardır. Dolayısıyla verilen bir sayının asal olup olmadığının araştırılması P kategorisinde bir problemdir.
Polinomsal zamanda çözülemeyen problemler
Buna karşılık bir diğer grup problem vardır ki bunlar için sorulan soruya girilen verinin büyüklüğüne polinom mertebesinde bağımlı bir sürede cevap verecek bir algoritma bilinmemektedir. Fakat bu tür bazı problemler için eğer bir şekilde cevabı tahmin edebiliyorsak, tahminimizin doğruluğunu sınamak için veri büyüklüğüne polinom mertebesinde bağımlı sürelerde çalışacak algoritmalar vardır. Bu tür problemler, yani bir tahminin doğruluğunun kontrolü için çalışma süresi verinin büyüklüğüne polinom cinsinden bağımlı bir algoritma olan problemler de NP kategorisini oluştururlar. Örnek olarak verilen basamaklı bir sayının asal çarpanlarının neler olduğu sorusunu düşünebiliriz. Bu sorunun cevabı için bilinen en iyi algoritmanın çalışma süresi
basamaklı bir sayının asal çarpanlarının neler olduğu sorusunu düşünebiliriz. Bu sorunun cevabı için bilinen en iyi algoritmanın çalışma süresi  sayısına bir polinom cinsinden değil de eksponansiyel fonksiyonlar cinsinden (
sayısına bir polinom cinsinden değil de eksponansiyel fonksiyonlar cinsinden ( misali) bağımlıdır (buna üstel zamanda çalışan algoritma denir), fakat bu problem için eğer bir şekilde cevabı tahmin edebiliyorsak tahminimizin doğruluğunu sınamak için
misali) bağımlıdır (buna üstel zamanda çalışan algoritma denir), fakat bu problem için eğer bir şekilde cevabı tahmin edebiliyorsak tahminimizin doğruluğunu sınamak için  sayısına polinom mertebesinde bağımlı bir sürede çalışacak bir algoritma mevcuttur. Dolayısıyla verilen bir n basamaklı sayının asal çarpanlarının neler olduğu sorusu NP kategorisindedir.
sayısına polinom mertebesinde bağımlı bir sürede çalışacak bir algoritma mevcuttur. Dolayısıyla verilen bir n basamaklı sayının asal çarpanlarının neler olduğu sorusu NP kategorisindedir.
P ve NP arasındaki bağ
Bu iki kategoriden NP'nin P'yi içerdiğini görmek kolaydır. Eğer bir sorunun cevabını verinin büyüklüğüne polinom mertebesinde bağımlı sürede çalışacak bir algoritmayla bulabiliyorsak, bu soruya cevap olarak üretilmiş bir tahminin doğruluğunu da verinin büyüklüğüne polinom mertebesinde bağımlı sürede çalışacak bir algoritmayla kontrol edebiliriz. Bunun için verilen sorunun cevabını verecek algoritmayı çalıştırıp, onun verdiği cevabı kendi tahminimizle karşılaştırmak yeterlidir. "P=NP?" problemi bunun tersinin de doğru olup olmadığını sorar. Yani NP kategorisinde olup da P kategorisinde olmayan problemler var mıdır? Veya diğer bir dille asal çarpanların bulunması için polinom mertebesinde bir sürede çalışacak bir algoritma gerçekten yok mu yoksa var da biz mi bulamıyoruz? Bu alanın uzmanlarının çoğunun görüşü bu tür algoritmaların gerçekten de var olmadıkları için bulunamadığı (yani P nin NP'ye eşit olmadığı) şeklinde ancak bu soruya kesin bir cevap verilebilmesi şimdilik çok zor gözüküyor.
12. Aritmetiğin Temel Teoremi
Her doğal sayının sonlu sayıda asal sayının kuvvetlerinin çarpımı olarak yazılabileceğini ifade eden teorem. İspatını ilk olarak Öklid yapmıştır.
Kanıtı
Bu teorem'in ispatı, teoremin gerçek olmadığını varsayıp bunun bir çelişkiye yol açacağını göstererek yapılmıştır. Diyelim ki "n" bu teorimi çürütecek olan en küçük doğal sayı olsun. Asal olmadığına göre, n=ab şeklinde yazılabilir ve a ve b n ile 1 arasında birer doğal sayı'dır. Fakat n bu teorimi çürütecek en küçük sayı olduğundan, a ve b birer asal sayının çarpımı olarak yazılabilir. Ancak bu durumda, n de asal sayıların çarpımıdır, ve bu yüzden ilk varsayım gerçek olamaz. Bu n'in varolamayacağını gösterir ve teorimimizi ispatlar.
13. Bolzano-Weierstrass Teoremi
Bolzano-Weierstrass teoremi klasik matematik analizin temel teoremlerinden biridir. İlk kez "Fonksiyonlar" adlı kitabında Bernhard Bolzano tarafından kullanıldı. Sonraki yıllarda bu teoremin ispatı tam olarak Karl Weierstrass tarafından verilmiştir. Bu nedenle, bu teorem analizde Bolzano-Weierstrass teoremi olarak bilinir.
 , reel sayılar kümesinin, sınırlı ve sonsuz elemana sahip her alt kümesinin en az bir yığılma noktası vardır.
, reel sayılar kümesinin, sınırlı ve sonsuz elemana sahip her alt kümesinin en az bir yığılma noktası vardır.
ispat:
reel sayılarda sınırlı ve sonsuz elemanlı bir küme A olsun. Reel sayılar tamlık aksiyomunu sağladığından A kümesinin supremum ve infimum'u vardır. infA=x, supA=y olsun. Bu durumda her aЄA için x≤a≤y elde edilir. [x,y] aralığını iki kapalı aralığa bölelim. Bu aralıklardan en az bir tanesi sonsuz eleman kapsar. Böylece devam edilerek tümevarımla artan(xn) ve azalan , xn<yn dizilerini oluştururuz. [xn,yn] aralığının uzunluğu yn-xn=y-x/2n ve A∩[xn,yn] kümesinin sonsuz çoklukta elemanı vardır. (xn) artan sınırlı, azalan sınırlı dizi olduklarından yakınsar. limnxn=supnxn=p ve limnyn=infnyn=q olsun. yn-xn=y-x/2n olduğundan supnxn=infnyn=p olur. ε>0 verilsin. y-x<y-x/2n olacak biçimde nЄN seçelim. bu durumda yn-p≤yn-xn<ε ve p-xn≤yn-xn<ε elde edilir. (p-ε,p+ε)aralığı A∩[xn,yn] kümesinin sonsuz çoklukta elemanını kapsadığından p noktası A kümesinin bir yığılma noktasıdır.
14. Ceva Teoremi
Ceva Teoremi, Bir ABC üçgeninde D, E ve F sırasıyla BC, CA ve AB doğru parçaları üzerindeki noktalar olmak kaydı ile AD, BE ve CF doğru parçalarının aynı noktada kesişmeleri için gerek ve yeter koşul şöyle yazılabilir:
BD.CE.AF = DE.EA.FB
Bu durum söz konusu olan doğru parçaları kenarortay, açıortay veya yükseklik olduğunda da geçerlidir.
15. Fermat'ın Küçük Teoremi
Fermat'ın küçük teoremi p asal sayı ise ve obeb(p,a)=1 yani a ve p aralarında asal ise

olduğunu belirten teoremdir.
Teorem asallık testlerinde ve bilgisayarda büyük sayılarla işlemlerde kullanılır.
16. Thales teoremi
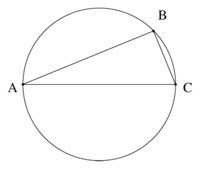
Thales Teoremi: AC çap ise, B dik açıdır
16-Thales Teoremi, birbirine benzer iki çokgen arasında kurulmuş bağıntıdır. Geometrinin gelişmesine katkıda bulunmuştur. Hatta trigonometri ile hesaplanmış ama ispatlanmamış bazı özel durumların ispatındada Thales Teoremi kullanılmıştır.
Sponsorlu Bağlantılar
İfadesinin ortaokul matematik bilgileriyle anlaşılacak kadar yalın olmasına karşılık öne sürülmesiyle kanıtlanması arasında geçen çok uzun sürede pek çok ünlü matematikçi tarafından üzerinde uğraşılıp da kanıtlanamamış olmasıyla matematik tarihinde öne çıkmıştır.
Kısaca, eğer n ikiden büyük bir tamsayıysa, ve x, y, z sayıları pozitif tamsayılar ise
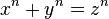 ifadesinin sağlanamayacağını ifade eder. İfadenin n=1 ve n=2 durumlarında kolayca sağlanabileceğini görmek zor değildir. Biraz açmak gerekirse, n=2 durumu ünlüPisagor Teoremi ile yakından ilişkili olup x=3, y=4, z=5 veya x=5, y=12, z=13 tamsayı üçlüleriyle kolayca sağlanır.
ifadesinin sağlanamayacağını ifade eder. İfadenin n=1 ve n=2 durumlarında kolayca sağlanabileceğini görmek zor değildir. Biraz açmak gerekirse, n=2 durumu ünlüPisagor Teoremi ile yakından ilişkili olup x=3, y=4, z=5 veya x=5, y=12, z=13 tamsayı üçlüleriyle kolayca sağlanır.Bu sanının (artık teorem demek gerekiyor elbette) kanıtı için pek çok matematikçi uğraşmış ancak başarısız olmuşlardır. Ancak yakın tarihlere kadar çok büyük n değerleri için bu sanının doğrulanmasına devam edilmiştir. Bu tür kısmi ilerlemelere yönelik çabalar, hiç beklenmedik bir zamanda İngiliz matematikçi Andrew Wiles'ın bir kanıt bulduğunu duyurmasıyla son bulmuştur. Ne var ki kısa sürede Andrew Wiles'ın kanıtında bir hata bulunmuş ve Andrew Wiles uzun ve yorucu bir çabanın sonunda 1994 yılında uzmanlarca doğruluğu kabul gören bir kanıt vermeyi başarmıştır. Aslında Wiles'ın kanıtı Fermat'nın son teoreminden daha güçlü bir ifadenin, Şimura-Taniyama Konjektürü'nün de doğruluğunu göstermiştir. Söz konusu kanıt Sayılar Teorisi'nin çok gelişkin tekniklerini kullanır.
2.Riemann Hipotezi
Riemann Hipotezi (Riemann zeta hipotezi olarak da bilinmektedir),matematik alanında ilk kez 1859 yılında Bernhard Riemann tarafından formülize edilmiş çözülememiş problemlerden biridir.
Bazı sayıların kendilerinden küçük sayıların çarpımı (örn. 2, 3, 5, 7, ...) cinsinden yazılamamak gibi bir özelliği vardır. Bu tür sayılara Asal sayılar denir. Asal sayılar, hem matematik hem de uygulama alanlarında çok önemli rol oynar. Asal sayıların tüm doğal sayılar içinde dağılımı herhangi bir örüntüyü takip etmemektedir ancak Alman matematikçi Bernhard Riemann, Asal sayıların sıklığının;
s ≠ 1 olmak koşuluyla tüm Kompleks sayılar için
ζ(s) = 1 + 1/2s + 1/3s + 1/4s + ...
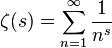 biçiminde belirtilen ve Riemann Zeta Fonksiyonu olarak bilinen fonksiyonun davranışına çok bağlı olduğunu gözlemledi. Riemann hipotezinin iddiasına göre
biçiminde belirtilen ve Riemann Zeta Fonksiyonu olarak bilinen fonksiyonun davranışına çok bağlı olduğunu gözlemledi. Riemann hipotezinin iddiasına göreζ(s) = 0
denkleminin tüm çözümleri düz bir çizgi üzerinde yer almaktadır. Yani bu denkleminin tüm komplex çözümlerinin reel kısımlarının 1/2 olduğu tahmin edilmektedir. Bu iddia ilk 1.500.000.000 çözüm için test edilmiştir. Bu iddianın her çözüm için doğru olduğunun ispatlanabilmesi halinde asal sayıların dağılımı ile ilgili çok önemli bilgiler edinmek mümkün olacaktır.
3.Goldbach Hipotezi
Sayılar teorisindeki en eski Matematikte çözümsüz problemlerden biridir. Sanı: Goldbach'ın orijinal sanısı (üçül varsayım) Euler'e 7 Haziran 1742'de yazdığı mektupta şöyle ifade ediliyor:
...En azından 2'den büyük her sayı üç asal sayının toplamıdır...
Goldbach burada 1 sayısını da asal kabul etmektedir. (Bu konvansiyon artık terkedilmiştir.) (1 sayısı niçin asal değildir?: Çünkü bir asal sayı başka bir asal sayıyı asla tam bölmez. Oysa 1 sayısı diğer asalları da tam böler.)
Kuvvetli ikil varsayım, 3'ten büyük her çift doğal sayının iki asal sayının toplamı olarak ifade edilebileceğini öne sürer. Faber and Faber adlı yayın şirketi bu sanının doğru olduğunu 20 Mart 2000 ve 20 Mart 2002 arasındaki 2 yıllık sürede kanıtlayabilecek ilk kişiye 1.000.000 Amerıkan doları ödül vaadetmiştir, fakat sanı halen ispatsız olduğu üzere bu ödülü de kazanan olmamıştır.
İkil sanı şöyledir:
 ve
ve  için
için  olacak şekilde
olacak şekilde  ve
ve  asal sayıları vardır. (
asal sayıları vardır. ( olabilir)
olabilir)Her
 bir Goldbach bölüntüsü olarak adlandırılır. Daha zayıf olan ikinci sanı sadece 8'den büyük olan her tek doğal sayının en az 3 asal sayının toplamı olduğudur. Erdös ve Moser
bir Goldbach bölüntüsü olarak adlandırılır. Daha zayıf olan ikinci sanı sadece 8'den büyük olan her tek doğal sayının en az 3 asal sayının toplamı olduğudur. Erdös ve Moser  ve
ve  'nin asal olma koşulunu kaldırarak bu sanının daha genel anlamda doğru olup olmadığını araştırmışlardır.
'nin asal olma koşulunu kaldırarak bu sanının daha genel anlamda doğru olup olmadığını araştırmışlardır. 4.Cantor'un Köşegen Yöntemi
Georg Cantor'un doğal sayılar ile reel sayıların birebir eşlemesinin yapılamayacağını göstermek için geliştirdiği yöntem. Böyle bir eşlemenin yokluğu sonsuz elemanlı kümelerin büyüklüklerinin karşılaştırılması kavramının gelişimi açısından son derece önemlidir.
Büyüklük
Verilen bir A kümesinin en az B kümesi kadar büyük olması B'den A'ya bir birebir fonksiyonun var olması şeklinde tanımlanır (
 yazılır). Böylelikle B'nin bir kopyasının A'nın içersinde bulunabiliyor olması sağlanır. Eğer aynı şekilde B'den de A'ya bir birebir fonksiyon varsa o zaman bu iki küme eşit büyüklükte denir (
yazılır). Böylelikle B'nin bir kopyasının A'nın içersinde bulunabiliyor olması sağlanır. Eğer aynı şekilde B'den de A'ya bir birebir fonksiyon varsa o zaman bu iki küme eşit büyüklükte denir ( yazılır).
yazılır).- Örnek olarak Çift Tam Sayılar Kümesi'nin (
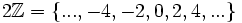 ) ile Tam Sayılar Kümesi
) ile Tam Sayılar Kümesi 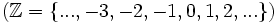 düşünülebilir.
düşünülebilir.  'nin elemanları
'nin elemanları  'nin içersinde kendi kendilerine gönderilir.
'nin içersinde kendi kendilerine gönderilir.
Reel sayıların sonlu veya sonsuz uzunlukta ondalık sayılar olarak yazılabileceği bilinir. Diyelim ki Cantor'un iddiası yanlış ve de reel sayılarla doğal sayılar birebir eşlenebiliyor. O zaman sadece 0 la 1 arasındaki reel sayılarla (bütün) doğal sayıları birebir eşlemek de mümkündür. Böyle bir eşlemeyi alalım ve 0 la 1 arasındaki reel sayıları verilen eşlemeye göre sıralayarak bir liste elde edelim. Şimdi 0 la 1 arasında öyle bir reel sayı kurgulayacağız ki bu sayının bu listede yer alması mümkün olmayacak. Bu sayıya C adını verelim ve onu şu kurala göre oluşturalım: birinci sayının ilk ondalık basamağına bakalım ve buradaki rakamdan farklı herhangi bir rakamı seçip C sayısının ilk basamağı olarak yazalım, aynı şekilde C'nin ikinci, üçüncü,... basamaklarını da oluşturalım. Mesela eğer 0 la 1 arasındaki reel sayılar aşağıdaki gibi sıralanmışsa:
1) 0,13567.......
^
2) 0,25678.......
^
3) 0,00212.......
^
4) 0,14221.......
^
.
.
.
C sayısının ilk basamağını 1'den farklı, 2. basamağını 5'ten farklı, 3. basamağını 2'den farklı, 4. basamağını gene 2'den farklı birer rakam olarak seçeriz.
Bu noktada fark etmemiz gereken şey, C'nin kendisi bir reel sayı olduğu halde bu listede yer alan her sayıdan en az bir ondalık basamakta (daha doğrusu o sayı listemizde kaçıncı sırada yer alıyorsa o basamakta) farklı olduğu ve dolayısıyla bu listede yer alamayacağı. Demek ki varsaydığımız birebir eşleme mümkün değil ve aslında reel sayılar kümesindeki eleman sayısı doğal sayılar kümesindeki eleman sayısından daha fazla.
5.Pisagor Teoremi
Pisagor teoremine göre bir diküçgende dik kenarların karelerinin toplamları hipotenüsün karesine eşittir.
Bunun ispatı şuna dayanmaktadır:
c2 = a2 + b2 c uzunluğu hipotenüstür. a ve b uzunlukları ise dik kenarlardır. Her kenardan birer kare oluşturulur. bu karelerin alanları, kare alan formülüne dayalı olarak a2,b2,c2 şeklinde sıralanır. böylece üç karenin köşelerinin birleşiminden oluşan bir dik üçgen oluşturulur. Oluşan üçgenin dik köşesinden hipotenüsün oluşturduğu karenin, hipotenüse paralel olan kenara indirilen dikme ile üçgen içerisinde öklid bağıntısı kurulur. (öklid bağıntısı benzerlikten ispatlanabilmektedir.) Öklide göre
a2 = p(p + q)
yani, dik kenarlardan birinin karesi, dik açıdan hipotenüse indirilen dikmenin ayırdığı parçalardan kendisine komşu olan tarafın uzunluğu ile hipotenüsün tamamının çarpımına eşittir. Bu durumda
a2 = p.c
olacaktır. Yani a kenarına ait karenin alanı, hipotenüse ait alanın dik açıdan indirilen dikmeyle ikiye ayırdığı alanlardan kendisine komşu olan alana eşit olacaktır. Bu durumu diğer kenar için de düşünürüz.
a2 = p.(p + q)b2 = q.(p + q)
p + q = c
a2 = p.c,b2 = q.c olacaktır. Bunu takiben,
a2 + b2 = p.c + q.c
a2 + b2 = c.(p + q)
p + q = c
a2 + b2 = c.c
a2 + b2 = c2
olacaktır.
Matematikte, Pisagor Teoremi, Öklid geometrisinde bir dik üçgenin 3 kenarı için bir bağıntıdır. Bilinen en eski matematiksel teoremlerden biridir. Teorem sonradan İÖ 6. YY'da Yunan filozof ve matematikçi Pisagor'a atfen isimlendirilmiş ise de, Hindu, Yunan, Çnli ve Babilli matematikçiler teoremin unsurlarını, o yaşamadan önce bilmekteydiler.
Pisagor teoreminin bilinen ilk ispatı Öklid'in Elementler eserinde bulunabilir.

Pisagor teoreminin animasyonlu geometrik

Pisagor bağıntısı görsel açıklaması
Sayısal Örnek ve Tarihte Kullanılışı
En yaygin olarak karşılaşılan örneklerden biri "3-4-5" üçgenidir. (32 + 42 = 52)
Bu, komşu kenarları sırasıyla 3 birim, 4 birim ve karşı kenarı 5 birim olan bir dik üçgeni temsil eder.
Diğer örnekleri ise 5-12-13, 8-15-17, 7-24-25, 9-40-41 ...
Aslında köklü uzunluğu olmayan bir dik üçgen elde etmek için formul vardır:
Pisagor teoremi bir dik açı oluşturmak için kullanılabilir. Şöyle ki:
1) Yeterli uzunlukta bir halatı(ya da ipliği) eşit 12 parçaya ayıracak şekilde işaretleyin.
2) Bu işaretlerden 3üncü ve 5inci(3+5) noktalari sabitleyip, ipin acikta kalan iki ucunu (gergin olacak şekilde) birleştirin.
3) 3üncü işaretin bulundugu noktada bir dik açı elde edersiniz.
Bu yöntemin gecmişte tarım alanlarının paylaşılması, arazi sınırlarının belirlenmesi gibi alanlarda kullanıldıgı bilinmektedir...
6. İkiz Asallar Sanısı
Aralarındaki fark 2 olan asal sayılara ikiz asal sayılar denir. (örneğin 3 ve 5, 5 ve 7, 11 ve 13 .. ikiz asallardır.) (2,3) çifti hariç iki asal sayının arasındaki fark da zaten en az 2 olabilir.
İkiz asalların sonsuz tane olmasına ilişkin soru, sayılar kuramının yılladır çözülememiş en büyük problemlerinden birisidir ve "ikiz asallar sanısı ( varsayımı,kestirimi) olarak adlandırılır. "Hardy-Littlewood sanısı" ikiz asalların dağılımı üzerine " asal sayılar teoremi" ne benzer bir varsayımda bulunur.
Viggo Brun , ünlü " eleme metoduyla" bir x sayısından küçük ikiz asal sayıların sayısının , x/(log)2 den küçük olduğunu göstermiştir. Bu sonuç da bütün ikiz asal sayı çiftler toplamının yakınsak olduğunu göstermektedir (bakınız Brun sabiti).Bu tüm asal sayı çiftlerinin toplamının ıraksadığına terstir (p ve p' asal sayılar ve k bir doğal sayı olmak üzere p-p'=2k , bu genellemeden k=1 için ikiz asallar varsayımına gidilir ; bahsi geçen tüm asal sayı çiftlerin toplamı k değişken olmak üzere p ve p' lerin toplamıdır). Brun ayrıca her çift sayının , en fazla 9 tane asal çarpanı olan iki tane sayının farkı olarak sonsuz biçimde ifade edilebileceğini göstermiştir. Chen Jingrun'un ünlü teoremi göstermektedir ki herhangi bir m çift sayısı için m ile aralarında en fazla 2 tane asal çarpanı olan bir sayı kadar fark olan asal sayılardan sonsuz tane vardır.
3 ten büyük her ikiz asal sayı çifti ,bazı n doğal sayıları için , ( 6n-1 , 6n +1 )şeklinde ifade edilir. Öyleki n , 1 'e eşit değildir ve 0,2,3,5,7 veya 8 ile sonlanmak zorundadır.
m ve m+2 sayı çifti ancak ve ancak
 durumunda bir ikiz asal sayı çiftidir.
durumunda bir ikiz asal sayı çiftidir.2005 yılına gelindiğinde bilinen en büyük ikiz asal sayı çifti 16869987339975 · 2171960 ± 1 dir. Macar Zoltán Járai, Gabor Farkas, Timea Csajbok, Janos Kasza ve Antal Járai tarafından 2005 yılında bulunmuş olup 51779 haneli sayılardır.
4.35 · 1015 e değin yapılan tüm asal sayı çiflerin deneysel analizi göstermektedir ki x den az çift sayısı x·f(x)/(log x)2 dir. Burada f(x) küçük değerli x ler için yaklaşık 1.7 dir ve x sonsuza giderken yaklaşık 1.3 e kadar azalır. f(x) 'in limit değeri "ikiz asal sabiti" ne eşit olduğu varsayılmaktadır.

Bu varsayım ikiz asallar sanısını gerektirmektedir ki hâlâ çözümsüzdür.
İlk 35 ikiz asal çifti
(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571), (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883)
7. Cebirin Temel Teoremi
[°â¹]
 şeklindeki karmaşık katsayılı bir polinomun kökleri, p(x) polinomu içersinde x bilinmeyeni yerine konduğunda 0 sonucu veren değerlerdir. Cebirin Temel Teoremi sabit olmayan (yani derecesi en az bir olan) kompleks katsayılı her p(x) polinomu için en az bir kompleks kök olduğunu ifade eder.
şeklindeki karmaşık katsayılı bir polinomun kökleri, p(x) polinomu içersinde x bilinmeyeni yerine konduğunda 0 sonucu veren değerlerdir. Cebirin Temel Teoremi sabit olmayan (yani derecesi en az bir olan) kompleks katsayılı her p(x) polinomu için en az bir kompleks kök olduğunu ifade eder.8.Gödel'in Eksiklik Teoremi
Gödel'in çağdaşı olan ünlü matematikçi Hilbert, matematikteki tüm ispatların, belli bir yöntemle, yani aksiyomatik bir sistem vasıtasıyla, elde edilebileceğini düşünüyordu ve bu doğrultuda çalışmalarına başladı. Temel aritmetikteki tüm doğruları, aksiyomlarından türetebilirse, matematikteki tüm doğruları da bu aksiyomlardan elde edebilecekti.
Gödel bunun olanaksızlığını gösterdi. Bunu kısaca şu şekilde yaptı: Bu önerme ispatlanamaz ifadesini aritmetik sisteminde formülize etti. Aynı şekilde G ifadenin değilini (Bu önerme ispatlanabilir) de formülize etti. Daha sonra, G ifadesinin aritmetik olarak doğruluğu hesaplanabilirse, G ifadesinin değilinin de doğruluğunun hesaplanabileceğini gösterdi. Ve Gödel buradan şu iki sonuca varmıştır:
1. Elementer aritmetik içeren aksiyomatik bir sistem tutarlı (consistent) ise eksiksiz (complete) değildir.
2. Elementer aritmetik içeren aksiyomatik bir sistemin tutarlılığını sistemin kendi içinden (sistemin kendi formüllerini ve işlemlerini kullanarak) ispatlamak mümkün değildir.
İşin ilginç tarafı, bu G ifadesi sistemin içine bir aksiyom olarak yerleştirilse bile, yeni bir Gödel cümlesi çıkartılabilir. Yani ne kadar aksiyom eklersek ekleyelim, böyle bir sistemde doğruluğu ya da yanlışlığı ispatlanamayacak bir Gödel cümlesi bulunacaktır.
9. Dört Renk Teoremi
Sonlu sayıda bölgeden oluşan bir harita, birbirine sonsuz sayıda nokta boyunca komşu olan iki bölgenin renkleri birbirinden farklı olmak üzere, boyanacaksa bu işlem için dört rengin yeterli olacağı bir strateji vardır.
Bu teoremin doğrudan uygulamalarından birisi harita boyanmasıdır; eğer her ülkenin tek bölgeden oluştuğu varsayılırsa bir siyasi haritanın tüm ülkeleri, komşu ülkeler aynı renge boyanmadan dört renge boyanabilir. Ancak bu uygulamadaki varsayım, dünya haritası için uygun olmayıp Amerika Birleşik Devletleri ve Azerbaycan gibi birden fazla bölgeden oluşan ülkeler bulunmaktadır.
Bu konjektür (ispatsız, fakat doğruluğu tahmin edilen sanı) 1852'de Augustus De Morgan'ın bir öğrencisi olan Francis Guthrie tarafından ileri sürüldü; fakat ancak 1976'da Appel ve Haken tarafından bilgisayarla kanıtlandı. Matematik tarihinde bu bir bilgisayarın ispatladığı ilk teoremdir.

Dört Renk Teoremi'nin bir örnek
10. Hesabın Temel Teoremi
Kabaca türev almakla integral alma işlemlerinin birbirinin tersi olduğunu ifade eden teoremdir. En basit şekliyle

formülüyle ifade edilebilir. Burada c herhangi bir sabit sayıdır ve integral alma işlemini gösteren
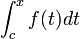
ifadesini, eksenlerini t ve y harfleriyle gösterdiğimiz 2 boyutlu kartezyen uzayda, t = c, t = x doğruları ve y = f(t) eğrisiyle t-ekseni arasında kalan bölgenin alanını hesaplama işlemi olarak düşünmemiz gerekir. Kolaylık olsun diye f(t) 'nin negatif değerler almadığını varsaydığımıza dikkat etmek gerekir.
11. P ile NP Arasındaki İlişki
P harfi "polynomial", NP harfleri ise "non-deterministic polynomial" ifadelerini temsil eder, türkçe karşılıkları "polinom" ve "belirleyici olmayan polinom"dur. "P eşittir NP?" ise Hesaplama Teorisi'nin en temel ve meşhur problemidir.
Polinomsal zamanda çözülen problemler
Hesaplama teorisinde, bazı tip problemlerin çözümü için en etkili algoritmaların çalışma süresinin girilen verinin büyüklüğüne bir polinom cinsinden bağlı olduğu bilinmektedir (buna polinomsal zamanda çalışan algoritma adı verilir), bu tür problemler P kategorisindeki problemlerdir. Mesela verilen
 basamaklı bir sayının asal olup olmadığını kontrol etmek için çalışma süresi
basamaklı bir sayının asal olup olmadığını kontrol etmek için çalışma süresi  mertebesinde bir polinomla hesaplanabilen bir algoritma vardır. Dolayısıyla verilen bir sayının asal olup olmadığının araştırılması P kategorisinde bir problemdir.
mertebesinde bir polinomla hesaplanabilen bir algoritma vardır. Dolayısıyla verilen bir sayının asal olup olmadığının araştırılması P kategorisinde bir problemdir.Polinomsal zamanda çözülemeyen problemler
Buna karşılık bir diğer grup problem vardır ki bunlar için sorulan soruya girilen verinin büyüklüğüne polinom mertebesinde bağımlı bir sürede cevap verecek bir algoritma bilinmemektedir. Fakat bu tür bazı problemler için eğer bir şekilde cevabı tahmin edebiliyorsak, tahminimizin doğruluğunu sınamak için veri büyüklüğüne polinom mertebesinde bağımlı sürelerde çalışacak algoritmalar vardır. Bu tür problemler, yani bir tahminin doğruluğunun kontrolü için çalışma süresi verinin büyüklüğüne polinom cinsinden bağımlı bir algoritma olan problemler de NP kategorisini oluştururlar. Örnek olarak verilen
 basamaklı bir sayının asal çarpanlarının neler olduğu sorusunu düşünebiliriz. Bu sorunun cevabı için bilinen en iyi algoritmanın çalışma süresi
basamaklı bir sayının asal çarpanlarının neler olduğu sorusunu düşünebiliriz. Bu sorunun cevabı için bilinen en iyi algoritmanın çalışma süresi  sayısına bir polinom cinsinden değil de eksponansiyel fonksiyonlar cinsinden (
sayısına bir polinom cinsinden değil de eksponansiyel fonksiyonlar cinsinden ( misali) bağımlıdır (buna üstel zamanda çalışan algoritma denir), fakat bu problem için eğer bir şekilde cevabı tahmin edebiliyorsak tahminimizin doğruluğunu sınamak için
misali) bağımlıdır (buna üstel zamanda çalışan algoritma denir), fakat bu problem için eğer bir şekilde cevabı tahmin edebiliyorsak tahminimizin doğruluğunu sınamak için  sayısına polinom mertebesinde bağımlı bir sürede çalışacak bir algoritma mevcuttur. Dolayısıyla verilen bir n basamaklı sayının asal çarpanlarının neler olduğu sorusu NP kategorisindedir.
sayısına polinom mertebesinde bağımlı bir sürede çalışacak bir algoritma mevcuttur. Dolayısıyla verilen bir n basamaklı sayının asal çarpanlarının neler olduğu sorusu NP kategorisindedir.P ve NP arasındaki bağ
Bu iki kategoriden NP'nin P'yi içerdiğini görmek kolaydır. Eğer bir sorunun cevabını verinin büyüklüğüne polinom mertebesinde bağımlı sürede çalışacak bir algoritmayla bulabiliyorsak, bu soruya cevap olarak üretilmiş bir tahminin doğruluğunu da verinin büyüklüğüne polinom mertebesinde bağımlı sürede çalışacak bir algoritmayla kontrol edebiliriz. Bunun için verilen sorunun cevabını verecek algoritmayı çalıştırıp, onun verdiği cevabı kendi tahminimizle karşılaştırmak yeterlidir. "P=NP?" problemi bunun tersinin de doğru olup olmadığını sorar. Yani NP kategorisinde olup da P kategorisinde olmayan problemler var mıdır? Veya diğer bir dille asal çarpanların bulunması için polinom mertebesinde bir sürede çalışacak bir algoritma gerçekten yok mu yoksa var da biz mi bulamıyoruz? Bu alanın uzmanlarının çoğunun görüşü bu tür algoritmaların gerçekten de var olmadıkları için bulunamadığı (yani P nin NP'ye eşit olmadığı) şeklinde ancak bu soruya kesin bir cevap verilebilmesi şimdilik çok zor gözüküyor.
12. Aritmetiğin Temel Teoremi
Her doğal sayının sonlu sayıda asal sayının kuvvetlerinin çarpımı olarak yazılabileceğini ifade eden teorem. İspatını ilk olarak Öklid yapmıştır.
Kanıtı
Bu teorem'in ispatı, teoremin gerçek olmadığını varsayıp bunun bir çelişkiye yol açacağını göstererek yapılmıştır. Diyelim ki "n" bu teorimi çürütecek olan en küçük doğal sayı olsun. Asal olmadığına göre, n=ab şeklinde yazılabilir ve a ve b n ile 1 arasında birer doğal sayı'dır. Fakat n bu teorimi çürütecek en küçük sayı olduğundan, a ve b birer asal sayının çarpımı olarak yazılabilir. Ancak bu durumda, n de asal sayıların çarpımıdır, ve bu yüzden ilk varsayım gerçek olamaz. Bu n'in varolamayacağını gösterir ve teorimimizi ispatlar.
13. Bolzano-Weierstrass Teoremi
Bolzano-Weierstrass teoremi klasik matematik analizin temel teoremlerinden biridir. İlk kez "Fonksiyonlar" adlı kitabında Bernhard Bolzano tarafından kullanıldı. Sonraki yıllarda bu teoremin ispatı tam olarak Karl Weierstrass tarafından verilmiştir. Bu nedenle, bu teorem analizde Bolzano-Weierstrass teoremi olarak bilinir.
 , reel sayılar kümesinin, sınırlı ve sonsuz elemana sahip her alt kümesinin en az bir yığılma noktası vardır.
, reel sayılar kümesinin, sınırlı ve sonsuz elemana sahip her alt kümesinin en az bir yığılma noktası vardır.ispat:
reel sayılarda sınırlı ve sonsuz elemanlı bir küme A olsun. Reel sayılar tamlık aksiyomunu sağladığından A kümesinin supremum ve infimum'u vardır. infA=x, supA=y olsun. Bu durumda her aЄA için x≤a≤y elde edilir. [x,y] aralığını iki kapalı aralığa bölelim. Bu aralıklardan en az bir tanesi sonsuz eleman kapsar. Böylece devam edilerek tümevarımla artan(xn) ve azalan , xn<yn dizilerini oluştururuz. [xn,yn] aralığının uzunluğu yn-xn=y-x/2n ve A∩[xn,yn] kümesinin sonsuz çoklukta elemanı vardır. (xn) artan sınırlı, azalan sınırlı dizi olduklarından yakınsar. limnxn=supnxn=p ve limnyn=infnyn=q olsun. yn-xn=y-x/2n olduğundan supnxn=infnyn=p olur. ε>0 verilsin. y-x<y-x/2n olacak biçimde nЄN seçelim. bu durumda yn-p≤yn-xn<ε ve p-xn≤yn-xn<ε elde edilir. (p-ε,p+ε)aralığı A∩[xn,yn] kümesinin sonsuz çoklukta elemanını kapsadığından p noktası A kümesinin bir yığılma noktasıdır.
14. Ceva Teoremi
Ceva Teoremi, Bir ABC üçgeninde D, E ve F sırasıyla BC, CA ve AB doğru parçaları üzerindeki noktalar olmak kaydı ile AD, BE ve CF doğru parçalarının aynı noktada kesişmeleri için gerek ve yeter koşul şöyle yazılabilir:
BD.CE.AF = DE.EA.FB
Bu durum söz konusu olan doğru parçaları kenarortay, açıortay veya yükseklik olduğunda da geçerlidir.
15. Fermat'ın Küçük Teoremi
Fermat'ın küçük teoremi p asal sayı ise ve obeb(p,a)=1 yani a ve p aralarında asal ise

olduğunu belirten teoremdir.
Teorem asallık testlerinde ve bilgisayarda büyük sayılarla işlemlerde kullanılır.
16. Thales teoremi

Thales Teoremi: AC çap ise, B dik açıdır
16-Thales Teoremi, birbirine benzer iki çokgen arasında kurulmuş bağıntıdır. Geometrinin gelişmesine katkıda bulunmuştur. Hatta trigonometri ile hesaplanmış ama ispatlanmamış bazı özel durumların ispatındada Thales Teoremi kullanılmıştır.
Quo vadis?

 Önemli Matematik Kuramları
Önemli Matematik Kuramları
