Ziyaretçi
Cauchy Dağılımı
Olasılık kuramı ve istatistik bilim dallarında Cauchy-Lorentz dağılımı bir sürekli olasılık dağılımı olup, bu dağılımı ilk ortaya atan Augustin Cauchy ve Hendrik Lorentz anısına adlandırılmıştır. Matematik istatistikçiler genel olarak Cauchy dağılımı adını tercih edip kullanmaktadırlar; ama fizikçiler arasında Lorentz dağılımı veya bir Lorentz(yen) fonksiyonveya Breit-Wigner dağılımı olarak bilinip kullanılmaktadır. Fizik biliminde Cauchy-Lorentz dağılımının onemle kullanıldığı alanların bazıları şöyle anılabilir: Zorlanan rezonans fenomenini açıklayan deferensiyel eşitliğine çözüm sağlaması; spektroskopi alanında bir doğruşekil ile ayırım gösteren frekans aralığında aynı şekilde tüm atomlar birbirleriyle karşılıklı etkilemekteyken homojen genişlemeye tabi olamaları sonucu ortaya çıkan spektral doğrularının şeklinin tanımlanması; ve birçok mekanizmanın (özellikle çarpışmadan genişlemede) homojen genişleme göstermesinin açıklanması.
Karakterizasyon
Olasılık yoğunluk fonksiyonu
Cauchy dağılımı için olasılık yoğunluk fonksiyonu şudur:

Burada x0 dağılımın doruğunu tanımlayan konum parametresi ve γ ise yarı-maksimumda yarı-genişliği tanımlayan ölçek parametresidir.
Lorentziyen fonksiyonun genliği şöyle verilir:

Fizikte üç parametreli Lorentziyen fonksiyon çok kere şu türde verilir:
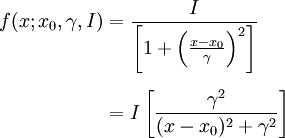
Burada I doruktaki yüksekliktir.
x0 = 0 ve γ = 1 olduğu zamanki özel hale standart Cauchy dağılımı adı verilir ve bunun olasılık yoğunluk fonksiyonu şöyle ifade edilir:

Yığmalı dağılım fonksiyonu
Yığmalı dağılım fonksiyonu şudur:

Cauchy dağılımı için ters yığmalı dağılım fonksiyonu şu olur:

Özellikleri
Cauchy dağılımı, tanımlanan hiçbir ortalaması, varyansı veya daha yüksek derecede momenti olmayan bir dağılıma örnektir. Mod değeri ve medyan değeri çok kesinlikle tanımlanmıştır ve her ikisi de x0a eşittirler.
Eğer U ve V iki tane bağımsız 0 beklenen değerli ve 1e eşit varyanslı normal dağılım gösteren rassal değişkenlerse, U/V oranı standart Cauchy dağılımı gösterir.
Eğer X1, …, Xn her biri bir standart Cauchy dağılımı gösteren bağımsız ama aynı dağılımlı rassal değişkenlerse, örneklem aritmetik ortalaması yani
(X1 + … + Xn)/n ifadesi de aynı dağılımı gösterir (Uçsal değerlerden etkilenmeyen örneklem medyani merkezsel konum ölçüsü olarak kullanılır.) Bunun doğru olduğunu isbatlamak için örneklem ortalamasının karakteristik fonksiyonu şöyle hesaplanabilir:
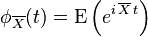
Burada örneklem ortalamasıdır. Bu örneğin göstermektedir ki merkezsel limit teoremini daha basitleştirmek için kabul edilmesi gereken sonlu varyans hipotezinin bir kenara birakilması uygun değildir . Bu sonuç, aynı zamanda Cauchy dağılımının özel bir hali olduğu Levy çarpık alfa-durağan dağılımları için de geçerli olan merkezsel limit teoreminin alışılmış olandan daha genelleştirilmiş bir şekline bir örnek sağlamaktadır.
örneklem ortalamasıdır. Bu örneğin göstermektedir ki merkezsel limit teoremini daha basitleştirmek için kabul edilmesi gereken sonlu varyans hipotezinin bir kenara birakilması uygun değildir . Bu sonuç, aynı zamanda Cauchy dağılımının özel bir hali olduğu Levy çarpık alfa-durağan dağılımları için de geçerli olan merkezsel limit teoreminin alışılmış olandan daha genelleştirilmiş bir şekline bir örnek sağlamaktadır.
Cauchy dağılımı bir sonsuza kadar bölünebilir olasılık dağılıma örnektir. Ayrıca kesinlikle dengelilik gösteren bir dağılımdir.
Standart Cauchy dağılımı 1 serbestlik derecesi bulunan Student'in t-dağılımı ile aynidir.
Cauchy dağılımının ait olduğu konum-ölçek ailesi tipte dağılımlara lineer kesirsel dönüşümler altında kapalı olma karekterini taşırlar.
Karakteristik fonksiyon
X Cauchy dağılım gösteren bir rassal değişken olsun. Cauchy dağılımı için karakteristik fonksiyon şöyle verilir:

Neden ortalama tanımlanmaz?
Eger bir olasılık dağılımı f(x) ile ifade edilen bir olasilik yogunluk fonksiyonu] gosteriyorsa, ortalama veya beklenen değeri sudur:

Burada sorun bunun su ifade ile ayni olup olmadigidir:
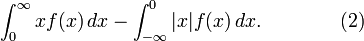
Verilen (2) ifadesinin en çok bir terimi sonsuz ise bu iki ifade birbirine aynıdır. Fakat Cauchy dağılımı halinde (2) ifadesi için (sırayla pozitif ve negatif olan) her iki terim de sonsuzdur. Bu demektir ki (2) tanımlanamamaktadır. Ayrıca eğer (1) bir Lebesque entegrali olarak kabul edilirse, bu halde (1) de tanımlanamamaktdır; çünkü o zaman (1) ifadesinin (")nin pozitif ve negatif terimleri arasındaki fark olduğu görülür. Buna karşılık (1) ifadesi bir bir Lebesque entegrali olacak yerde bir has olmayan entegral olarak kabul edilirse, o halde (1)'in mutlaka her zaman iyi-tanımlanma karekteri bulunmayacaktır ama zaten (2) tanımlanamaktadır. O zaman (1) ifadesi şöyle yazilabilir:

ve bu sıfıra eşit olan Cauchy ana değeridir. Fakat (1) ifadesi değişik şekilde şöyle de yazılabilir:

Bu integral hesaplanınca açıkca görülür ki bu sıfır değerde değildir.
Beklenen değer için olasılık kuramında ortaya çıkarılan çeşitli sonuçlar (örneğin güçlü büyük sayılar yasası), beklenen değeri bulunmayan Cauchy dağılımı için uygun olmamaktadır.
Neden ikinci moment sonsuzdur?
Ortalama anlamsiz oldugu icin bir standart Cauchy dagilimi icin varyans veya [standart sapma]] kavramlari da anlamsizdir. Ancak ortalam etrafinda ikinic momentin ele alinmasi imkân dahilindedir. Su ifadeye gore

gorulmektededir ki Cauchy dagilim icin ortalama etrafindaki ikinci moment sonsuzdur.
İlişkili dağılımlar
Nukleer fizikte ve parçacık fiziğinde, bir rezonansin enerji profili relativistik Breit-Wigner dağılımı ile belirtilir.
Sponsorlu Bağlantılar
Karakterizasyon
Olasılık yoğunluk fonksiyonu
Cauchy dağılımı için olasılık yoğunluk fonksiyonu şudur:

Burada x0 dağılımın doruğunu tanımlayan konum parametresi ve γ ise yarı-maksimumda yarı-genişliği tanımlayan ölçek parametresidir.
Lorentziyen fonksiyonun genliği şöyle verilir:

Fizikte üç parametreli Lorentziyen fonksiyon çok kere şu türde verilir:
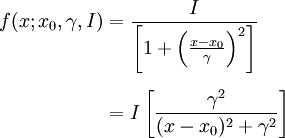
Burada I doruktaki yüksekliktir.
x0 = 0 ve γ = 1 olduğu zamanki özel hale standart Cauchy dağılımı adı verilir ve bunun olasılık yoğunluk fonksiyonu şöyle ifade edilir:

Yığmalı dağılım fonksiyonu
Yığmalı dağılım fonksiyonu şudur:

Cauchy dağılımı için ters yığmalı dağılım fonksiyonu şu olur:

Özellikleri
Cauchy dağılımı, tanımlanan hiçbir ortalaması, varyansı veya daha yüksek derecede momenti olmayan bir dağılıma örnektir. Mod değeri ve medyan değeri çok kesinlikle tanımlanmıştır ve her ikisi de x0a eşittirler.
Eğer U ve V iki tane bağımsız 0 beklenen değerli ve 1e eşit varyanslı normal dağılım gösteren rassal değişkenlerse, U/V oranı standart Cauchy dağılımı gösterir.
Eğer X1, …, Xn her biri bir standart Cauchy dağılımı gösteren bağımsız ama aynı dağılımlı rassal değişkenlerse, örneklem aritmetik ortalaması yani
(X1 + … + Xn)/n ifadesi de aynı dağılımı gösterir (Uçsal değerlerden etkilenmeyen örneklem medyani merkezsel konum ölçüsü olarak kullanılır.) Bunun doğru olduğunu isbatlamak için örneklem ortalamasının karakteristik fonksiyonu şöyle hesaplanabilir:
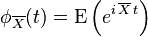
Burada
 örneklem ortalamasıdır. Bu örneğin göstermektedir ki merkezsel limit teoremini daha basitleştirmek için kabul edilmesi gereken sonlu varyans hipotezinin bir kenara birakilması uygun değildir . Bu sonuç, aynı zamanda Cauchy dağılımının özel bir hali olduğu Levy çarpık alfa-durağan dağılımları için de geçerli olan merkezsel limit teoreminin alışılmış olandan daha genelleştirilmiş bir şekline bir örnek sağlamaktadır.
örneklem ortalamasıdır. Bu örneğin göstermektedir ki merkezsel limit teoremini daha basitleştirmek için kabul edilmesi gereken sonlu varyans hipotezinin bir kenara birakilması uygun değildir . Bu sonuç, aynı zamanda Cauchy dağılımının özel bir hali olduğu Levy çarpık alfa-durağan dağılımları için de geçerli olan merkezsel limit teoreminin alışılmış olandan daha genelleştirilmiş bir şekline bir örnek sağlamaktadır.Cauchy dağılımı bir sonsuza kadar bölünebilir olasılık dağılıma örnektir. Ayrıca kesinlikle dengelilik gösteren bir dağılımdir.
Standart Cauchy dağılımı 1 serbestlik derecesi bulunan Student'in t-dağılımı ile aynidir.
Cauchy dağılımının ait olduğu konum-ölçek ailesi tipte dağılımlara lineer kesirsel dönüşümler altında kapalı olma karekterini taşırlar.
Karakteristik fonksiyon
X Cauchy dağılım gösteren bir rassal değişken olsun. Cauchy dağılımı için karakteristik fonksiyon şöyle verilir:

Neden ortalama tanımlanmaz?
Eger bir olasılık dağılımı f(x) ile ifade edilen bir olasilik yogunluk fonksiyonu] gosteriyorsa, ortalama veya beklenen değeri sudur:

Burada sorun bunun su ifade ile ayni olup olmadigidir:
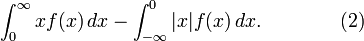
Verilen (2) ifadesinin en çok bir terimi sonsuz ise bu iki ifade birbirine aynıdır. Fakat Cauchy dağılımı halinde (2) ifadesi için (sırayla pozitif ve negatif olan) her iki terim de sonsuzdur. Bu demektir ki (2) tanımlanamamaktadır. Ayrıca eğer (1) bir Lebesque entegrali olarak kabul edilirse, bu halde (1) de tanımlanamamaktdır; çünkü o zaman (1) ifadesinin (")nin pozitif ve negatif terimleri arasındaki fark olduğu görülür. Buna karşılık (1) ifadesi bir bir Lebesque entegrali olacak yerde bir has olmayan entegral olarak kabul edilirse, o halde (1)'in mutlaka her zaman iyi-tanımlanma karekteri bulunmayacaktır ama zaten (2) tanımlanamaktadır. O zaman (1) ifadesi şöyle yazilabilir:

ve bu sıfıra eşit olan Cauchy ana değeridir. Fakat (1) ifadesi değişik şekilde şöyle de yazılabilir:

Bu integral hesaplanınca açıkca görülür ki bu sıfır değerde değildir.
Beklenen değer için olasılık kuramında ortaya çıkarılan çeşitli sonuçlar (örneğin güçlü büyük sayılar yasası), beklenen değeri bulunmayan Cauchy dağılımı için uygun olmamaktadır.
Neden ikinci moment sonsuzdur?
Ortalama anlamsiz oldugu icin bir standart Cauchy dagilimi icin varyans veya [standart sapma]] kavramlari da anlamsizdir. Ancak ortalam etrafinda ikinic momentin ele alinmasi imkân dahilindedir. Su ifadeye gore

gorulmektededir ki Cauchy dagilim icin ortalama etrafindaki ikinci moment sonsuzdur.
İlişkili dağılımlar
- İki bağımsız standart normal dağılım gösteren rassal değişşkenin birbirine oranı bir standart Cauchy dağılımı gösterir. Cauchy dağılımının bir oran dağılımı olduğu böylece açığa çıkar.
- Standart Cauchy dağılımı, yani Cauchy(0,1) 1 serbestlik derecesi gösteren Student'in t dağılımına eşit olup Student'in t-dağılımınınn bir özel halidir.
- Levy çarpık alfa-durağan dağılım ile ilişki şöyle verilir: Eğer X˜Levy − SαS(1,0,γ,μ) ise, o halde X˜Cauchy(μ,γ). olur.
Nukleer fizikte ve parçacık fiziğinde, bir rezonansin enerji profili relativistik Breit-Wigner dağılımı ile belirtilir.
Olasılık yoğunluk fonksiyonu

Yeşil çizgi standart Cauchy fonksiyonunu gösterir.
Yığmalı dağılım fonksiyonu
Renkler yukarıdaki olasılık yoğunluk fonksiyonu eğrilerinin aynıdır

Yeşil çizgi standart Cauchy fonksiyonunu gösterir.
Yığmalı dağılım fonksiyonu
Renkler yukarıdaki olasılık yoğunluk fonksiyonu eğrilerinin aynıdır

 Cauchy Dağılımı
Cauchy Dağılımı

