Ziyaretçi
Üstel Dağılım
Olasılık kuramı ve istatistik bilim dallarında üstel dağılımı bir sürekli olasılık dağılımları grubudur. Sabit ortalama değişme haddinde ortaya çıkan bağımsız olaylar arasındaki zaman aralığını modelleştirirken bir üstel dağılım doğal olarak ortaya çıkar.
Tipik karakteristikler
Olasılık yoğunluk fonksiyonu
Bir üstel dağılım için olasılık yoğunluk fonksiyonu şu şekli alır:
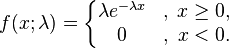
Burada λ > 0 dağılım için tek parametredir ve çok zaman oran parametresi olarak anılır. Dağılım için destek [0,∞) aralığında verilir. Eğer X rassal değişkeni bu üstel dağılım gösteriyorsa bu şöyle yazılır:
X ~ Üstel(λ). Ancak bir diğer şekilde değişik parametreleme ile ise üstel dağılım için olasılık yoğunluk fonksiyonu şöyle ifade edilir:
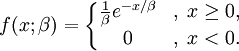
Burada β > 0 bir ölçek parametresidir ve yukarıda tanımlanan oran parametresi olan λ'nın bir üstü değeri çarpım tersi, yani β=1/λ; dır. Bu çeşit tanımlamada β kalım parametresi çünkü eğer bir rassal değişken X bir biyolojik veya mekanik sistem M için ömür geçirme zaman uzunluğu ise ve X ~ Üstel(β) ise

yani M için beklenen hayatta kalım süresi zaman birimleri ile β olur.
Bu ikinci şekilde tanımlama bazan birinci tanımlamadan daha kullanışlı olur ve bazı istatistikçiler bu ikinci tanımı üstel dağılım için standard tanım kabul etmektedirler.
Bu gerçek dikkat çekilmesi gereken bir konu olarak burada işaret edilmektedir. Çünkü iki değişik tanım bazan bir kavram karmaşaklığına neden olmaktadır. Genel olarak üstel dağılımı kullanan istatistikçi birinci tanım kullanırsa
X ~ Üstel(λ) ve ikinci tanımı kullanırsa
X ~ Üstel(β) yazılır ve β=1/λ olur.
Yığmalı dağılım fonksiyonu
Genel olarak kullanılan bir yönteme göre yığmalı dağılım fonksiyonu şu ifade ile verilir:
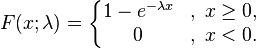
Ortaya çıkma ve uygulanma
Bir homojen Poisson süreçde varışlar arasındaki zaman dönemlerini tanımlarken üstel dağılım doğal olarak ortaya çıkar.
Üstel dağılım geometrik dağılımin sürekli dağılımlara uzantısı olarak görülebilir. Geometrik dağılım durumu değiştirmek gereken Bernoulli süreçlerinin sayısını tanımlar ve bu yüzden bir ayrık süreçtir. Buna karşılık, durumu değiştirmek için sürekli bir süreç için geçen zamanı tanımlar.
Pratik gerçek hayatta bir değişme oranının (veya her zaman birimi içinde olasılığın) gerçekleşmesi çok nadirdir. Örneğin, bir mobil telefona gelen çağrılar birim saatin gün içindeki yerine değişir. Fakat araştırmamızı günün öyle bir zaman aralığına odaklayabiliriz ki (diyelim öğleden sonra 2 ile 4), bu zaman aralığından gelen telefon çağrı ortalamları kabaca sabit olabilir. Üstel dağılım o halde iyi bir yaklaşık model olarak kullanılabilir ve en son çağrıdan sonra ne zaman aralığından sonra bir yeni çağrının geleceği hakkında üstel dağılım kullanarak tahmin yapabiliriz.
Benzer şekilde uzun ve karmaşık varsayımlar ve açıklamalar pratikte yaklaşık olarak üstel dağılım gösteren değişkenlere da uygulan şu olaylar için de uygulanabilir:
Özellikler
Ortalama ve varyans
Bir λ oran parametresi ile üstel dağılım gösteren bir X rassal değişkeni için ortalama veya beklenen değer şöyle verilir:
 Bu verilen pratik örneklerden sağduyu ile çıkarılabilir. Örneğin eğer telefon çağrı ortalama oranı saatte 3 ise (λ), her telefon çağrısı için ortalama 1/3 saat veya 20 dakika (β) beklemek gerekmektedir
Bu verilen pratik örneklerden sağduyu ile çıkarılabilir. Örneğin eğer telefon çağrı ortalama oranı saatte 3 ise (λ), her telefon çağrısı için ortalama 1/3 saat veya 20 dakika (β) beklemek gerekmektedir
X icin varyans şöyle verilir

Belleksizlik
Üstel dağılımın bir önemli niteliği de belleksiz olmasıdır. Bu demektir ki eğer bir rassal değişken T üstel dağılım gösteriyorsa, onun koşullu olasılığı

ifadesine uygunluk gösterir. Buna göre, bir hizmet noktasındaki hizmet ve bekleme kuyruğu problemi örneği için bir koşullu olasılık olan ilk varışın 30 saniye geçtikten sonra ortaya çıkmadığını bilerek ilk varıştan sonra 10 saniyeden daha fazla beklemek gereğinin olasılığının, birinci varıştan sonra 10 saniyeden daha fazla bekleme gereğinin koşulsuz başlangıç olasığı arasında bir fark yoktur. Bu çok kere olasılık hesaplarını ilk gören kişiler tarafından yanlış anlaşılmaktadır:
P(T > 40 | T > 30) = P(T > 10) gerçeği
T>40 ve T>30 olayları birbirinden [bağımsız]]dır anlamına gelmez. İlk varışa kadar T bekleme zamanının olasılık dağılımının belleksizlik karakteri olduğunu bildirmek

olur demektir; yoksa
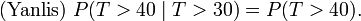
demek değildir çünkü bu ikinci ifade bağımsızlık kavramını açıklar ve burada olaylar bağımsız değildir.
Bütün mevcut dağılımlar arasında sadece üstel dağılımlar ve geometrik dağılımlar belleksizlik özelliği taşırlar.
Üstel dağılımının ayrıca sabit bir tehlike fonksiyonu bulunmaktadır.
Dörtebirlikler
Bir λ parametreli üstel dağılım için (ters yığmalı dağılım fonksiyonu) şudur:
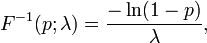
burada 0 ≤ p < 1.
Onun için şu ifadeler dörttebirlikler verir:
birinci dörttebirlik :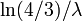 medyan :
medyan :  üçüncü dörttebirlik :
üçüncü dörttebirlik : 
Kullback-Leibler ayrılımı
'Gerçek' üstel dağılım olan Exp(λ0) ile ('yaklaşık' dağılım) olan Exp(λ) arasında yönlendirilmiş Kullback-Leibler ayrılımı şöyle verilir:

Maksimum entropi dağılımı
[0,∞) and mean μ, de destekli bulunan bütün sürekli olasılık dağılımları arasında sadece λ = 1/μ parametresi ile üstel dağılımın en yüksek entropisi bulunmaktadır.
Üstel rassal değişirlerin minimumu için dağılım
X1, ..., Xn bağımsız oran parametreleri λ1, ..., λn olan üstel olarak dağılım gösteren rassal değişkenler olsun. Bu halde
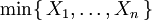
ifadesi de üstel dağılımdır ve bu dağılımın parametresi

olur.
Fakat,
 üstel dağılım göstermez.
üstel dağılım göstermez.
Parametre tahmin edilmesi
Verilmiş bir değişkenin üstel dağılım gösterdiği bilinmiş olsun ve oran parametresi olan λnın değerinin tahmin edilmesi gerekmektedir.
Maksimum olabilirlilik
İlgi gösterilen değişkenden bir bağımsız aynen dağılma gösteren örneklem x = (x1, ..., xn) olarak seçilsin; o halde λ için olabilirlilik fonksiyonu şöyle verilir:

burada

örnek ortalamasıdır.
Olabilirlik fonksiyonunun logaritmasının türevi şudur:

Bu nedenle oran parametresinin maksimum olabilirlilik tahmini şöyle verilir:

Bayes tipi sonuç çıkartıcı analiz
Bir üstel dağılımın eşlenik önseli bir gamma dağılımı olur (çünkü üstel dağılım bir özel hal gamma dağılımıdır). Gamma olasılık dağılım fonksiyonunun şu çeşit parametrik tanımı analizde kullanılacaktır:

Bu halde p için sonsal dağılım yukarıda tanımlanan olabilirlilik fonksiyonu ve bir gamma önsel ile şöyle ifade edilebilir:

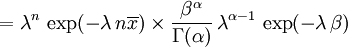

Şimdi p için sonsal yoğunluk bir kayıp olmuş normalizasyon sabiti değerine kadar tanımlanmıştır.
Bunun dağılımı gamma olduğu için bu eksiklik hemen tamamlanabilir ve şu ifade elde edilir:
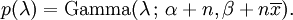
Burada parametre α önsel gözlemlerin sayısı olarak yorumlanabilir ve β önsel gözlemlerin toplamıdır.
Üstel değişebilirleri üretme
Üstel değişebilirler için üstel dağılım üreten kavramsal olarak bir basit yöntem ters dönüşüm örnekleme dayanır: Verilmiş olan bir birim aralıkta, yani [0,1] arasında, bulunan bir tekdüze dağılımdan çekilmiş U rassal değişebiliri verilmiş olsun,

değişebiliri bir üstel dağılım gösterir ve F − 1 ifadesi

ile tanımlanmış bir [kuantil fonksiyonu]] olur.
Bunun yanında, eğer U (0;1) aralığında bir tekdüze dağılım gösterirse, 1 − U için de aynı özellik gerçektir. Bu demektir ki şu şekilde üstel değişebilirler üretilebilir:

Üstel değişebilirlerin diğer yöntemlerle üretilebilmesi Knuth (1998)de ve Luc Devroye (1986) da görülebilir.
Üstel değişebilirleri üretmek için bir hızlı yöntem [[zigurat algoritması] iledir.
İlişkili dağılımlar
 ve
ve  ise
ise

olur yani Y Weibull dağılım gösterir. Özellikle, her üstel dağılım da bir Weibull dağılımıdır.
 ve
ve  . ise
. ise
 olur; yani Y bir Rayleigh dağılımı gösterir.
olur; yani Y bir Rayleigh dağılımı gösterir.
 ve
ve  . ise
. ise
 , olur yani Y Gumbel dağılımı gösterir.
, olur yani Y Gumbel dağılımı gösterir.
 olur yani Y Laplace dağılımı gösterir.
olur yani Y Laplace dağılımı gösterir.
 ise
ise
 olur; yani Y bir üstel dağılım gösterir.
olur; yani Y bir üstel dağılım gösterir.
 and
and  ise
ise
 , olur yani Y tekdüze dağılım gösterir.
, olur yani Y tekdüze dağılım gösterir.
 . ise
. ise 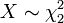 olur yani X icin 2 serbestlik derecesi olan ki-kare dağılımı geçerlidir.
olur yani X icin 2 serbestlik derecesi olan ki-kare dağılımı geçerlidir.
Sponsorlu Bağlantılar
Tipik karakteristikler
Olasılık yoğunluk fonksiyonu
Bir üstel dağılım için olasılık yoğunluk fonksiyonu şu şekli alır:
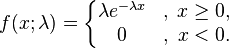
Burada λ > 0 dağılım için tek parametredir ve çok zaman oran parametresi olarak anılır. Dağılım için destek [0,∞) aralığında verilir. Eğer X rassal değişkeni bu üstel dağılım gösteriyorsa bu şöyle yazılır:
X ~ Üstel(λ). Ancak bir diğer şekilde değişik parametreleme ile ise üstel dağılım için olasılık yoğunluk fonksiyonu şöyle ifade edilir:
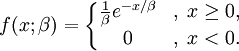
Burada β > 0 bir ölçek parametresidir ve yukarıda tanımlanan oran parametresi olan λ'nın bir üstü değeri çarpım tersi, yani β=1/λ; dır. Bu çeşit tanımlamada β kalım parametresi çünkü eğer bir rassal değişken X bir biyolojik veya mekanik sistem M için ömür geçirme zaman uzunluğu ise ve X ~ Üstel(β) ise

yani M için beklenen hayatta kalım süresi zaman birimleri ile β olur.
Bu ikinci şekilde tanımlama bazan birinci tanımlamadan daha kullanışlı olur ve bazı istatistikçiler bu ikinci tanımı üstel dağılım için standard tanım kabul etmektedirler.
Bu gerçek dikkat çekilmesi gereken bir konu olarak burada işaret edilmektedir. Çünkü iki değişik tanım bazan bir kavram karmaşaklığına neden olmaktadır. Genel olarak üstel dağılımı kullanan istatistikçi birinci tanım kullanırsa
X ~ Üstel(λ) ve ikinci tanımı kullanırsa
X ~ Üstel(β) yazılır ve β=1/λ olur.
Yığmalı dağılım fonksiyonu
Genel olarak kullanılan bir yönteme göre yığmalı dağılım fonksiyonu şu ifade ile verilir:
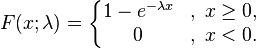
Ortaya çıkma ve uygulanma
Bir homojen Poisson süreçde varışlar arasındaki zaman dönemlerini tanımlarken üstel dağılım doğal olarak ortaya çıkar.
Üstel dağılım geometrik dağılımin sürekli dağılımlara uzantısı olarak görülebilir. Geometrik dağılım durumu değiştirmek gereken Bernoulli süreçlerinin sayısını tanımlar ve bu yüzden bir ayrık süreçtir. Buna karşılık, durumu değiştirmek için sürekli bir süreç için geçen zamanı tanımlar.
Pratik gerçek hayatta bir değişme oranının (veya her zaman birimi içinde olasılığın) gerçekleşmesi çok nadirdir. Örneğin, bir mobil telefona gelen çağrılar birim saatin gün içindeki yerine değişir. Fakat araştırmamızı günün öyle bir zaman aralığına odaklayabiliriz ki (diyelim öğleden sonra 2 ile 4), bu zaman aralığından gelen telefon çağrı ortalamları kabaca sabit olabilir. Üstel dağılım o halde iyi bir yaklaşık model olarak kullanılabilir ve en son çağrıdan sonra ne zaman aralığından sonra bir yeni çağrının geleceği hakkında üstel dağılım kullanarak tahmin yapabiliriz.
Benzer şekilde uzun ve karmaşık varsayımlar ve açıklamalar pratikte yaklaşık olarak üstel dağılım gösteren değişkenlere da uygulan şu olaylar için de uygulanabilir:
- bir radyoaktif parçacığın bozunmasına kadar geçen zaman veya bir geiger sayacının birbirini takibedecek düdük seslerinin arasında geçen zamanın tahmini;
- gelecek telefon çağrısını en son yaptığınız çağrıdan ne kadar zaman sonra yapacağınız;
- indirgenmis şekilde olan kredi rizikosu modelinde bir firmanın borçluları ile ilgili olarak en son borcunu ödeyemiyecegini bildiren borçludan ne zaman sonra bir başka daha borç ödeyemiyecek borçlu çıkacağını tahmin etmek.
Özellikler
Ortalama ve varyans
Bir λ oran parametresi ile üstel dağılım gösteren bir X rassal değişkeni için ortalama veya beklenen değer şöyle verilir:
 Bu verilen pratik örneklerden sağduyu ile çıkarılabilir. Örneğin eğer telefon çağrı ortalama oranı saatte 3 ise (λ), her telefon çağrısı için ortalama 1/3 saat veya 20 dakika (β) beklemek gerekmektedir
Bu verilen pratik örneklerden sağduyu ile çıkarılabilir. Örneğin eğer telefon çağrı ortalama oranı saatte 3 ise (λ), her telefon çağrısı için ortalama 1/3 saat veya 20 dakika (β) beklemek gerekmektedirX icin varyans şöyle verilir

Belleksizlik
Üstel dağılımın bir önemli niteliği de belleksiz olmasıdır. Bu demektir ki eğer bir rassal değişken T üstel dağılım gösteriyorsa, onun koşullu olasılığı

ifadesine uygunluk gösterir. Buna göre, bir hizmet noktasındaki hizmet ve bekleme kuyruğu problemi örneği için bir koşullu olasılık olan ilk varışın 30 saniye geçtikten sonra ortaya çıkmadığını bilerek ilk varıştan sonra 10 saniyeden daha fazla beklemek gereğinin olasılığının, birinci varıştan sonra 10 saniyeden daha fazla bekleme gereğinin koşulsuz başlangıç olasığı arasında bir fark yoktur. Bu çok kere olasılık hesaplarını ilk gören kişiler tarafından yanlış anlaşılmaktadır:
P(T > 40 | T > 30) = P(T > 10) gerçeği
T>40 ve T>30 olayları birbirinden [bağımsız]]dır anlamına gelmez. İlk varışa kadar T bekleme zamanının olasılık dağılımının belleksizlik karakteri olduğunu bildirmek

olur demektir; yoksa
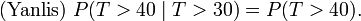
demek değildir çünkü bu ikinci ifade bağımsızlık kavramını açıklar ve burada olaylar bağımsız değildir.
Bütün mevcut dağılımlar arasında sadece üstel dağılımlar ve geometrik dağılımlar belleksizlik özelliği taşırlar.
Üstel dağılımının ayrıca sabit bir tehlike fonksiyonu bulunmaktadır.
Dörtebirlikler
Bir λ parametreli üstel dağılım için (ters yığmalı dağılım fonksiyonu) şudur:
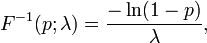
burada 0 ≤ p < 1.
Onun için şu ifadeler dörttebirlikler verir:
birinci dörttebirlik :
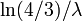 medyan :
medyan :  üçüncü dörttebirlik :
üçüncü dörttebirlik : 
Kullback-Leibler ayrılımı
'Gerçek' üstel dağılım olan Exp(λ0) ile ('yaklaşık' dağılım) olan Exp(λ) arasında yönlendirilmiş Kullback-Leibler ayrılımı şöyle verilir:

Maksimum entropi dağılımı
[0,∞) and mean μ, de destekli bulunan bütün sürekli olasılık dağılımları arasında sadece λ = 1/μ parametresi ile üstel dağılımın en yüksek entropisi bulunmaktadır.
Üstel rassal değişirlerin minimumu için dağılım
X1, ..., Xn bağımsız oran parametreleri λ1, ..., λn olan üstel olarak dağılım gösteren rassal değişkenler olsun. Bu halde
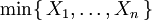
ifadesi de üstel dağılımdır ve bu dağılımın parametresi

olur.
Fakat,
 üstel dağılım göstermez.
üstel dağılım göstermez.Parametre tahmin edilmesi
Verilmiş bir değişkenin üstel dağılım gösterdiği bilinmiş olsun ve oran parametresi olan λnın değerinin tahmin edilmesi gerekmektedir.
Maksimum olabilirlilik
İlgi gösterilen değişkenden bir bağımsız aynen dağılma gösteren örneklem x = (x1, ..., xn) olarak seçilsin; o halde λ için olabilirlilik fonksiyonu şöyle verilir:

burada

örnek ortalamasıdır.
Olabilirlik fonksiyonunun logaritmasının türevi şudur:

Bu nedenle oran parametresinin maksimum olabilirlilik tahmini şöyle verilir:

Bayes tipi sonuç çıkartıcı analiz
Bir üstel dağılımın eşlenik önseli bir gamma dağılımı olur (çünkü üstel dağılım bir özel hal gamma dağılımıdır). Gamma olasılık dağılım fonksiyonunun şu çeşit parametrik tanımı analizde kullanılacaktır:

Bu halde p için sonsal dağılım yukarıda tanımlanan olabilirlilik fonksiyonu ve bir gamma önsel ile şöyle ifade edilebilir:

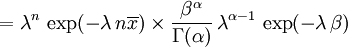

Şimdi p için sonsal yoğunluk bir kayıp olmuş normalizasyon sabiti değerine kadar tanımlanmıştır.
Bunun dağılımı gamma olduğu için bu eksiklik hemen tamamlanabilir ve şu ifade elde edilir:
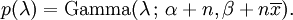
Burada parametre α önsel gözlemlerin sayısı olarak yorumlanabilir ve β önsel gözlemlerin toplamıdır.
Üstel değişebilirleri üretme
Üstel değişebilirler için üstel dağılım üreten kavramsal olarak bir basit yöntem ters dönüşüm örnekleme dayanır: Verilmiş olan bir birim aralıkta, yani [0,1] arasında, bulunan bir tekdüze dağılımdan çekilmiş U rassal değişebiliri verilmiş olsun,

değişebiliri bir üstel dağılım gösterir ve F − 1 ifadesi

ile tanımlanmış bir [kuantil fonksiyonu]] olur.
Bunun yanında, eğer U (0;1) aralığında bir tekdüze dağılım gösterirse, 1 − U için de aynı özellik gerçektir. Bu demektir ki şu şekilde üstel değişebilirler üretilebilir:

Üstel değişebilirlerin diğer yöntemlerle üretilebilmesi Knuth (1998)de ve Luc Devroye (1986) da görülebilir.
Üstel değişebilirleri üretmek için bir hızlı yöntem [[zigurat algoritması] iledir.
İlişkili dağılımlar
- Bir üstel dağılım bir gamma dağılımının bir özel halidir ve kullanılan parametre setine göre
- Hem bir üstel dağılım ve hem de bir gamma dağılım, faz-tipi dağılımın ozel halleridir.
- Eğer
 ve
ve  ise
ise
olur yani Y Weibull dağılım gösterir. Özellikle, her üstel dağılım da bir Weibull dağılımıdır.
- Eğer
 ve
ve  . ise
. ise olur; yani Y bir Rayleigh dağılımı gösterir.
olur; yani Y bir Rayleigh dağılımı gösterir.- Eğer
 ve
ve  . ise
. ise , olur yani Y Gumbel dağılımı gösterir.
, olur yani Y Gumbel dağılımı gösterir.- Eğer iki bağımsız üstel dağılımı olan
 ve
ve  için
için  ise
ise
 olur yani Y Laplace dağılımı gösterir.
olur yani Y Laplace dağılımı gösterir.- Bağımsız üstel dağılımlar olan
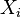 için
için
 ise
ise olur; yani Y bir üstel dağılım gösterir.
olur; yani Y bir üstel dağılım gösterir.- Eger
 and
and  ise
ise , olur yani Y tekdüze dağılım gösterir.
, olur yani Y tekdüze dağılım gösterir.- Eğer
 . ise
. ise 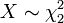 olur yani X icin 2 serbestlik derecesi olan ki-kare dağılımı geçerlidir.
olur yani X icin 2 serbestlik derecesi olan ki-kare dağılımı geçerlidir. üstel dağılımlı ve bağımsız olsun ve
üstel dağılımlı ve bağımsız olsun ve  olsun; o halde
olsun; o halde 
 ise
ise  olur
olur

 Üstel Dağılım
Üstel Dağılım


