Ziyaretçi
N-küre hacminin türevi
Vikipedi, özgür ansiklopedi
Geometri'de,bir küre'nin hacmi için bir özel durum n-boyutlu Euclid uzayı içindeki bir kürenin n-boyutlu hacmidir .
n-kürenin hacimlerinin türevleri
Genel form (özyineleme formu)
n-kürenin yarıçapı r. olmak üzere V(n)[r] , n-küre
hacmi

Çünkü bu yarıçapın iki katı uzunlukta düz bir çizgidir i.e.

n ≥ 1 için:

 kuvvetten yarıçaplı hacim
kuvvetten yarıçaplı hacim
 kuvvetten yarıçaplı n-küre'nin hacmini indüksiyon yoluyla gösterebiliriz .Tek boyutludan yararlanmak n boyutlu çıkarımlar için destek olur:
kuvvetten yarıçaplı n-küre'nin hacmini indüksiyon yoluyla gösterebiliriz .Tek boyutludan yararlanmak n boyutlu çıkarımlar için destek olur:
Buradan:




Biz şimdi bütün n ≥ 1,için kuvvetten yarıçap uzunlukluklu n-kürenin hacmini; birim kürenin hacmini n-kürenin V(n) ile gösterirsek:
kuvvetten yarıçap uzunlukluklu n-kürenin hacmini; birim kürenin hacmini n-kürenin V(n) ile gösterirsek:


İlk birkaç adım
V(2) durumunda

birim çember bölgesinden,son türevler(çıkarımlar)'la,birim küre hacmi, kolayca:

Genel Durum
Genlleştirilmiş herhangi boyutta bir türevlerini denemek için:


Görüldüğü gibi,hiperküre boyut sayısı arttıkça sıkıştıkça sıkışır.
u değişken değiştirmesi koyarak = 1 − x2 :


integral'in sağı beta fonksiyonu olarak bilinir:

gama fonksiyonu terimleri ilede gösterilebilir:

Bütün l n ≥ 1 için
 den dolayı induksiyon'la kolayca doğrulanabilir:
den dolayı induksiyon'la kolayca doğrulanabilir:

Genel form ve yüzey alanı
n-kürenin "yüzey alanı" ("n" − 1)-boyutlu (n − 1)-kürenin hacim ölçümü ,n-küre hacimli kürenin yarıçapı ile kolayca bulunabilir .
Bu nedenle n-küre yarıçapı r ile gösterirsek

Buradan "yüzey alanı"
Vikipedi, özgür ansiklopedi
Sponsorlu Bağlantılar
Geometri'de,bir küre'nin hacmi için bir özel durum n-boyutlu Euclid uzayı içindeki bir kürenin n-boyutlu hacmidir .
n-kürenin hacimlerinin türevleri
Genel form (özyineleme formu)
n-kürenin yarıçapı r. olmak üzere V(n)[r] , n-küre
hacmi

Çünkü bu yarıçapın iki katı uzunlukta düz bir çizgidir i.e.

n ≥ 1 için:

 kuvvetten yarıçaplı hacim
kuvvetten yarıçaplı hacim  kuvvetten yarıçaplı n-küre'nin hacmini indüksiyon yoluyla gösterebiliriz .Tek boyutludan yararlanmak n boyutlu çıkarımlar için destek olur:
kuvvetten yarıçaplı n-küre'nin hacmini indüksiyon yoluyla gösterebiliriz .Tek boyutludan yararlanmak n boyutlu çıkarımlar için destek olur: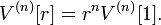
Buradan:




Biz şimdi bütün n ≥ 1,için
 kuvvetten yarıçap uzunlukluklu n-kürenin hacmini; birim kürenin hacmini n-kürenin V(n) ile gösterirsek:
kuvvetten yarıçap uzunlukluklu n-kürenin hacmini; birim kürenin hacmini n-kürenin V(n) ile gösterirsek:

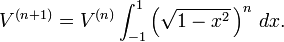
İlk birkaç adım
V(2) durumunda

birim çember bölgesinden,son türevler(çıkarımlar)'la,birim küre hacmi, kolayca:

Genel Durum
Genlleştirilmiş herhangi boyutta bir türevlerini denemek için:

Burada integrandın davranışını grafik yoluyla kolayca görselleştirebiliriz:

Görüldüğü gibi,hiperküre boyut sayısı arttıkça sıkıştıkça sıkışır.
u değişken değiştirmesi koyarak = 1 − x2 :


integral'in sağı beta fonksiyonu olarak bilinir:

gama fonksiyonu terimleri ilede gösterilebilir:

Bütün l n ≥ 1 için
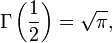 den dolayı induksiyon'la kolayca doğrulanabilir:
den dolayı induksiyon'la kolayca doğrulanabilir:
Genel form ve yüzey alanı
n-kürenin "yüzey alanı" ("n" − 1)-boyutlu (n − 1)-kürenin hacim ölçümü ,n-küre hacimli kürenin yarıçapı ile kolayca bulunabilir .
Bu nedenle n-küre yarıçapı r ile gösterirsek

Buradan "yüzey alanı"
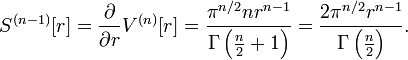

 N-Küre Hacminin Türevi
N-Küre Hacminin Türevi
