Ziyaretçi
fraktal'ı kısaca açıklar mısınız?
Fraktal
Vikipedi, özgür ansiklopedi
Vikipedi, özgür ansiklopedi
Sponsorlu Baglantilar
Fraktal parçalanmış ya da kırılmış anlamına gelen Lâtince fractus kelimesinden gelmiş bir teoremdir ve kendi kendini tekrar eden ama sonsuza kadar küçülen sekilleri, kendine benzer bir cisimde cismi oluşturan parçalar ya da bileşenler cismin bütününü inceler. İlk olarak 1975'de Polonya asıllı matematikçi Benoit Mandelbrot tarafından ortaya atıldığı varsayılır. Düzensiz ayrıntılar ya da desenler giderek küçülen ölçeklerde yinelenir ve tümüyle soyut nesnelerde sonsuza kadar sürebilir; tam tersi de her parçanın her bir parçası büyütüldüğünde, gene cismin bütününe benzemesi olayıdır
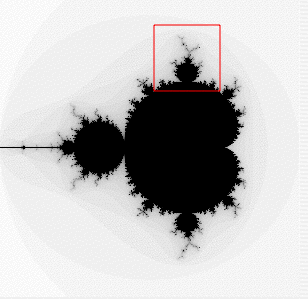
Bir fraktalı giderek yakınlaşarak izleyen bir animasyon. Simetriye dikkat ediniz.

 Fraktal nedir?
Fraktal nedir?




 <3
<3

