Arama

Fraktal Geometri

Güncelleme: 19 Kasım 2011 Gösterim: 31.707 Cevap: 3

Cevap Yaz

ThinkerBeLL

VIP VIP Üye

12 Mart 2009 Mesaj #1

VIP VIP Üye

Fraktal
Vikipedi, özgür ansiklopedi

Bir fraktalı giderek yakınlaşarak izleyen bir animasyon. Simetriye dikkat ediniz.
Sponsorlu Bağlantılar

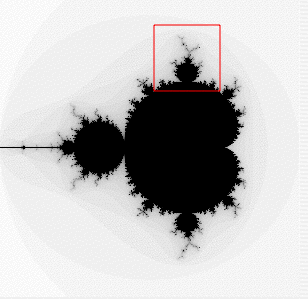
Fraktal parçalanmış ya da kırılmış anlamına gelen Lâtince fractus kelimesinden gelmiş bir teoremdir ve kendi kendini tekrar eden ama sonsuza kadar küçülen sekilleri, kendine benzer bir cisimde cismi oluşturan parçalar ya da bileşenler cismin bütününü inceler. İlk olarak 1975'de Polonya asıllı matematikçi Benoit Mandelbrot tarafından ortaya atıldığı varsayılır. Düzensiz ayrıntılar ya da desenler giderek küçülen ölçeklerde yinelenir ve tümüyle soyut nesnelerde sonsuza kadar sürebilir; tam tersi de her parçanın her bir parçası büyütüldüğünde, gene cismin bütününe benzemesi olayıdır. Doğada görebilen örnekler bazı bitkilerin yapılarıdır.

Sierpinski üçgeni; mutlak surette simetrik bir fraktal

Ad: Triangle_sierpinski_animat.gif
Gösterim: 1265
Boyut: 41.6 KB

Teoremin Gelişimi

Fraktal

Benoit Mandelbrot, IBM Laboratuvarlarında çalışmaya başladığında Oyun Teorisi, iktisat, emtia fiyatları gibi çeşitli alanlarda çalışan bir mühendisti. Bu çalışmalarını tamamladığında veri iletim hatlarındaki gürültü üzerinde çalışmaya başladı. Mühendisler, veri aktarımı sırasında oluşan gürültü karşısında çaresiz kalmışlardı. Mühendislerin bu soruna bulabildikleri en iyi çare sinyal gücünü arttırmaktan ileri gidememişti. Fakat sinyal gücünün arttırılması da tam bir çözüm sağlamamıştı. İletişim esnasında halen gürültüye bağlı hatalar oluşmaktaydı.
İletim hatlarındaki gürültü doğası gereği gelişi güzel olmasına rağmen kümeler halinde gelmekteydi. İletişim süresi boyunca hatasız periyotlar arasında hatalı periyotlar yer almaktaydı. Hatalı periyotların incelenmesi, hata paterninin sanıldığından daha karmaşık olduğunu ortaya koymuştur. Mandelbrot, bir günlük veri trafiğini birer saatlik periyotlara ayırdı. Daha sonra, hatanın gözlendiği periyotları ele alıp bu periyotlar yirmişer dakikalık parçalara böldü ve yine gördü ki, bu birer saatlik periyotların içinde de yine hatasız bölümler bulunmaktaydı. Mandelbrot, hatalı bölümler daha kısa zaman aralıklarına bölmeye devam etti. Ve sonunda hatasız periyotların halen var olduğunu gösterdi. Bu arada aykırı bir durum Mandelbrot'un dikkatini çekti: hatalı periyotların hatasız periyotlara oranı periyodun uzunluğundan bağımsız olarak neredeyse sabit kalıyordu.

Fraktal (büyütüldü)

Yukarıdaki tanıma uyan dağılım fonksiyonuna sahip bir dizi, 19. yüzyılda yaşamış olan bir matematikçinin, Georg Cantor'un anısına Cantor dizisi olarak bilinir. Cantor dizisini oluşturmak için L uzunluğunda bir doğru parçası alınır. Doğru parçasının ortadaki üçte birlik kısmı silinir. Artık L/3 uzunluğunda 2 adet doğru parçası vardır. Bu doğru parçalarının da ortadaki üçte birlik kısımları çıkarılır ve bu işlem sonsuza kadar tekrarlanırsa elde edilen yapının adı Cantor Tozudur. Bu tozun koordinatları bir Cantor dizisi oluşturur. Cantor Tozu sonsuz adet noktadan oluşur ama toplam uzunluğu sıfırdır.
Mandelbrot, yukarıdaki gürültü dağılımını kullanarak sinyal gücünün arttırılmasının gürültüye bağlı hatalardan kaçınılamayacağını göstermiştir. Yapılması gereken hataları engellemek değil, düzeltecek bir mekanizma geliştirmektir.
Mandelbrot’nun kendi kendine sorduğu şu soru, daha sonraki çalışmalarını yönlendiren temel işlev olmuştur:

"İngiltere sahil şeridinin uzunluğu nedir?"
"Bu sorunun yanıtı kullanmakta olduğunuz ölçüm aracının uzunluğuna bağlıdır."

diyordu Mandelbrot. Mesela bir metrelik bir pergelin sahil boyunca yürütüldüğünü düşünün. Bulacağınız uzunluk yaklaşık bir değer olacaktır. Zira pergel, uzunluğu bir metreden daha kısa olan girinti ve çıkıntıları atlayacaktır. Pergeli yarım metreye indirdiğinizde bulacağınız sonuç bir öncekinden daha büyük, daha doğru, ama halen yaklaşık sonuç olacaktır. Bu sefer de pergel yarım metreden daha kısa olan girinti çıkıntıları ölçemeyecektir. Pergeli daha da küçülttüğünüzde elde edeceğiniz sonuç daha büyük ama halen hatalı bir değerdir. Bu zihinsel deneyi sonsuza kadar götürdüğünüzde ilginç ortaya ilginç sonuçlar çıkar. Sahil şeridi Öklid geometrisine uygun olsa idi (örneğin çember), pergel küçüldükçe yapılacak ölçüm gerçekten de çemberin çevresine eşit olacaktı. Ama sahil şeridi Mandelbrot'un öngördüğü şekilde ise ölçek atom boyutlarına inene kadar bulunan uzunluk sürekli artmaya devam eder, ancak atom ölçeğinde sonlu bir değere gidebilir. Dikkat edilirse, Cantor Tozu'nda olduğu gibi burada da ölçü biriminden (bir anlamda gözlem boyutundan) bağımsız olarak hata halen mevcuttur.

Fraktal (bir daha büyütüldü)Fraktal (bir daha büyütüldü)

Mandelbrot'nun bir sonraki sorusu ise şu olmuştur:

"Bir iplik yumağının boyutu nedir?"

Uzaktan bakıldığında yumak bir noktadan ibarettir, yani boyutu sıfırdır. Daha yakından yapılan gözlemlerde yumak yüzeyinde düzensizlikler bulunan bir küre gibidir. Boyut sayısı üçe çıkmıştır. Daha yakından bakıldığında yumağı oluşturan tek boyutlu iplik ayrık olarak gözlemlenebilir. Tek boyutlu ipliğe büyüteçle bakıldığında iplik üç boyutlu sütunlar gibi görülür. Mikroskop altında sütunlar tek boyutlu liflere, lifler ise sonunda boyutsuz noktalara dönüşmektedir. O halde, yumağın gerçek boyutu nedir?
Mandelbrot, bir birim cinsinden ölçülemez olan cisimlerin bir pütürlülük derecesine sahip olduğunu ve bu pütürlülük derecesini ölçmenin bir yolunu bulmuştur. Mandelbrot'ya göre göre ölçek değiştiğinde düzensizlik derecesi sabit kalmaktaydı. 1975 yılında Mandelbrot pütürlülük derecesinin ismini de koymuş oldu: Fraktal boyut. Pütürlülük özelliği gösteren cisimler de fraktallar adını aldı.

Etkileri
Fraktal terimi taşıdığı felsefik anlam sayesinde ve fraktalların pschedelic biçimlere sahip olması gibi özelliklerinden dolayı diğer sanatları da etkilemiş ve özellikle müzik alanında sesin görsel yansıması, fraktal şekillerin sese dönüşümü gibi alt başlıklar altında kendine yer bulmuştur. Bu özelliklerinin yanısıra "düzendeki kaos - kaostaki düzen" sloganı ile tanımlanan fraktal kavramı özellikle rock müzik dalında kendisinden etkilenen gruplara adını vermiştir. Arjantinli progressive rock grubu "Fraktal" bu grupların en tanınanıdır. Ülkemizde de adında Arjantinli meslektaşlarıyla aynı adı taşıyan pyschedelic ve progressive rock grubu "Fraktal" faaliyetlerini sürdürmektedir.

BEĞEN Paylaş Paylaş

Tanrı varsa eğer, ruhumu kutsasın... Ruhum varsa eğer!

Cevapla

ThinkerBeLL

VIP VIP Üye

12 Mart 2009 Mesaj #2

VIP VIP Üye

Fraktal Geometri

Sponsorlu Bağlantılar

Her şey, Benoit Mandelbrot’un kafasında oluşan ve basit gibi görünen bir soru ile başladı:

İngiltere’nin kıyı uzunluğu ne kadardır?

Yanıtı bulmak için yapılabilecek ilk şey, ölçeği belli bir harita bulduktan sonra, buradan kıyı şeridinin uzunluğunu, sözgelimi bir iple ölçmek ve sonucu haritanın ölçeğiyle çarparak, kıyı uzunluğunu hesaplamak olabilir. Peki, kıyı şeridinin uzunluğu ‘gerçekte’ ne kadardır? Kıyı şeridinin uçaktan çekilmiş bir dizi fotoğrafı ile daha doğru bir ölçüm yapabilirsiniz; şüphesiz bu değer, harita üzerinde hesaplanandan biraz daha büyük çıkacaktır. Biraz daha ileri gidip, tüm kıyıyı adım adım ölçtüğünüzü düşünelim; bu durumda ne kadarlık bir uzunluk hesaplayabilirsiniz? Peki ya tüm uzunluğu milimetrik bir cetvelle ölçebildiğinizi düşünün; hatta moleküler boyulara kadar uzanan hassas bir uzunluk ölçümü yapabildiğinizi... Sonuçta, ölçümlerinizi hassaslaştırdıkça, kıyı uzunluğunun sonsuza gittiğini farkedeceksiniz. Sonlu bir kara parçasının sınırları, aslında sonsuz uzunluktadır!

Bu basit ve çarpıcı sonuç, Benoit Mandelbrot gibi bir matematikçinin elinde, ‘fraktal geometri’ dediğimiz yeni bir matematik dalının temellerinin atılmasını sağladı. Mandelbrot, tabiattaki biçimlerin matematiğini keşfeden ve buna latince ‘kırıklı’ anlamına gelen ‘fractus’ sözünden türettiği ‘fractal’ adını veren kişidir. Kendisinin tanımladığı ünlü ‘Mandelbrot Kümesi’, belki de dünyanın en meşhur geometrik şekillerinden birisidir.

Fraktal geometri, bildiğimiz Euklid (Öklid) geometrisinden oldukça farklıdır. Euklid geometrisi, okullarda okuduğumuz, üniversite sınavlarında karşımıza çıkan sıfır, bir iki ve üç boyutlu geometrik şekillerle ilgilenir. Mandelbrot’un fraktalleri ise, kesirli boyutlara sahip olmaları açısından, geleneksel geometriden kökten farklı bir yapı sergiler. Matematiğe çok girmeden bunu şöyle örneklendirebiliriz: Elinizde bir sayfa kağıt olduğunu ve bunun iki boyutlu olduğunu düşünün (aslında kağıt, kalınlığı da olan üç boyultu bir nesnedir ama, şimdilik kalınlıksız iki boyutlu bir yüzey düşünüyoruz). Kağıdı elinizde o kadar çok buruşturup sıkıştırıyorsunuz ki, artık son derece karmaşık hale gelmiş bu iki boyutlu yüzeyi ‘iki boyutlu’ olarak nitelemek gittikçe imkansızlaşıyor. Üç boyutlu olduğunu da iddia edemiyorsunuz, zira elinizdeki ne kadar buruşmuş olursa olsun, iki boyutlu bir yüzeydir aslında. Dolayısıyla, buruşma miktarı arttıkça, 2.05, 2.28, 2.4 gibi kesirli boyutlara sahip bir yüzey şekli elde etmeye başlarsınız. İşte fraktallerdeki kesirli boyut kavramı da buna benzer bir karmaşıklığın neticesinde ortaya çıkar. Aslında doğada hakim olan geometri de işte bu ‘fraktal geometri’dir...

Doğadaki biçimler gerçekten de geleneksel geometrinin bize öğrettiğinden çok farklıdır. Geleneksel (Euklid’çi) geometri daha ziyade idealize edilmiş soyutlamalardan oluşuruken, tabiattaki biçimler çok daha karmaşıktırlar. Yerküreyi 6-7 kez dolaşabilecek kan damarlarını ve bir kaç tenis kortu kadar alan kaplayan akciğer hava keseciklerini bu küçücük vücudumuza; açıldığında 2 metreyi aşkın bir uzunluğa erişen DNA molekülümüzü 100 trilyon hücremizin her birindeki bir kaç mikrometrelik (milimetrenin binde biri) çekirdeğin içine paketlenmesinin ardında, işte bu ‘fraktal’ kurallar yatmaktadır.

Fraktal özelliklere sahip bir geometrik şekli evinizde kendi başınıza elde etmenin bu gün için en kolay yolu, internette rahatlıkla bulunabilen hazır bilgisayar programlarından birisini kullanmaktır (fractal explorer). Zira her ne kadar basit olursa olsun, bir ‘fraktal’ ortaya çıkarmak, matematiksel bir dizi işlem serisi (iterasyonlar) gerektirir ki, bu tekrarlayan işlem serileri, tam da bilgisayarlara göre bir iştir. Örneğin Mandelbrot Kümesi aslında, ‘karmaşık sayılar’ı da içeren ve kendi sonucunu her tekrarda ‘giriş verisi’ olarak kullanan bir iterasyon, yani tekrar tekrar hesaplama işlemidir. Bu hesaplama sonucu elde edilen kapalı noktalar kümesi, alanı sonlu, fakat kenar uzunluğu sonsuz bir küme olarak tüm fraktallerin –tabir yerindeyse- atasıdır.

Fraktallerin bir başka çarpıcı özelliği, doğada çokça rastladığımız ‘kendine benzeme’ (self similarity) özelliğidir. Herhangi bir iterasyon dizgesi ile oluşturulan bir fraktal biçim, aynı matematiksel formül çekirdeğinin defalarca üst üste tekrarlanması ile ortaya çıktığından, ana kümenin şekli, küme kenarlarının mikroskobik detaylarında dahi benzer görünüm ve biçimlerde tekrarlanır.

Tabiatta da bu durumla sık sık karşılaşırız:
Örneğin ağaçların bir çok tipinde, dal ve köklerdeki saçaklanma biçimleriyle; dalların yan dallara ayrılma biçimlerinin, yaprakların çıkış noktalarının ve yapraklar üzerindeki damarların dallanış biçimlerinin hep birbirine benzer bir kalıp izlediğine belki de daha önce dikkat etmişsinizdir. Daha çarpıcı bir örnek olarak, atom-altı düzeyi de düşünebiliriz. Bu düzeyde ulaştığımız mikro-alem, aynen uzay boşluğu gibi karanlık, nisbi olarak korkunç mesafelerle birbirlerinden ayrılmış bileşenlerden (elektronlar - protonlar vb.) oluşan bir boşluktur ve atomun ardında, yeni bir ‘uzay boşluğu’, farklı ölçeklerle de olsa bizi bekler gibidir! İşte bu özellikler, fraktal geometrinin sadece ağlenceli bir oyun olmaktan ziyade, hayatın kendisini daha iyi anlamamızda yardımcı bir araç olarak kullanılması konusunda bizi defaatle ikaz ediyor.

Yapısındaki bıktırıcı ve binlerce tekrara dayalı matematiksel altyapıya rağmen fraktal geometri, özellikle günümüz yazılım teknolojisinin nimetleriyle de birleşince artık oldukça yaygınlaşmış durumda. Günümüzde fraktalleri oluşturmak için uzmanlığa gerek olmadığı gibi, güzelliklerini ve bize anlattıklarını anlayabilmek/takdir edebilmek için matematik dehası olmak gerekmiyor. Tek şart, insanî bir merak ve iştiyak sahibi olmak; hepsi o kadar.

Sinan Canan
2005/Kırmızı Çizgi Dergisi; Sayı 3

BEĞEN Paylaş Paylaş

Tanrı varsa eğer, ruhumu kutsasın... Ruhum varsa eğer!

Cevapla

FoReVeR LoVe

Ziyaretçi

6 Nisan 2010 Mesaj #3

Ziyaretçi

Fraktal Geometri Nedir?

İlk matematiksel fraktal kavramı 1861 de keşfedildi. Karl Weierstrass sürekli fakat hiçbir noktada diferensiyellenebilir olmayan , yani köşe noktalarından oluşan bir eğri üzerindeki değişmeleri araştırken, hiçbir noktada değişme oranının bulunamayacağı kanaati ile sarsılmıştır. Fraktal kelimesini Weierstrass bu cins eğriler için ilk defa kullanmıştır.

Matematik anlamda ilk çalışılan fraktal, Cantor Cümlesidir. Cantor (1845-1918) Halle Üniversitesi'ndeyken matematiğin temel konularından olan ve günümüzde Cümle Teorisi olarak adlandırılan alanı kuran bir Alman matematikçidir.

Cantor cümlesi ile ilgili ilk çalışma 1883 de basılmış [G. Cantor, Über Unendliche, lineare punktmannigfaltigkeiten V, Mathematische Annalen 21 (1883) 545-591] ve bazı özel cümleler için örnek olarak gösterilmiştir. Cantor cümlesi hiçbir yerde yoğun olmayan, mükemmel (perfect) alt cümlelere bir örnektir. Fraktalların tarihi gelişiminde Cantor, Sierpinski, Von Koch, Peano gibi matematikçiler tarafından oluşturulan fraktallar matematiksel canavarlar olarak adlandırılır. Matematiksel canavarların bahçesinde veya ilk fraktalların ortaya çıktığı zamanlarda Cantor cümlesi görünüş açısından diğerlerinden daha az gösterişli olmasına ve diğerlerine göre doğal yoruma daha uzak olmasına rağmen oldukça önemlidir. Cantor cümlesinin, matematiğin pek çok alanında özelikle Kaotik Dinamik Sistemlerde önemli rol oynadığı ve pek çok fraktallar (Julia cümleleri gibi) için de gerekli bir model olduğu görülmektedir.

Etrafımızda, parlak, tuhaf, güzel şekilli cisimler görürüz. Bunlara Fraktal denir. Gerçekten bunlar nedir?

İnternette fraktallar hakkında çok fazla bilgi vardır, fakat bu bilgilerin büyük kısmı ya güzel resimler veya yüksek seviyeli matematiksel kavramlarla ilgilidir. Dolayısıyla kolayca anlaşılır bir ifade ile diyebiliriz ki fraktallar tuhaf resimleri olan cisimler, matematiksel nesnelerdir. Okulda karşılaştığımız matematiğin çoğu eski bilgilerdir. Örneğin, geometride karşılaştığımız çemberler, dörtgenler ve üçgenler M.Ö. 300 üncü yıllarında Öklid tarafından ortaya konulmuştur. Buna rağmen Fraktal Geometri daha çok yenidir. Fraktallar üzerinde matematikçiler tarafından araştırmalar son 25 yıldır başlamış bulunmaktadır.

BEĞEN Paylaş Paylaş

Cevapla

nötrino

Yasaklı

19 Kasım 2011 Mesaj #4

Yasaklı

Mandelbrot Fraktalleri

Kaos teorisinin diğer bir öncüsü, IBM’de çalışan bir matematikçi olan Benoit Mandelbrot, farklı bir matematik tekniği kullandı. IBM için çalışan bir araştırmacı sıfatıyla, geniş bir çeşitlilik gösteren doğadaki “rastlantısal” süreçlerdeki “desenleri” araştırdı ve buldu. Örneğin telefon haberleşmesinde her zaman varolan fon “gürültüsünün” önceden kestirilmesi bütünüyle imkânsız olan ya da kaotik olan, ama yine de matematiksel olarak tanımlanabilen bir desen sergilediğini keşfetti. Mandelbrot IBM’deki bilgisayarları kullanarak, kaotik sistemleri, sadece en basit matematiksel kurallardan yararlanarak grafiksel olarak üretebilmişti. “Mandelbrot kümeleri” olarak bilinen bu resimler sonsuz bir karmaşıklık gösteriyordu, bu resimlerin herhangi bir kısmı daha ince ayrıntıları görmek için “büyütüldüğünde”, sınırsız olarak görünen muazzam çeşitlilik devam ediyordu.

Mandelbrot kümeleri belki de şimdiye kadar görülen en karmaşık matematiksel nesne veya model olarak tanımlanmıştı. Yine de kendi yapısı içerisinde hala desenler mevcuttu. Ölçek defalarca “büyütülerek” daha ince ayrıntılara bakıldığında (tüm yapı belirli bir matematiksel kurallar kümesine dayandığından bilgisayarın sayısız defa yapabileceği bir şey) farklı ölçeklerde düzenli tekrarların –benzerliklerin– varolduğu görülebildi. “Düzensizliğin derecesi” farklı ölçeklerde aynıydı. Mandelbrot düzensizliğin içinde besbelli olan desenleri tanımlamak için “fraktal” ifadesini kullandı. Matematiksel kurallar üzerinde ufak tefek değişiklikler yaparak çeşitli fraktal şekiller yapmayı başardı. Böylece herhangi bir ölçekte (herhangi bir büyültme oranında) her zaman aynı dereceden “düzensizliği” veya “kıvrımlaşmayı” sergileyen bir kıyı şeridini bilgisayarında simüle etmeyi başardı.

Mandelbrot kendi bilgisayar ağırlıklı sistemlerini, farklı ölçeklerde aynı deseni defalarca yineleyen fraktal biçimli geometri örnekleriyle de karşılaştırdı. Örneğin Menger Süngerinde, gerçek katı hacmi sıfıra yaklaşırken, iç yüzey alanı sonsuza gider. Burada, sanki düzensizlik derecesi süngerin yer kaplamaktaki verimliliğine tekabül etmektedir. Bu göründüğü kadar cazip olmayabilir, çünkü Mandelbrot’un da gösterdiği gibi doğada fraktal geometrinin birçok örneği vardır. Nefes borusunun iki bronş oluşturacak şekilde dallanması ve bu dallanmanın bronşlarda aşağılara doğru ciğerlerdeki minik hava geçitleri düzeyine kadar yinelenmesi, fraktal olduğu gösterilebilecek olan bir desen izler. Aynı şekilde kan damarlarının dallanmasının da fraktal olduğu gösterilebilir. Diğer bir deyişle, hangi ölçekte incelenirse incelensin yinelenen bir geometrik dallanma deseni, bir “kendine benzerlik” söz konusudur.

Doğadaki fraktal geometri örnekleri hemen hemen sınırsızdır ve Doğanın Fraktal Geometrisi adlı kitabında Mandelbrot tam da bunu kanıtlamak istemişti. Normal bir kalp atışları spektrumunun, belki de kalp kaslarındaki sinir liflerinin fraktal düzenlenişinden ötürü, fraktal yasalar izlediği bulunmuştur. Aynı durum bir şizofreni özelliği olan gözün istem dışı hızlı hareketleri için de doğrudur. Bu yüzden fraktal matematik, fizyoloji ve deprem çalışmalarından metalürjiye kadar uzanan disiplinleri içeren çeşitli bilim alanlarında bugün rutin bir biçimde kullanılmaktadır.

Kaosun deterministik temelinin diğer göstergeleri, faz geçişleri üzerine çalışmalarda ve matematik modelleyicilerin “çekici” olarak adlandırdıkları şeyler yardımıyla gösterilmişti. Faz geçişlerinin birçok örneği vardır. Bu, bir sıvının “laminer” akıştan türbülanslı akışa geçişi anlamına gelebileceği gibi, katının sıvıya ya da sıvının gaza dönüşümü veya bir sistemin iletkenlikten “süper iletkenliğe” geçişi anlamına da gelebilir. Bu faz değişimlerinin teknolojik tasarım ve inşa alanında son derece önemli sonuçları olabilir. Örneğin bir uçak, kanadı üzerindeki hava akışı laminer akıştan türbülanslı akışa dönüşürse irtifa kaybedecektir; aynı şekilde suyu pompalamak için gereken basınç borudaki akışın türbülanslı olup olmamasına bağlı olacaktır.

Faz-ölçek diyagramları ve çekicilerin kullanımı, rastlantısal gözüken sistemlerde geniş bir uygulama alanı bulan bir diğer matematiksel aracı temsil eder. Diğer kaos çalışmalarında olduğu gibi, elektrik osilatörlerini, akışkan dinamiğini ve hatta küresel yıldız kümelerindeki yıldızların dağılımını içeren çeşitli araştırma programları alanında da “garip çekiciler” olarak anılan, ortak desenlerin mevcut olduğu keşfedilmiştir. Bu çeşitli matematiksel araçların tümü –periyot katlanması, fraktal geometri, garip çekiciler– kaotik dinamiği inceleyen farklı araştırmacılar tarafından farklı zamanlarda geliştirildi. Ama hepsinin sonuçları aynı yöne işaret etmektedir: şimdiye dek rastlantısal olarak düşünülen şeylerin altında matematiksel bir yasallığın yattığına.

Mitchell Feigenbaum adlı bir matematikçi, birkaç ipucunu bir araya getirerek kaosun “evrensel teorisi” olarak adlandırdığı teorisini geliştirdi. Gleick’ın söylediği gibi “teorisinin, düzen ve türbülans arasında geçiş durumunda olan sistemlere ilişkin doğal bir yasayı ifade ettiğine inandı... evrenselliği sadece nitel değil, aynı zamanda niceldi de... sadece desenlere değil kesin sayılara da ulaşmıştı.” Marksistler, niceliğin niteliğe dönüşümü olarak bilinen diyalektik yasayla buradaki benzerliği fark edeceklerdir. Bu düşünce, değişimin ölçülebilir olduğu aşağı yukarı tedrici bir gelişim döneminden, değişimin o denli “devrimci”, “sıçrama”nın o denli büyük oluşu sayesinde sistemin bütün “niteliği”nin değiştiği bir sonraki döneme dönüşümünü anlatır. Gleick’ın burada kavramları benzer bir anlamda kullanışı, modern bilimsel teorinin materyalist diyalektiğe doğru sendeleyerek de olsa ilerlediğinin bir başka göstergesidir.

Yeni bilimin temel kalkış noktası, onun dünyayla gerçekte olduğu gibi, yani sürekli olarak değişen dinamik bir sistem olarak ilgilenmesidir. Klasik lineer matematik, sabit ve değişmez kategorilerle iş gören biçimsel mantık gibidir. Yaklaşım olarak yeterince sağlamdır ama gerçekliği yansıtmaz. Ne var ki diyalektik, değişimin ve süreçlerin mantığıdır ve bu nedenle biçimcilik karşısında büyük bir ilerlemeyi temsil eder. Aynı şekilde kaos matematiği de, hayatın tatsız düzensizliklerini ihmâl eden, ziyadesiyle “gerçekdışı” bilimden ileriye doğru atılmış bir adımdır.

Kaynak:Aklın İsyanı/Alan Woods,Ted Grant(Kaostan Çıkan Düzen)

BEĞEN Paylaş Paylaş

Cevapla

Cevap Yaz