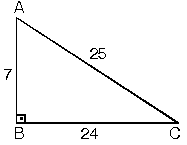
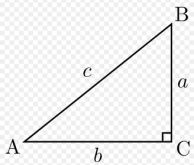
Bir açısının ölçüsü 90° olan üçgene dik üçgen denir. Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir. Hipotenüs üçgenin daima en uzun kenarıdır. şekilde, m A) = 90°
[BC] kenarı hipotenüs
[AB] ve [AC] kenarları dik kenarlardır.
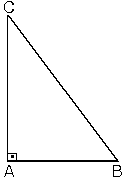
Dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir. ABC üçgeninde m A)= 90°
a2=b2+c2
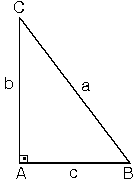 1. (3 - 4 - 5) Üçgeni
1. (3 - 4 - 5) Üçgeni
Kenar uzunlukları (3 - 4 - 5) sayıları veya bunların katı olan bütün üçgenler dik üçgendir. (6 - 8 - 10), (9 - 12 - 15),
gibi
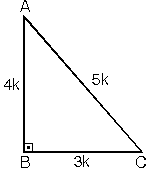 2. (5 - 12 - 13) Üçgeni
2. (5 - 12 - 13) Üçgeni
Kenar uzunlukları (5 - 12 - 13) sayıları ve bunların katı olan bütün üçgenler dik üçgenlerdir. (10 - 24 - 26), (15 - 36 - 39),
gibi.

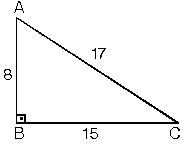
- Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir.
- Kenar uzunlukları 7, 24, 25 sayıları ile orantılı olan üçgenler dik üçgenlerdir.
 3. İkizkenar dik üçgen
3. İkizkenar dik üçgen
ABC dik üçgen |AB| = |BC| = a |AC| = aÖ2
m(A) = m(C) = 45° İkizkenar dik üçgende hipotenüs dik kenarların Ö2 katıdır.
4. (30° 60° 90°) Üçgeni
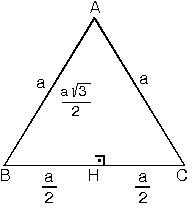
ABC eşkenar üçgeni yükseklikle ikiye bölündüğünde ABH ve ACH (30° - 60° - 90°) üçgenleri elde edilir.
|AB| = |AC| = a
|BH| = |HC| =
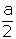 pisagordan
pisagordan 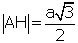
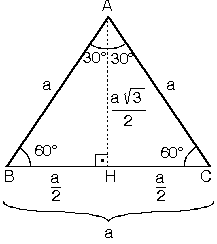 (30° - 60° - 90°) dik üçgeninde
(30° - 60° - 90°) dik üçgeninde; 30°'nin karşısındaki kenar hipotenüsün yarısına eşittir. 60° nin karşısındaki kenar,
30° nin karşısındaki kenarın Ö3 katıdır.
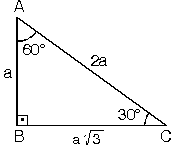
5. (30° - 30° - 120°) Üçgeni
(30° - 30° - 120°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 120° lik açının karşısındaki kenar aÖ3 olur.
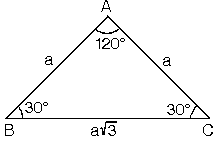
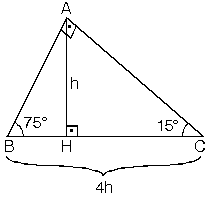
6. (15° - 75° - 90°) Üçgeni
(15° - 75° - 90°) üçgeninde hipotenüse ait yükseklik |AH| = h dersek, hipotenüs
|BC| = 4h olur. Hipotenüs kendisine ait yüksekliğin dört katıdır.
Dik üçgenlerde hipotenüse ait yüksekliğin verildiği durumlarda benzerlikten kaynaklanan öklit bağıntıları kullanılır.
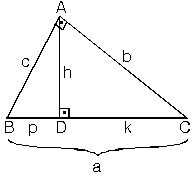 1.
1. Yüksekliğin hipotenüste ayırdığı parçaların çarpımı yüksekliğin karesine eşittir.
h2 = p.k 2. b2 = k.a c2 = p.a
3. ABC üçgeninin alanını iki farklı şekilde yazıp eşitlediğimizde
a.h =b.c
- Yukarıda anlatılan öklit bağıntıları kullanılarak
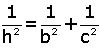 elde edilir.
elde edilir.
Genellikle bu öklit bağıntısını kullanmak yerine, yukarıdaki öklit bağıntıları ve pisagor bağıntısını kullanarak çözüme gideriz.
İkizkenar üçgenin tepe açısından tabanına çizilen yükseklik, hem açıortay, hem de kenarortaydır.
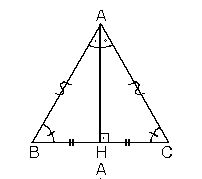 1.
1. Bir üçgende, açıortay aynı zamanda yükseklik ise bu üçgen ikizkenar üçgendir.
|AB| = |AC|
|BH| = |HC|
m(B) = m(C)
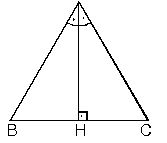 2.
2. Bir üçgende, açıortay aynı zamanda kenarortay ise bu üçgen ikizkenar üçgendir.
|AB| = |AC|,
[AH] ^ [BC]
m(B) = m(C)
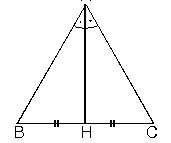 3.
3. Bir üçgende, yükseklik aynı zamanda kenarortay ise bu üçgen ikizkenar üçgendir.
|AB| = |AC|
m(BAH) = m(HAC)
m(B) = m(C)
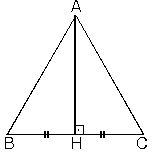
İkizkenar üçgende açıortay, kenarortay ve yüksekliğin aynı olması birçok yerde karşımıza çıktığından çok iyi bilinmesi gereken bir özelliktir.
4. İkizkenar üçgende ikizkenara ait yükseklikler eşittir. Bu durumda yüksekliklerin kesim noktasının ayırdığı parçalarda eşit olur.
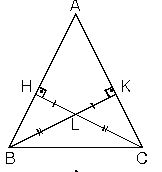 5.
5. İkizkenar üçgende ikizkenara ait kenarortaylar ve kenarortayların kesim noktasının ayırdığı parçalar da birbirine eşittir.
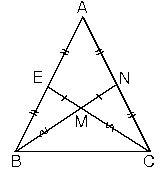 6.
6. İkizkenar üçgende eşit açılara ait açıortaylar da eşittir. Açıortaylar birbirini aynı oranda bölerler.
7. İkizkenar üçgende ikiz olmayan kenar üzerindeki herhangi bir noktadan ikiz kenarlara çizilen dikmelerin toplamı, ikizkenarlara ait yüksekliği verir.
|AB| = |AC| Þ |LC| = |HP| + |KP|
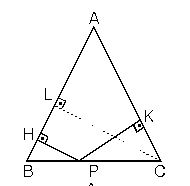 8.
8. İkizkenar üçgende tabandan ikiz kenarlara çizilen paralellerin toplamı, ikiz kenarların uzunluğuna eşittir.
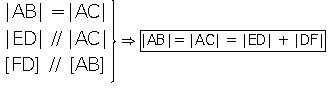
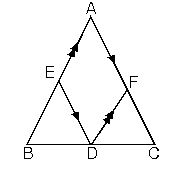
EŞKENAR ÜÇGEN 1. Eşkenar üçgende bütün açıortay, kenarortay yükseklikler çakışık ve hepsinin uzunlukları eşittir.
nA = nB = nC = Va = Vb = Vc = ha = hb = hc
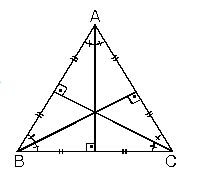 2.
2. Eşkenar üçgenin bir kenarına a dersek yük seklik
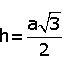
Bu durumda eşkenar üçgenin alanı

- yükseklik cinsinden alan değeri
Alan(ABC) =
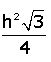 3.
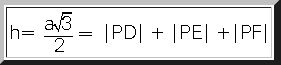
3. Eşkenar üçgenin içindeki herhangi bir noktadan kenarlara çizilen dik uzunlukların toplamı, eşkenar üçgene ait yüksekliği verir. Bir kenarı a olan eşkenar üçgende;
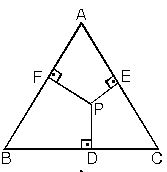 4.
4. Eşkenar üçgenin içindeki herhangi bir noktadan kenarlara çizilen paralellerin toplamı bir kenar uzunluğuna eşittir.
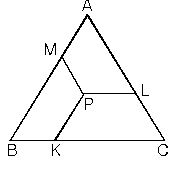
Bir kenarı a olan ABC eşkenar üçgeninde
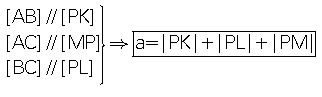
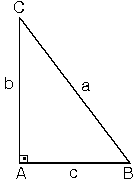
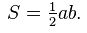
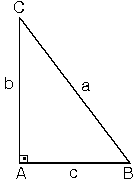

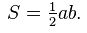

 Dik üçgen ve özellikleri
Dik üçgen ve özellikleri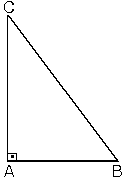
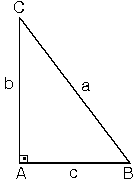
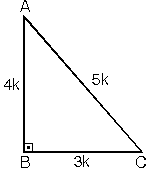



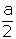
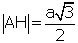

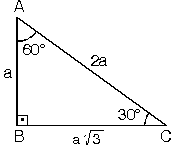
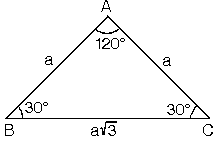


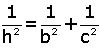 elde edilir.
elde edilir.






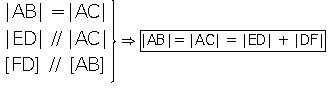


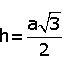 Bu durumda eşkenar üçgenin alanı
Bu durumda eşkenar üçgenin alanı 

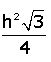



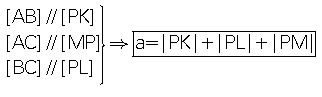
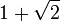 cm olur. İspatı ise 67,5°'lik açıyı 45° ve 22,5° şeklinde parçalayarak yapılır. Bu şekilde altta oluşan ikizkenar dik üçgende alt dik kenar 1 cm olursa hipotenüs
cm olur. İspatı ise 67,5°'lik açıyı 45° ve 22,5° şeklinde parçalayarak yapılır. Bu şekilde altta oluşan ikizkenar dik üçgende alt dik kenar 1 cm olursa hipotenüs 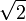 cm olur. Yukarıda oluşacak ikizkenar üçgende de parçalanan kenarın diğer üst tarafı hipotenüse eşit olur. Alt parçası da ikizkenar dik üçgenden dolayı 1 cm bulunacağından
cm olur. Yukarıda oluşacak ikizkenar üçgende de parçalanan kenarın diğer üst tarafı hipotenüse eşit olur. Alt parçası da ikizkenar dik üçgenden dolayı 1 cm bulunacağından 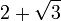 cm olur. İspatı ise 22,5-67,5-90 üçgenindeki gibidir. Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir.
cm olur. İspatı ise 22,5-67,5-90 üçgenindeki gibidir. Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir. katına eşittir
katına eşittir


