ÜÇGEN
Kesişimleri boş olmayıp tek bir nokta da olmayan üç ışının kapattığı geometrik şekil ya da üç kenarı olan çokgen.
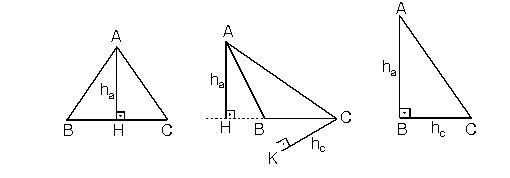
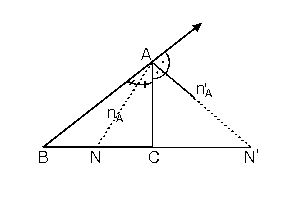
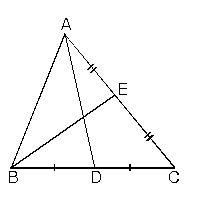
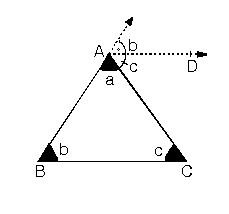
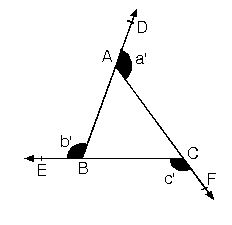
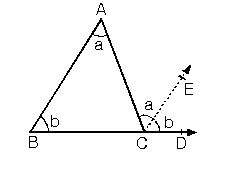
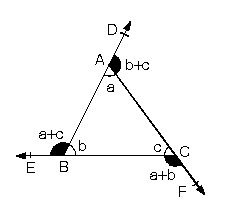
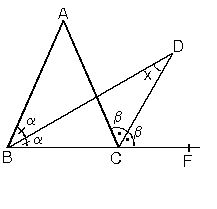
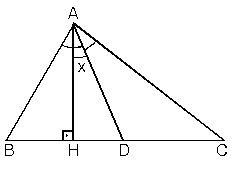
Işınların kesişimine üçgenin köşeleri, köşeler arasındaki parçalara da üçgenin kenarları denir. Köşeler büyük harflerle, karşılarındaki kenar da bunların küçük harfleriyle adlandırılır. Üçgenin iç açıları ve kenarları "temel eleman", yükseklik (bir köşeden karşı kenara indirilen dikme), kenarortay (bir köşeyi karşı kenarın ortasına birleştiren doğru) ve açıortay da (bir açıyı iki eş açıya bölen ve köşedenkarşı kenara kadar uzanan ışın) "yardımcı eleman" olarak bilinir.
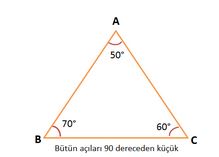
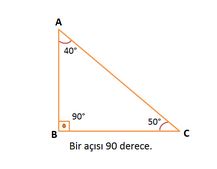
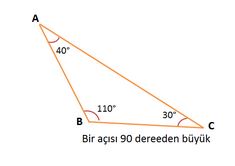
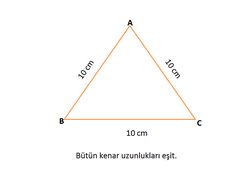
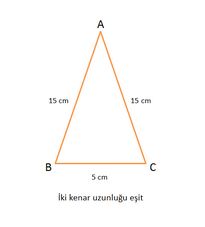
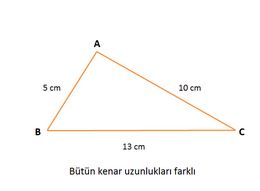
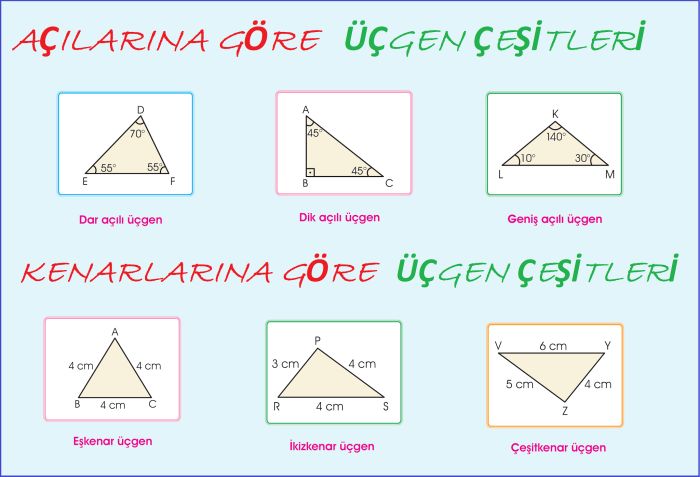
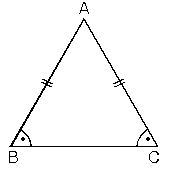
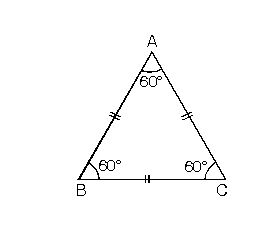
Üçgenler kenarları bakımından "eşkenar üçgen" (üç kenarının uzunluğu eşit, tüm temel ve yardımcı elemanlar her köşe için aynıdır), "ikizkenar üçgen" (iki kenarın uzunluğu ve karşılarındaki açılar birbirine eşittir) ve "çeşitkenar üçgen" (üç kenarı ayrı uzunluktadır) gibi üç gruba; açıları bakımından da "dar üçgen" (açıları dar açıdır), "dik üçgen" (bir açısı dik açıdır) ve "geniş üçgen" (bir açısı geniş açıdır).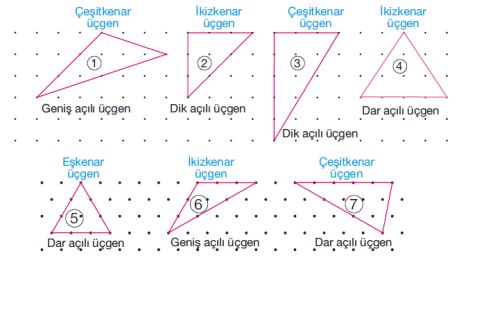
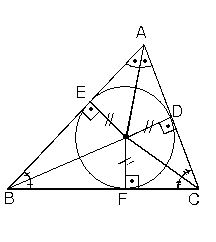
Gibi yine üç gruba ayrılırlar. Bir üçgende toplam üç yükseklik, üç kenarortay ve üç açıortay vardır. Bunlar kendi aralarında, tek bir noktada kesişirler. Yüksekliklerin kesim noktası "ortosantr" adıyla anılır. Dik üçgenlerde ortosantr, dik köşedir. Geniş üçgende ortosantr, üçgenin dış bölgesinde yer alır. Kenarortayların kesim noktası, üçgenin ağırlık merkezidir ve bu nokta, kenarlara yakın olup kenarortayları 1/3 oranında içten böler. Açıortayların kesim noktasıysa üçgenin iç teğet çemberinin merkezidir.
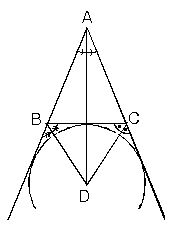
Bir iç açıortay ile öteki iki açının dış açıortaylarının kesim noktası da üçgenin dış teğet çemberinin (toplam 3 dış teğet çember vardır) merkezidir. Bir üçgenin alanı, herhangi bir kenar uzunluğuyla bu kenara ilişkin yüksekliğin çarpımının yarısıdır. Üçgen için başka alan formülleri de vardır. Örneğin iç teğet çemberinin yarıçapı r ve çevresi 2u olan üçgenin alanı "u.r"dir.
Kesişimleri boş olmayıp tek bir nokta da olmayan üç ışının kapattığı geometrik şekil ya da üç kenarı olan çokgen.
Sponsorlu Bağlantılar
Işınların kesişimine üçgenin köşeleri, köşeler arasındaki parçalara da üçgenin kenarları denir. Köşeler büyük harflerle, karşılarındaki kenar da bunların küçük harfleriyle adlandırılır. Üçgenin iç açıları ve kenarları "temel eleman", yükseklik (bir köşeden karşı kenara indirilen dikme), kenarortay (bir köşeyi karşı kenarın ortasına birleştiren doğru) ve açıortay da (bir açıyı iki eş açıya bölen ve köşedenkarşı kenara kadar uzanan ışın) "yardımcı eleman" olarak bilinir.
Üçgenler kenarları bakımından "eşkenar üçgen" (üç kenarının uzunluğu eşit, tüm temel ve yardımcı elemanlar her köşe için aynıdır), "ikizkenar üçgen" (iki kenarın uzunluğu ve karşılarındaki açılar birbirine eşittir) ve "çeşitkenar üçgen" (üç kenarı ayrı uzunluktadır) gibi üç gruba; açıları bakımından da "dar üçgen" (açıları dar açıdır), "dik üçgen" (bir açısı dik açıdır) ve "geniş üçgen" (bir açısı geniş açıdır).

Gibi yine üç gruba ayrılırlar. Bir üçgende toplam üç yükseklik, üç kenarortay ve üç açıortay vardır. Bunlar kendi aralarında, tek bir noktada kesişirler. Yüksekliklerin kesim noktası "ortosantr" adıyla anılır. Dik üçgenlerde ortosantr, dik köşedir. Geniş üçgende ortosantr, üçgenin dış bölgesinde yer alır. Kenarortayların kesim noktası, üçgenin ağırlık merkezidir ve bu nokta, kenarlara yakın olup kenarortayları 1/3 oranında içten böler. Açıortayların kesim noktasıysa üçgenin iç teğet çemberinin merkezidir.
Bir iç açıortay ile öteki iki açının dış açıortaylarının kesim noktası da üçgenin dış teğet çemberinin (toplam 3 dış teğet çember vardır) merkezidir. Bir üçgenin alanı, herhangi bir kenar uzunluğuyla bu kenara ilişkin yüksekliğin çarpımının yarısıdır. Üçgen için başka alan formülleri de vardır. Örneğin iç teğet çemberinin yarıçapı r ve çevresi 2u olan üçgenin alanı "u.r"dir.
MsXLabs.org & Morpa Genel Kültür Ansiklopedisi
BAKINIZ Dik üçgen ve özellikleri
Son düzenleyen Safi; 7 Ocak 2017 23:14
"İnşallah"derse Yakaran..."İnşa" eder YARADAN.

 Üçgen
Üçgen