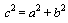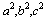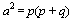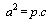Arama

Dik Üçgen (Vikipedi)

Güncelleme: 7 Nisan 2016 Gösterim: 23.013 Cevap: 3
Konu Kapalı
ThinkerBeLL - avatarı
ThinkerBeLL
VIP VIP Üye
29 Haziran 2009       Mesaj #1
ThinkerBeLL - avatarı
VIP VIP Üye
Dik Üçgen
Vikipedi, özgür ansiklopedi
Bir dik üçgen
Ad: 200pxtrianglerightsvg.png Gösterim: 956 Boyut: 2.6 KB
Dik üçgen, iç açılarından biri 90° olan üçgendir. Çemberde çapı gören çevre açı 90°'dir.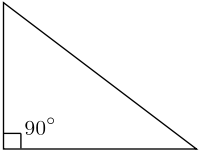
Sponsorlu Bağlantılar

Konu Başlıkları
  1. Dik Üçgenlerle İlgili Bağıntılar
    • 1.1. Pisagor Teoremi
  2. Özel Dik Üçgenler
    • 2.1. Açıya Göre
      • 2.1.1. 45 - 45 - 90 Üçgeni
      • 2.1.2. 30 - 60 - 90 Üçgeni
      • 2.1.3. 22,5 - 67,5 - 90 Üçgeni
      • 2.1.4. 15 -75 - 90 Üçgeni

Tanrı varsa eğer, ruhumu kutsasın... Ruhum varsa eğer!
ThinkerBeLL - avatarı
ThinkerBeLL
VIP VIP Üye
29 Haziran 2009       Mesaj #2
ThinkerBeLL - avatarı
VIP VIP Üye
Dik Üçgen
Vikipedi, özgür ansiklopedi
Sponsorlu Bağlantılar

Özel Dik Üçgenler

Açıya Göre
Ad: 324pxisoscelesrighttria.png Gösterim: 907 Boyut: 4.5 KB
1. 45-45-90 Üçgeni

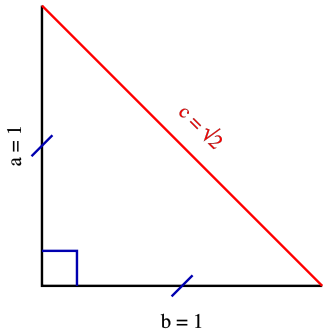
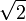45-45-90 üçgeni bir ikizkenar dik üçgendir. Üçgenin dik kenarları birbirine eşit ve hipotenüsü dik kenarların Ad: ef5590434a387b3c4427e09.png Gösterim: 6088 Boyut: 292 Byte katıdır. Oran aşağıdaki gibidir: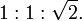
Ad: 2d7c122050813ac77a1c5eb.png Gösterim: 741 Boyut: 395 Byte
İspatı ise çok basittir. Bir dik kenara 1 cm denilirse, ikizkenarlıktan dolayı diğer dik kenar da 1 cm olmak zorundadır. Pisagor Teoremi'nden de hipotenüs Ad: ef5590434a387b3c4427e09.png Gösterim: 6088 Boyut: 292 Byte çıkar.

2. 30-60-90 Üçgeni
30-60-90 üçgeni ve ispatı
Ad: 184px306090svg.png Gösterim: 1069 Boyut: 6.8 KB
Açıları 30-60-90 olan bir dik üçgende hipotenüs, 30°'nin karşısındaki kenar ve 60°'nin karşısındaki kenar arasında sırasıyla aşağıdaki oran vardır:
Ad: 812e6995d6f1282bb97e20e.png Gösterim: 691 Boyut: 445 Byte
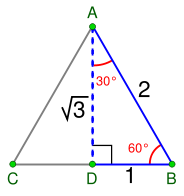
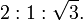
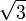Yani 30°'nin karşısındaki kenar hipotenüsün yarısı ve 60°'nin karşısındaki kenar da 30°'nin karşısındaki kenarın Ad: 7d2db2b2c90be143cb85c10.png Gösterim: 674 Boyut: 294 Byte katıdır. İspatı ise eşkenar üçgen vasıtasıyla yapılır. Kenarları 2 cm olan bir eşkenar üçgende köşeden indirilen dikme kenarı iki eş parçaya bölecektir. Aynı zamanda da açıortay olacaktır. Kenarortay olduğu için oluşan dik üçgenin alt dik kenarı 1 cm olacaktır. Açıortay olduğu için de dik üçgenin bir açısı 30° olacaktır. Eşkenar üçgenin bir kenarı, oluşan dik üçgenin hipotenüsü olacağından yapılacak Pisagor bağıntısı ile de indirilen dikme Ad: 7d2db2b2c90be143cb85c10.png Gösterim: 674 Boyut: 294 Byte cm bulunacaktır.

3. 22,5-67,5-90 Üçgeni

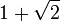Bu üçgende ise 22,5°'lik açının karşısındaki dik kenar 1 cm ise, 67,5 cm'lik kenarın karşısındaki kenar Ad: d2bd03008ff3b16980c465b.png Gösterim: 7638 Boyut: 359 Byte cm olur. İspatı ise 67,5°'lik açıyı 45° ve 22,5° şeklinde parçalayarak yapılır. Bu şekilde altta oluşan ikizkenar dik üçgende alt dik kenar 1 cm olursa hipotenüs Ad: ef5590434a387b3c4427e09.png Gösterim: 6088 Boyut: 292 Byte cm olur. Yukarıda oluşacak ikizkenar üçgende de parçalanan kenarın diğer üst tarafı hipotenüse eşit olur. Alt parçası da ikizkenar dik üçgenden dolayı 1 cm bulunacağından Ad: d2bd03008ff3b16980c465b.png Gösterim: 7638 Boyut: 359 Byte elde edilir.

4. 15-75-90 Üçgeni
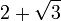Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar Ad: 5b94c53425824c1fb88a619.png Gösterim: 6080 Boyut: 418 Byte cm olur. İspatı ise 22,5-67,5-90 üçgenindeki gibidir. Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir.
Ayrıca bu üçgende hipotenüse indirilen dikme, hipotenüsün 1/4 katıdır.
Kenarlara göre özel dik üçgenler genelde okullarda soru yazılırken işlem kolaylığı sağlamak amacıyla kullanılır. Bazı özel üçgenler şunlardır:
  • 3 : 4 : 5
  • 6 : 8 : 10
  • 5 : 12 : 13
  • 8 : 15 : 17
  • 7 : 24 : 25
Bu üçgenlerin kenar uzunlukları aynı oranda artırılarak yine uygun dik üçgenler elde edilebilir (örneğin, 3-4-5 ve 6-8-10).
Tanrı varsa eğer, ruhumu kutsasın... Ruhum varsa eğer!
ThinkerBeLL - avatarı
ThinkerBeLL
VIP VIP Üye
29 Haziran 2009       Mesaj #3
ThinkerBeLL - avatarı
VIP VIP Üye
Dik Üçgen
Vikipedi, özgür ansiklopedi

Dik Üçgenlerle İlgili Bağıntılar

Pisagor Teoremi
Pisagor teoremi, herhangi bir dik üçgende kenarlar arasındaki bağıntıya verilen addır. Bu bağıntıya göre, dik kenarların karelerinin toplamı, hipotenüsün karesine eşittir.
Bunun ispatı şuna dayanmaktadır:
Ad: pt1.png Gösterim: 750 Boyut: 354 Byte
'c' uzunluğu hipotenüstür. 'a' ve 'b uzunlukları ise dik kenarlardır. Her kenardan birer kare oluşturulur. Bu karelerin alanları, kare alan formülüne dayalı olarak
Ad: pt2.png Gösterim: 743 Boyut: 335 Byte
şeklinde sıralanır. Böylece üç karenin köşelerinin birleşiminden oluşan bir dik üçgen oluşturulur. Oluşan üçgenin dik köşesinden hipotenüsün oluşturduğu karenin, hipotenüse paralel olan kenara indirilen dikme ile üçgen içerisinde Öklid bağıntısı kurulur. (Öklid bağıntısı benzerlikten ispatlanabilmektedir.)
Öklid'e göre;
Ad: pt3.png Gösterim: 751 Boyut: 407 Byte
yani, dik kenarlardan birinin karesi, dik açıdan hipotenüse indirilen dikmenin ayırdığı parçalardan kendisine komşu olan tarafın uzunluğu ile hipotenüsün tamamının çarpımına eşittir. Bu durumda;
Ad: pt4.png Gösterim: 736 Boyut: 329 Byte
olacaktır. Yani a kenarına ait karenin alanı, hipotenüse ait alanın dik açıdan indirilen dikmeyle ikiye ayırdığı alanlardan kendisine komşu olan alana eşit olacaktır. Bu durumu diğer kenar için de düşünürüz.
Ad: pt5.png Gösterim: 934 Boyut: 2.7 KB
olacaktır.

Ayrıca bakınız: Pisagor Teoremi
Tanrı varsa eğer, ruhumu kutsasın... Ruhum varsa eğer!
Safi - avatarı
Safi
SMD MiSiM
7 Nisan 2016       Mesaj #4
Safi - avatarı
SMD MiSiM
  • DİK ÜÇGEN
Bir açısının ölçüsü 90° olan üçgene dik üçgen denir. Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir. Hipotenüs üçgenin daima en uzun kenarıdır. şekilde, m A) = 90°
[BC] kenarı hipotenüs
[AB] ve [AC] kenarları dik kenarlardır.
46822d1459999601 dik ucgen ve ozellikleri dik3g1

DEVAMI Dik üçgen ve özellikleri
BEĞEN Paylaş Paylaş
Bu mesajı 1 üye beğendi.
SİLENTİUM EST AURUM
Konu Kapalı

Benzer Konular

10 Mayıs 2013 / ThinkerBeLL Matematik
3 Nisan 2015 / Misafir Cevaplanmış
7 Kasım 2012 / Misafir Soru-Cevap
22 Nisan 2015 / Misafir Cevaplanmış
7 Mayıs 2014 / Misafir Cevaplanmış


Fibonacci Dizisi
Üçgen

Kapat
Saat: 22:34 Hoş Geldiniz Ziyaretçi
Avatar Ücretsiz üye olarak sohbete ve
forumlarımıza katılabilirsiniz.
Üye olmak için lütfen tıklayınız.

Benzer Konular

10 Mayıs 2013 / ThinkerBeLL Matematik
3 Nisan 2015 / Misafir Cevaplanmış
7 Kasım 2012 / Misafir Soru-Cevap
22 Nisan 2015 / Misafir Cevaplanmış
7 Mayıs 2014 / Misafir Cevaplanmış
Son MesajlarYenile
Yükleniyor...