Ziyaretçi
Bağımlı ve bağımsız olay nedir, nasıl tanımlanır?
Bağımsız ve bağımlı olay ile ilgili sorular nasıl çözülür?
Bağımlı ve bağımsız olay ile ilgili çözümlü soru örnekleri nelerdir?
Bağımsız ve bağımlı olay ile ilgili sorular nasıl çözülür?
Bağımlı ve bağımsız olay ile ilgili çözümlü soru örnekleri nelerdir?
Bağımsız Olay
Bir olay, diğer bir olayın gerçekleşmesinden etkilenmiyorsa bu olay bağımsız olay olarak tanımlanır. Bağımsız olay, P( A )=P(A\B) ve P(AnB)=P( A ).P( B ) şeklinde ifade edilir!
Birden fazla olayın gerçekleşmesi birbirinden etkileniyorsa bu olaylar bağımlı olay olarak tanımlanır.Bağımlı olay P(A ve B)=P( A ).P(A'ya bağlı B) şeklinde ifade edilir!
Sponsorlu Baglantilar
- Örnek Soru: Bir madeni paranın ve zarın birlikte atılması olayında madeni paranın tura, zarın tek sayı gelme olasılığı kaçtır?
Çözüm: Madeni para olayı ile zar olayı bağımsız olaylardır. Madeni paranın tura gelmesi olayı A ve zarın tek sayı gelmesi olayı da B ile ifade edilirse sonuç, P(AnB)=P( A ).P( B ) => 1/2.3/6=1/4 bulunur!
Birden fazla olayın gerçekleşmesi birbirinden etkileniyorsa bu olaylar bağımlı olay olarak tanımlanır.Bağımlı olay P(A ve B)=P( A ).P(A'ya bağlı B) şeklinde ifade edilir!
- Örnek Soru: İçerisinde 2 mavi, 4 yeşil ve 4 gri top bulunan bir kutudan art arda ve geri bırakılmadan 2 top çekiliyor, çekilen topların ikisinin de gri gelme olasılığı kaçtır?
Çözüm: P(A ve B)=P( A ).P(A'ya bağlı B) => 4/10.3/9=2/15 bulunur!
Son düzenleyen nötrino; 9 Aralık 2015 11:12
Sebep: İç başlık düzeni!!

 Bağımlı ve bağımsız olayla ilgili soru cevap örnekleri verir misiniz?
Bağımlı ve bağımsız olayla ilgili soru cevap örnekleri verir misiniz? koşulunu sağlaması durumunda karşılıklı bağımsızdır. Bu olgu bağımsız olaylar için çarpım kuralı olarak adlandırılmaktadır.
koşulunu sağlaması durumunda karşılıklı bağımsızdır. Bu olgu bağımsız olaylar için çarpım kuralı olarak adlandırılmaktadır.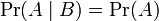
 (Pr( B) ≠ 0 olduğu sürece)biçiminde tanımlanmaktadır.
(Pr( B) ≠ 0 olduğu sürece)biçiminde tanımlanmaktadır. iken bu ifade
iken bu ifade olarak da yazılabilir.
olarak da yazılabilir. koşulunun sağlanması durumunda gerçekleşebilir. Başka bir deyişle, bir olay ya da onun tümleyeni neredeyse kesin olarak gerçekleşiyorsa bu olay kendinden bağımsızdır.
koşulunun sağlanması durumunda gerçekleşebilir. Başka bir deyişle, bir olay ya da onun tümleyeni neredeyse kesin olarak gerçekleşiyorsa bu olay kendinden bağımsızdır. Diğer taraftan, eğer X, Y ve Z sürekli rassal değişken iseler ve p ortak olasılık yoğunluk fonksiyonu bulunmakta ise; o halde X ve Y değişkenlerinin Z verilmişine koşullu bağımsız olmaları için şart şudur: Her x, y ve z gerçel sayılar için pZ(z) > 0 olursa
Diğer taraftan, eğer X, Y ve Z sürekli rassal değişken iseler ve p ortak olasılık yoğunluk fonksiyonu bulunmakta ise; o halde X ve Y değişkenlerinin Z verilmişine koşullu bağımsız olmaları için şart şudur: Her x, y ve z gerçel sayılar için pZ(z) > 0 olursa Bu demektir ki Y ve Z verilirse X için koşullu dağılım, sadece Z için dağılımın aynıdır. Sürekli halde de koşutlu olasılık yoğunluk fonksiyonları için de bir benzer denklem verilebilir.Olasılık bir çeşit hiç verilmiş olay olmayan koşutlu olasılık olduğu için, bağımsızlık koşutlu bağımsızlığın özel bir hali olarak görülebilir.
Bu demektir ki Y ve Z verilirse X için koşullu dağılım, sadece Z için dağılımın aynıdır. Sürekli halde de koşutlu olasılık yoğunluk fonksiyonları için de bir benzer denklem verilebilir.Olasılık bir çeşit hiç verilmiş olay olmayan koşutlu olasılık olduğu için, bağımsızlık koşutlu bağımsızlığın özel bir hali olarak görülebilir.
