Mantıkta Çözülüm Teorem İspatlama
Ziyaretçi
Çözülüm teorem ispatlama, mantık teoremlerinin ispatlanması için A. Robinson tarafından geliştirilmiş bir tekniktir. Bu tekniğin esası şudur:
Eğer “ve” bağı ile bağlı P1, ..., Pn önermelerinden bir Q önermesi dedüktif olarak çıkarılabiliyorsa, o zaman Q'nun değillemesini bu önermelere “ve” bağı ile kattığımız zaman bir çelişki elde ederiz. Sembollerle gösterecek olursak:
...çıkarımı geçerli ise,
...bir çelişkidir.
Bu yöntemin kullanılabilmesi için, P1, ..., Pn önermelerinin, eşdeğerlik dönüşümleri kullanılarak “birleşimli normal biçim” denilen bir biçime getirilmesi gerekir. Bu biçim sadece “değil”, “ve” ve “veya” mantıksal bağlarını içerir.
Örnek 1:
P -> Q ~P V Q ~P V Q
P P P
------ ------ ~Q
Q Q ------
Bu örnekte
şartlı önermesi yerine, eşdeğeri 
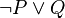konulmuştur ki bu, önermesinin normal biçimidir.
Örnek 2:
A -> B ~A V B ~A V B
B -> C ~B V C ~B V C
A A A
-------- --------- ~C
C C ---------
Çözülüm teorem ispatlama yöntemi, yüklemler mantığının teorem ispatlama problemlerinde de uygulanmaktadır. Yüklemler mantığında teorem ispatı sırasında bireysel sabitlerin değişkenlerin yerine konulmasına “birleştirme” denilir.
Örnek 3:
P(x,y) -> Q(x) ~P(x,y) V Q(x) ~P(a,y) V Q(a)
P(a,y) P(a,y) P(a,y)
-------------- --------------- ~Q(a)
Q(a) Q(a) ---------------
Eğer “ve” bağı ile bağlı P1, ..., Pn önermelerinden bir Q önermesi dedüktif olarak çıkarılabiliyorsa, o zaman Q'nun değillemesini bu önermelere “ve” bağı ile kattığımız zaman bir çelişki elde ederiz. Sembollerle gösterecek olursak:
Sponsorlu Bağlantılar
...çıkarımı geçerli ise,
...bir çelişkidir.
Bu yöntemin kullanılabilmesi için, P1, ..., Pn önermelerinin, eşdeğerlik dönüşümleri kullanılarak “birleşimli normal biçim” denilen bir biçime getirilmesi gerekir. Bu biçim sadece “değil”, “ve” ve “veya” mantıksal bağlarını içerir.
Örnek 1:
P -> Q ~P V Q ~P V Q
P P P
------ ------ ~Q
Q Q ------
Bu örnekte
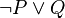şartlı önermesi yerine, eşdeğeri konulmuştur ki bu, önermesinin normal biçimidir.Örnek 2:
A -> B ~A V B ~A V B
B -> C ~B V C ~B V C
A A A
-------- --------- ~C
C C ---------
Çözülüm teorem ispatlama yöntemi, yüklemler mantığının teorem ispatlama problemlerinde de uygulanmaktadır. Yüklemler mantığında teorem ispatı sırasında bireysel sabitlerin değişkenlerin yerine konulmasına “birleştirme” denilir.
Örnek 3:
P(x,y) -> Q(x) ~P(x,y) V Q(x) ~P(a,y) V Q(a)
P(a,y) P(a,y) P(a,y)
-------------- --------------- ~Q(a)
Q(a) Q(a) ---------------
