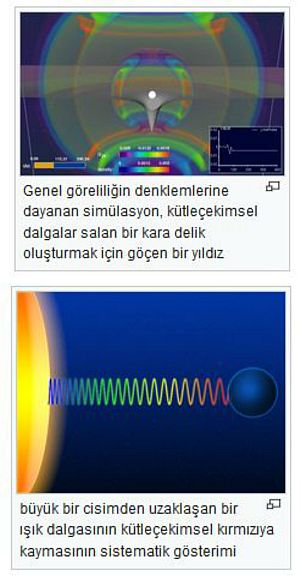
GENEL GÖRELİLİK KURAMI
Fiziksel kökenleri.
Sponsorlu Bağlantılar
Newtonun kütleçekimi etkileşmelerine getirdiği açıklamalar, olağanüstü doğrulukta sonuçlar veren en başarılı kuramlardan birini oluşturmaktadır. Newtonun kuramı, Güneşin gezegenleri ve gezegenlerin de uydularını çektiğini, bu karşılıklı çekimin uzaydaki çok büyük uzaklıklarda bile bir anda gerçekleştiğini öngörür; buna karşılık görelilik kavramları, hiçbir etkileşmenin ışık hızından daha hızlı yaylamayacağını öne sürer. Güneş sistemindeki gökcisimleri ışık hızının binde birinden düşük hızlarla hareket ettiklerinden, pratikte bunun bir önemi yoksa da, Newtonun anlık etki kavramı görelilik kuramının uzay-zaman kavramıyla temelden uyuşmazlık içindedir.
Maxwellin elektrik alanı kuramından elde edilen deneyimleri temel alan Einstein, ışık hızıyla yayılan ve Newton kuramının öngördüğü çekime hemen hemen eşit bir çekim ortamı yaratan bir kütleçekimi alanının varlığını öngördü. Bir kütleçekimi alanı kuramının matematiksel olarak elektrik ve magnetik alan kuramlarından daha kapsamlı olması gerektiği, daha başından belliydi. Elektrik alan kaynakları olan parçacık yükleri, onları ölçen aygıtların hareket durumlarından bağımsız değerlere sahiptir. Kütleçekimi alanının kaynağı olan parçacık kütlesi ise belirlendiği referans sistemine göre parçacığın hızına bağlı olarak değişir ve ayrı referans sistemlerinde ayrı değerler alır. Bu zorlaştırıcı etken, göreli kütleçekimi kuramını geliştirme uğraşısında ortaya bir belirsizlik çıkarır. Einstein bu sorunu eşdeğerlik ilkesine başvurarak çözmüştür.
Eşdeğerlik ilkesi.
Bir kütleçekimi alanında, örneğin yeryüzünde, kütlesi daha büyük olan bir cisme etkiyen kuvvetin de daha büyük olduğu günlük yaşamdan bilinir. Newton belirli bir çekim alanında bir efeme etkiyen kuvvet ile o cismin kütlesi arasındaki oranın, cismin kimyasal yapısına ve başka özelliklerine bakmaksızın, bütün cisimler için aynı olduğunu ve çekim alanında serbest düşüş yapan bütün cisimlerin aynı ivmeye (hızlanma hızı) sahip olduğunu belirlemişti. Yeryüzünde bu ivme saniyede yaklaşık 9,81 mdir.

Kütleçekimi etkisiyle hızlanma, bir uzay yolculuğu örneğiyle ele alınabilir. Uzay kapsülü süzülmeye geçtiğinde, aracın, astronotların ve araçtaki bütün cisimlerin ivmesi aynıdır yani birbirlerine göre ivmeleri yoktur. Bunun sonucu olarak görünüşte ağırlıksızlık ortaya çıkar. Astronotları kapsülün tabanına bastıran bir kuvvet kalmamıştır. Serbestçe inişe geçen uzay kapsülündeki nesnelerin davranışları, kapsül yıldızlar- arası uzayda tüm kütleçekimi alanlarının dışında eylemsizlik yasasına göre hareket ederken karşılaşacakları koşullardaki davranışlarından ayırt edilemez. Uzay kapsülü kütleçekimi bulunmayan bir ortamda roket motorları aracılığıyla yukarı doğru hızlandığında ise kapsül içindeki tüm cisimler, kapsül bir kütleçekimi alanında durgun durumdayken gösterecekleri davranışları gösterirler. Eşdeğerlik ilkesi, ivme kazanmış eylemsiz olmayan bir referans sistemine (örn. roketleri ateşlenmiş kapsül) gösterilen tepkiler ile kütleçekimi kuvvetleri arasında eşdeğerliği ve eylemsiz referans sistemleri ile serbest düşen yerel referans sistemleri arasındaki eşdeğerliği ortaya koyar.
Einstein, kütleçekimi alanlarının bulunduğu yerlerde, seçilen bir referans sisteminin eylemsiz olmayan karakterinden doğan etkilerle kütleçekiminin etkilerini ayırt edebilecek hiçbir yol bulunmadığını kanıtlamıştır. Genel görelilik kuramı, kütleçekimi alanının bu niteliğini temel olarak kabul etmiştir.
Uzay-zaman eğriliği
Minkowski uzay-zamanında eylemsiz referans sistemleri, Eukleidesçi geometrideki doğrulardan oluşan kartezyen koordinat sistemlerine benzer. Böyle bir koordinat sistemi bir düzleme her zaman yerleştirilebilir, ama bir küre yüzeyine uygulanamaz. Çünkü karelerden oluşan bir ızgarayı bir küre yüzeyine örtmek olanaklı değildir. Bu nedenle, düzlem düz bir yüzeydir, ama küre yüzeyi eğridir. Yüzeylerin kendi iç özelliklerinden kaynaklanan bu sınıflamaya göre silindir yüzeyi de düz bir yüzeydir, çünkü bir düzlem üzerine açındırılabilir yani karelerden oluşan bir ızgarayla örtülebilir.
Einstein kütleçekimi alanlarının (kütleçekimi yokken düz olan) uzay-zamanı eğrilttiğini ve eylemsiz sistemlerin bu nedenle oluşturulamayacağını öne sürdü. Bir parçacığın kütleçekimi etkisiyle uzayda ve zamanda eğrilen yörüngesi, (ancak düz uzaylarda ve uzay-zamanlarda var olabilen) doğru çizgilere değil, eğrilmiş bir uzay- zamanda var olabilecek en düz eğriye karşılık gelir; böyle eğriler jeodezik olarak adlandırılır. Yerin yüzeyi gibi küresel yüzeyler üzerindeki jeodezikler, içinde bulundukları düzlemler kürenin merkezinden geçen büyük çemberlerdir. Bunlar küre yüzeyine çizilebilecek eğriliği en az çizgilerdir, ayrıca yüzeydeki iki noktayı birleştiren en kısa yolu oluştururlar. Uzay-zamanda ise jeodezikler iki olguyu (bir parçacığın geçmişindeki iki anı) arada geçen zaman en büyük olacak biçimde birleştirirler.
Bir kütleçekimi alanı, uzay-zamanın eğriliğine yol açıyorsa, bu eğrilik hesaplarından kütleçekimi alanlarına ilişkin nicelikler saptanabilir. Eğriliği belirleyen bileşenler, matematikçi Bernhard Riemannın geliştirdiği eğrilik tensörleriyle hesaplanabilir.
Kuramın doğrulanması
Genel görelilik kuramının temel taşlarından biri sayılan eşdeğerlik ilkesi çok duyarlıklı deneylerle sınanmış, doğruluğu trilyonda bir hata payıyla saptanabilmiştir.
Çeşitli gezegenlerin Güneş çevresindeki eliptik yörüngelerinin büyük eksenleri, yörünge düzleminde yavaşça döner. Merkürün yörüngesinin yüzyıl başına 574 açı saniyelik dönüşünün 531 açı saniyelik bölümü, öbür gezegenlerin kütleçekimi etkisinden kaynaklanır. Geriye kalan 43 açı saniyelik dönme ise ancak genel görelilik kuramı ortaya çıktıktan sonra açıklanabilmiştir ve genel görelilik kuramının öngördüğü değerle kesin olarak uyuşmaktadır.
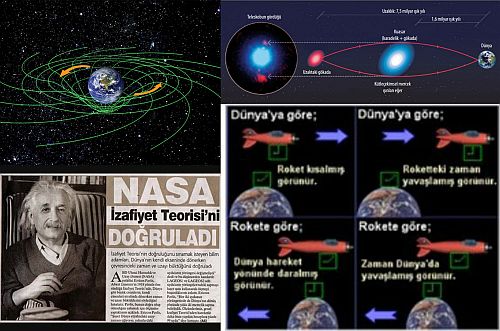
Genel görelilik, bir kütleçekimi alanı içinde bulunan ışık kaynağından yayılan ışığın dalgaboyunun büyüyeceğini, yani kırmızıya kayacağını öngörür. Bu etki, yüzeylerindeki kütleçekimi potansiyeli çok yüksek olan beyaz cüceler adı verilen yıldızlarda gözlenmiştir.
Uzay-zaman eğriliğinin bir sonucu, kütleçekimi alanlarından geçen ışık ışınlarının büküleceği ve yayılma hızlarının yavaşlaya- cağıdır. Kuramın yayımlanmasından birkaç yıl sonra tam Güneş tutulmasında Güneş diski yakınındaki bir yıldızın görüntüsünün gökte bulunması gereken yerden 1 açı saniyesinden daha küçük bir açıyla sapmış olduğunun saptanması da bu öngörüyü doğrulamaktadır.
GÖRELİLİK İLKELERİNİN UYGULAMALARI
Parçacık hızlandırıcılar
Çağdaş parçacık hızlandırıcıları, parçacıkların hızlarını ışık hızına çok yaklaştırırlar. Örneğin, milyarlarca elektronvoltluk enerjilerde çalışan elektron senkrotronlarında, yörüngedeki bir elektronun kütlesi, durgun kütlesinin 10 bin katma çıkabilir. Hızı ise ışık hızına çok yakın değerler alabilir. Bu nedenle, parçacık hızlandırıcılarının tasarımlarında görelilik etkilerinin göz önünde bulundurulması zorunludur.
Göreli parçacık fiziği
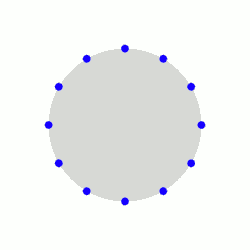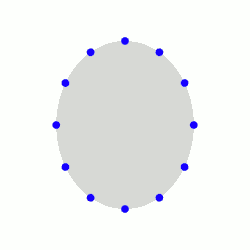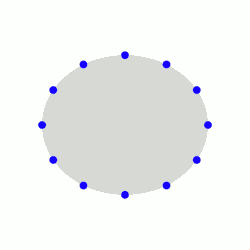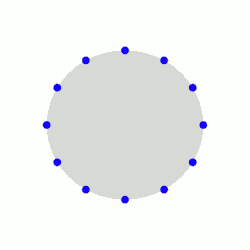
Kütleçekimsel dalga tarafından
etkilenen test parçacıklarının çemberi
Atomaltı parçacıkların fiziği, özel görelilik kuramının ilkelerine bağlıdır. Bu ilkelerin doğrudan uygulamalarına parçacıkların yaratılış, yok ediliş ve başka parçacıklara dönüşümlerinde rastlanır. Parçacık dönüşümleriyle ortaya çıkan enerji alışverişleri, özel görelüiğin kütle ile enerjinin eşdeğerliği ilkesi uyarınca ortaya çıkar. Bir başka deyişle, böyle dönüşümlerde parçacıkların toplam durgun kütlelerinde ortaya çıkan değişim ile toplam enerji değişimi birbirlerine E=mc2 bağıntısıyla bağlıdır; bu kural evrensel olarak doğrulanmıştır. Durgun kütlesi sıfır olan foton, ışık hızıyla hareket ettiğinden, toplam enerjisinin c2ye bölünmesiyle bulunan bir görelilik kütlesine sahiptir. Bu görelilik kütlesi bir foton ile bir parçacık etkileştiğinde fotonun doğrusal momentumunda gözlenen değişimden yola çıkılarak hesaplanabilmekte ve görelilik kuramı gene doğrulanmaktadır.
Göreli kozmoloji
Özellikle 1960lardan sonra, yeni buluşlar ve gözlem tekniklerinin gelişmesi sonucunda özel ve genel görelilik kuramlarının uygulanmasıyla evrenin yapısı ve geçmişi üzerindeki araştırmalar çok ilerlemiştir. En uzak astronomik cisimlerin ışıklarında gözlenen kırmızıya kayma olayı, genişleyen evrende bu cisimlerin bizden hızla uzaklaştıklarına işaret etmektedir. Eğer genişleme sabit hızla olmaktaysa, bu olayın 2xl010 yıl önce başlamış olması düşünülmektedir.
Mikrodalgalar ile kızılötesi ışınımların sınır bölgesine düşen frekanslarda her yönden gelen fon ışınımlarının bulunuşu, evrenin geçmişte olağanüstü yoğun ve sıcak olduğu dönemlerin varlığının kanıtı sayılmaktadır. Genel görelilik kuramı kuramsal kozmolojiye evrenin bir bütün olarak düz olması gerekmediği, büyük bir olasılıkla da düz olmadığı görüşünü getirmektedir. Evrenin çok büyük (kozmolojik) ölçekte homojen ve yönsemez (özellikleri her yerde ve her doğrultu boyunca özdeş) olduğu kabul edilse bile çeşitli olasılıklar ortaya çıkmaktadır. Evren uzaysal olarak bir açık evren olabilir (düz bir evren doğal olarak açık evrendir) ya da bir küre yüzeyi gibi kendi üstüne kapalı olabilir, bu durumda sınırları da yoktur. Benzer biçimde, evrenin, zaman içinde açık ya da kapalı olduğu düşünülebilir.
Zaman içinde kapalı bir evren tasavvur etmek epeyce zordur, çünkü böyle bir evrenin alışılagelmiş neden-sonuç kavramlarıyla uyuşmadığı söylenebilir. Ama bu kavramlar normal günlük yaşamdan elde edilmiş kavramlardır, milyarlarca yıl içeren bir zaman ölçeğinde geçerli olmayabilirler. Çeşitli kozmolojik modeller ortaya konmuş ve bunlar kuramsal olarak incelenmiştir, ama gözlem sonuçlarının bu modellerden herhangi birini doğruladığı söylenemez. Gözlemlerden elde edilen bilgiler, evrenin geçmişte bir ateştopu (olağanüstü yoğun ve sıcak madde) durumunda iken genleşerek oluştuğu görüşünü içeren modelleri destekleyici niteliktedir.
Son düzenleyen Safi; 16 Ocak 2017 18:54
Gerçekçi ol imkansızı iste...

 Genel Görelilik Kuramı
Genel Görelilik Kuramı