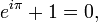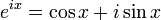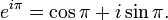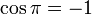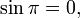Ziyaretçi
Euler Özdeşliği
Vikipedi, özgür ansiklopedi
Özdeşliğin Doğası
Euler özdeşliği birçok matematikçi tarafından göze hoş gelen bir denklem olarak tanımlanmaktadır. Denklem, aritmetik işlemlerden toplama, çarpma ve üs almayı içerir. Euler özdeşliği matematiğin beş temel sabitini de içerir:
Özdeşliğe İlişkin Düşünceler
Mathematical Intelligencer okurları tarafından yanıtlanan bir anket sonucuna göre Euler özdeşliği matematiğin en hoş kuramıdır. Physics World tarafından 2004 yılında yapılan bir diğer anket sonucuna göre ise Euler eşitliği Maxwell denklemleri ile birlikte "gelmiş geçmiş en büyük denklemler" olarak belirlenmiştir.
Paul Nahin'in Dr. Euler'in Enfes Formülü (2006) adlı kitabı Euler özdeşliğine adanmıştır. Dörtyüz sayfa uzunluğundaki bu kitap Euler özdeşliğinin "matematiksel güzelliğin zirvesine ulaştığı" kanısındadır.
Constance Reid, Euler özdeşliğinin "matematiğin en önemli formülü" olduğunu öne sürmüştür.
Gauss'un bu formülü ilk duyduğunda anlayamayan hiçbir öğrencinin birinci sınıf bir matematikçi olamayacağını söylediğine inanılmaktadır.
19. yüzyılın ünlü matematikçilerinden Benjamin Peirce bir dersinde özdeşliği kanıtladıktan sonra şunları söylemiştir:
Çıkarımı
gerçel sayısı için aşağıdaki eşitliği sağlamaktadır.
Euler özdeşliği aşağıda formülü verilen eşitliğin n = 2 durumunu sağlar.
Euler, formülünün e sayısını cos ve sin terimleriyle ilişkilendirdiğini birçok yerde belirtmiştir ancak Euler'in kendi adına atfedilen özdeşliği bulduğuna dair somut bir kanıt bulunmamaktadır. Bazı kaynaklar bu özdeşliğin Euler'in doğumundan önce kullanılmakta olduğunu öne sürmektedirler. (Durum böyleyse bu, Stigler adlandırma yasasına bir örnek oluşturabilir.) Bu nedenle, özdeşliğin Euler'e atfedilmesinin uygun olup olmadığı konusunda genel bir kabul yoktur.
Vikipedi, özgür ansiklopedi
Sponsorlu Bağlantılar
Matematiksel çözümlemede Euler özdeşliği olarak adlandırılan ve Leonhard Euler (bak. Leonhard Euler) tarafından bulunan eşitlik
dır. Burada,
-
 , doğal logaritma tabanı Euler sayısını,
, doğal logaritma tabanı Euler sayısını, 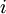 , karesi -1'e eşit olan karmaşık sayıyı,
, karesi -1'e eşit olan karmaşık sayıyı,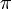 , bir çemberin çevre uzunluğunun çapına oranına eşit olan pi sayısını ifade eder.
, bir çemberin çevre uzunluğunun çapına oranına eşit olan pi sayısını ifade eder.
Özdeşliğin Doğası
Euler özdeşliği birçok matematikçi tarafından göze hoş gelen bir denklem olarak tanımlanmaktadır. Denklem, aritmetik işlemlerden toplama, çarpma ve üs almayı içerir. Euler özdeşliği matematiğin beş temel sabitini de içerir:
- 0 sayısı
- 1 sayısı
- Trigonometri, Öklit geometrisi ve matematiksel çözümlemenin vazgeçilmez unsurlarından pi sayısı
- Doğal logaritma tabanı olarak da adlandırılan e sayısı (bak. e sayısı ≈ 2.71828)
- Karmaşık sayıların temel birimi olan ve integral gibi birçok işleme izin veren i sayısı
Özdeşliğe İlişkin Düşünceler
Mathematical Intelligencer okurları tarafından yanıtlanan bir anket sonucuna göre Euler özdeşliği matematiğin en hoş kuramıdır. Physics World tarafından 2004 yılında yapılan bir diğer anket sonucuna göre ise Euler eşitliği Maxwell denklemleri ile birlikte "gelmiş geçmiş en büyük denklemler" olarak belirlenmiştir.
Paul Nahin'in Dr. Euler'in Enfes Formülü (2006) adlı kitabı Euler özdeşliğine adanmıştır. Dörtyüz sayfa uzunluğundaki bu kitap Euler özdeşliğinin "matematiksel güzelliğin zirvesine ulaştığı" kanısındadır.
Constance Reid, Euler özdeşliğinin "matematiğin en önemli formülü" olduğunu öne sürmüştür.
Gauss'un bu formülü ilk duyduğunda anlayamayan hiçbir öğrencinin birinci sınıf bir matematikçi olamayacağını söylediğine inanılmaktadır.
19. yüzyılın ünlü matematikçilerinden Benjamin Peirce bir dersinde özdeşliği kanıtladıktan sonra şunları söylemiştir:
"Bu özdeşlik ilk bakışta çelişkili gibi duruyor ancak bunu kanıtladıktan sonra gerçeğin ta kendisiyle karşı karşıya olduğumuzu görüyoruz."Stanfordlu matematik profesörü Keith Devlin, Euler özdeşliği hakkında şunları söylemiştir:
"Euler özdeşliği aşkın gerçek anlamını kavrayan bir Shakespeare sonatı ya da insanın ruhuna işleyen bir resim gibi varoluşun en derinlerine iniyor."
Çıkarımı
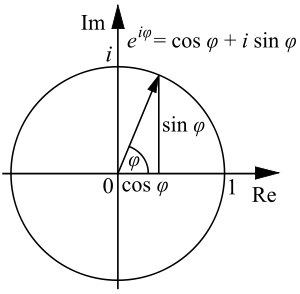
Özdeşlik, karmaşık çözümlemedeki Euler formülünün özel bir durumudur. Euler formülü her x
Euler özdeşliğinin rastgele bir açıya uygulanması
gerçel sayısı için aşağıdaki eşitliği sağlamaktadır.
eşitliği sağlanıyorsa
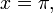
ifadesi elde edilir. Bunun nedeni
ve
eşitliklerinin sağlanmasıdır. Bunun ardından aşağıdaki eşitlik elde edilir.
ve bu eşitlik bizi Euler özdeşliğine götürür.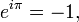
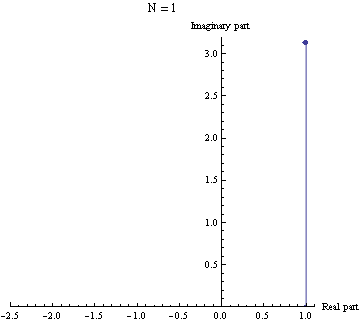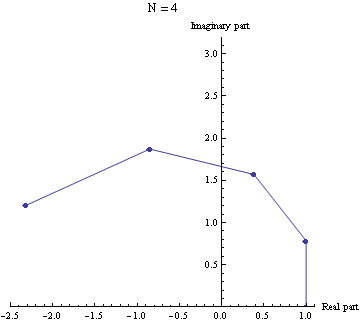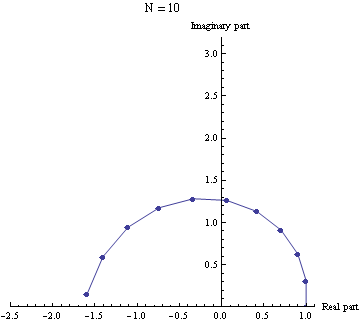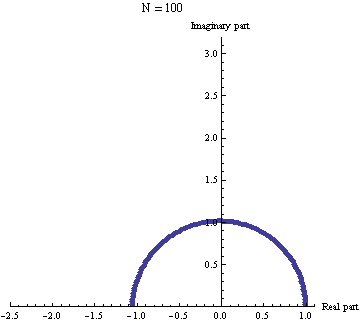
Genelleme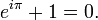
Euler özdeşliği aşağıda formülü verilen eşitliğin n = 2 durumunu sağlar.
Atıf Sorunu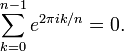
Euler, formülünün e sayısını cos ve sin terimleriyle ilişkilendirdiğini birçok yerde belirtmiştir ancak Euler'in kendi adına atfedilen özdeşliği bulduğuna dair somut bir kanıt bulunmamaktadır. Bazı kaynaklar bu özdeşliğin Euler'in doğumundan önce kullanılmakta olduğunu öne sürmektedirler. (Durum böyleyse bu, Stigler adlandırma yasasına bir örnek oluşturabilir.) Bu nedenle, özdeşliğin Euler'e atfedilmesinin uygun olup olmadığı konusunda genel bir kabul yoktur.

 Euler Özdeşliği
Euler Özdeşliği