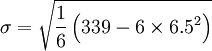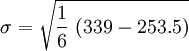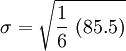Arama

Standart Sapma

Güncelleme: 6 Haziran 2013 Gösterim: 11.521 Cevap: 5

Cevap Yaz

ThinkerBeLL

VIP VIP Üye

25 Nisan 2010 Mesaj #1

VIP VIP Üye

Standart Sapma
MsXLabs.org & Vikipedi, özgür ansiklopedi

Sponsorlu Bağlantılar

Olasılık kuramı ve istatistik bilim dallarında, bir anakütle veya bir örneklem veya bir olasılık dağılımı veya bir rassal değişken için standart sapma, veri değerlerinin yayılımının özetlenmesi için kullanılan bir ölçüdür. Matematik notasyonunda genel olarak, bir anakütle veya bir rassal degişken veya bir olasılık dağılımı için standart sapma σ (eski Yunan harfi olan küçük sigma) ile ifade edilir; örneklem verileri için standart sapma için ise s veya s' (anakütle σ değeri için yansız kestirim) kullanılır.
Standart sapma varyansın kare köküdür. Daha matematiksel bir ifade ile standart sapma veri değerlerinin aritmetik ortalamadan farklarının karelerinin toplamının veri sayısı -1'e bölümünün kare köküdür, yani verilerin ortalamadan sapmalarının kareler ortalamasının karekökü olarak tanımlanır. Standart sapma kavramının yayılma ölçüsü olarak kullanılmasını anlamak için ölçüm birimine bakmak gerekir. Diğer yayılma ölçüsü olan varyans verilerin ortalamadan farklarının karelerinin ortalaması olarak tanımlanır. Böylece varyans ölçüsü için veri birimlerinin karesi alınması gerekir ve varyansın birimi veri biriminin karesidir. Bu durum pratikte istenmeyen sonuçlar yaratabilir (Örneğin veriler birimi kilogram ise varyans birimi kilogram kare olur). Bundan kaçınmak icin standart sapma için varyansın kare kökü alınarak standart sapma birim veri birimi olması sağlanır ve verinin yayılımı böylece veri birimleri ile ölçülür.
Örneğin: Bir basit anakütle için kilogram birimi ile veri (4, 8, 12) olsun. Aritmetik ortalama 8 olur ve verilerin ortalamadan sapmaları (−4, 0 , 4) olur. Kare toplamlarının ortalaması olan varyans

olur ve kilogram kare birimi ile verilir. Standart sapma 16'nın karekökü olup 4 değerdedir ve kilogram birimi ile ölçülür.
Standart sapma genel olarak niceliksel ölçekli sayılar için en çok kullanılan verilerin ortalamaya göre yayılmasını gösteren bir istatiksel ölçüdür. Eğer bir çok veri ortalamaya yakın ise, standart sapma değeri küçüktür; eğer birçok veri ortalamadan uzakta yayılmışlarsa standart sapma değeri büyük olur. Eğer bütün veri değerleri tıpatıp ayni ise standart sapma değeri sıfırdır.

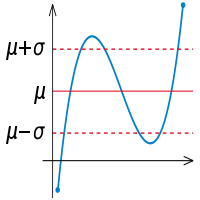
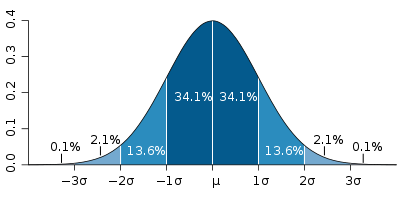
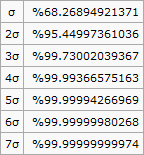
Mavi olarak gösterilen bir rassal değişken dağılımı için standart sapma değeri σ rassal değişken değerlerinin ortalama μ değeri etrafında yayılmasını gösterir.

Konu Başlıkları

Tanımlama ve hesaplama
- 1.1 Rassal değişken için standart sapma
- 1.2 Anakütle standart sapma değerinin örneklem standart sapma kullanılarak kestirimi
- 1.3 Bir sürekli rassal değişken için standart sapma
Açıklama ve uygulama
- 3.1 Normal dağılım gösteren veriler için kurallar
- 3.2 Çebişev'in eşitsizliği
Standart sapma ve ortalama arasındaki ilişki
Örnekler

BEĞEN Paylaş Paylaş

Bu mesajı 1 üye beğendi.

Tanrı varsa eğer, ruhumu kutsasın... Ruhum varsa eğer!

Cevapla

ThinkerBeLL

VIP VIP Üye

25 Nisan 2010 Mesaj #2

VIP VIP Üye

Tanımlama ve Hesaplama

Sponsorlu Bağlantılar

1. Rassal değişken için standart sapma
Bir rassal değişken olan X icin standart sapma şöyle tanımlanır:

Burada E(X) X için beklenen değer yani ortalama ve Var(X) X için varyans değeridir.
Her rassal değişken dağılım tipi için bir standart değer var olması gerekli değildir. Çünkü bazı dağılımlar için beklenen değer bulunamaz. Örneğin, Cauchy dağılımı gösteren bir rassal değişken X için bir standart sapma yoktur; çünkü E(X) tanımlanamaz.
Eğer bir rassal değişken X (reel sayılar olan) Ad: 5813731a2181538dcc186610eddec356.png
Gösterim: 561
Boyut: 326 Byte

Ad: 5813731a2181538dcc186610eddec356.png
Gösterim: 561
Boyut: 326 Byte

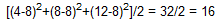
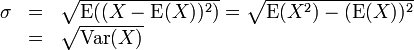
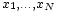değerlerini eşit olasılıkla alırsa, o rassal değişken için standart sapma şöyle hesaplanır:
Önce, X için ortalama Ad: 34fd2436571a41ac9080dd4e238e72a5.png
Gösterim: 549
Boyut: 195 Byte

Ad: 34fd2436571a41ac9080dd4e238e72a5.png
Gösterim: 549
Boyut: 195 Byte

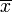, şu toplam olarak tanımlanır: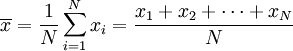

Burada N alınan örneklem büyüklüğü sayısıdır.
Sonra, standart sapma ifadesi şöyle basitleştirilir:

Yani, bir aralıklı tekdüze dağılım gösteren rassal değişken X icin standart sapma şöyle hesaplanır:

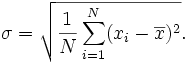
Her xi değeri icin xi le ortalama değer olan arasında olan farklar 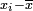olarak bulunur.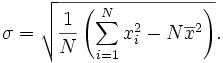
Bu farkların kareleri hesaplanır.
Bu farkların karelerinin ortalaması bulunur. Bu değer varyans, yani σ², olur.
Bu varyans değerinin kare kökü alınır.

Ancak hesaplari elle veya el hesap makinasi ile yapmak için genellikle daha uygun bir formül kullanılır:

Bu iki formülün birbire eşitliği biraz cebir kullanılarak gösterilebilir:

2. Anakütle standart sapma değerinin örneklem standart sapma kullanılarak kestirimi
Pratik hayatta, her bir anakütle elemanın ölçülmesini gerektiren bir anakütle standart sapma değeri bulmak, bazı çok nadir haller dışında (örnegin standart hale getirilmiş mekanik test etme), hiç realistik değildir. Nerede ise her halde, anakütleden bir rasgele örneklem alınır ve bu örneklemden anakütle standart sapması için bir kestirim değer bulunur. Bu kestirim, çok kere örneklem standart sapmasını anakütle standard sapmasının aynı olan bir formülü kullanmak suretiyle yapılır:

Burada

Ad: 722bfdb882d00ea9cc84ba9249b99d2f.png
Gösterim: 507
Boyut: 404 Byte

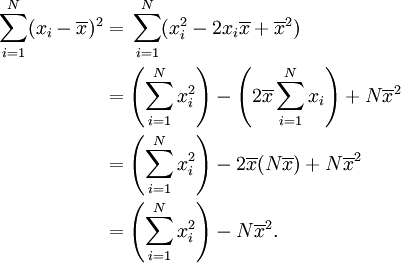
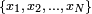örneklem değerleri ve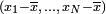 Ad: 8ca96727b4c0d19c76963a3d1b9488bd.png
Gösterim: 558
Boyut: 150 Byte

örneklem ortalamasıdır. Bölen değer olan N − 1

vektörü içinde bulunan serbestik derecesi olur.
Bu belki bir bakıma uygundur; çünkü eğer bir anakütle varyansının kavramsal olarak var olduğu biliniyorsa ve örneklem için anakütleden her eleman çekiminden sonra bu eleman geri konulursa, bilinmaktedir ki örneklem varyansı (yani s²) anakütle varyansı (yani σ²) için bir yansız kestirim olur. Ancak bu standart sapmalar için doğru değildir; yani yukaridaki gibi bulunan örneklem standart sapması (s) anakütle standart sapması (σ) için yansız kestirim değeri değildir ve s ile anakütle standart sapması biraz daha küçükce tahmin edilir. Eğer rassal değişken normal dağılım gösteriyorsa, bu yansız olan kestirim pratikte çok kolay olmayan bir dönüşüm ile elde edilebilmektedir. Ayrıca zaten bir kestirim için yansız olmak karekteri her zaman çok istenir bir özellik değildir.
Çok kullanılan diğer bir kestrim ise benzer bir ifade ile şöyle verilir:

olur. Eğer anakütle normal dağılım gösteriyorsa, bu şekildeki kestirim yansız kestirimden her zaman biraz daha küçük ortalama hata karesi gösterir ve bu nedenle normal için maksimum olabilirlik kestirimi olur.

3. Bir sürekli rassal değişken için standart sapma
Sürekli olasılık dağılımları için genellikle standard sapma değerinin dağılıma özel olan parametreleri kullanılarak hesaplanması için förmül vardır. Genel olarak ise, p(x) olasılık yoğunluk fonksiyonu olan bir sürekli rassal değişken olan X için standart sapma şöyle verilir:

Burada

BEĞEN Paylaş Paylaş

Bu mesajı 1 üye beğendi.

Tanrı varsa eğer, ruhumu kutsasın... Ruhum varsa eğer!

Cevapla

ThinkerBeLL

VIP VIP Üye

26 Nisan 2010 Mesaj #3

VIP VIP Üye

Açıklama ve Uygulama

Belli bir seri sayı için standart sapma değerini bilmek ve bu kavramı anlamak demek bir ortalama etrafında bu serinin ne kadar yayılım gösterdiğini anlamaktır. Standart sapmanın büyük olması veri noktalarının ortalamadan daha uzak yayıldıklarını; küçük bir standart sapma ise ortalama etrafında daha çok yakın gruplaştıklarını gösterir.
Standart sapma belirsizliğin bir ölçüsü olarak hizmet edebilir. Fiziksel bilimlerde, tekrar tekrar yapılan deneyler ve deneylerde alınan ölçüler ise gösterilen standart sapma oldusu bu deneyin ölçülmesindeki kesinlik ve doğruluğunu gösterir. Ölçümlerin teoriye dayanan bir tahmin ile karşılaştırıp birbirine uygunluk gösterip göstermediğine karar vermede ölçümlerin standart sapması önemli rol oynar. Eğer ölçümlerin standart sapması teorik tahminden çok daha uzaksa, sınanan teorinin değiştirilmesi gerekir. İşte bu uzaklık standart sapmalarla belirlenir.
Finansmanda, standart sapma verilmiş bir menkul (hisse senedi, tahvil, emlak v.b) için rizikonun veya bir menkuller portföyü için rizikoları temsil eder. Bir yatırım portföyünün etkin olarak idare edilmesini tayin eden en önemli faktörlerden birisi rizikodur. Çünkü her tek bir menkulün veya bir menkuller portföyünün getirisindeki mümkün yayılımını riziko tanımlar ve rizikonun standart sapma ile tanımlanması ise yatırım kararları için bir matematiksel temel sağlar. En geniş kavramla, yatırım rizikosu arttıkça menkul veya menkuller portföyünün beklenen getirisi da artış gösterir. Buna neden yatırımcıların menkul getirileri icin riziko primlerini artırmaları olarak açıklanır. Diğer bir deyişle, eğer bir yatırım daha yüksek riziko seviyesi taşıyorsa, yatırımcılar o yatırımdan daha yüksek bir getiri beklemeleri gereklidir.
Uzunca bir zaman içinde herhangi bir menkul için yıllık getirilerinin ortalamasını bulmakla o menkul için beklenen getiri değerini vermektedir. Her yıl için elde edilen getiriden bu beklenen getiri farkı bulunursa buna finansmancılar ve muhasebeciler tarafından varyans adı verilir (Dikkat edilirse bu istatistiksel varyans kavramından farklıdır). Her bir yıl için varyansın karesini bulmak ve bu varyans karelerinin ortalamasının karekökü o menkulün standart sapmasını yani rizikosunu gösterir. İşte bu rizikolar yani varyanslarin karelerinin toplamının ortalamasının karekökü, standart sapmadır ve rizikoyu ölçer. Menkullerin karşılaştırılımı için temel çalışma işte bu ölçü ile yapılır.
Standart sapmalar için pratik uygulamalar daha değişik alanlarda da verilebilir; fakat burada bu ufak sayıda uygulamalar bile standart sapmanın uygun bir şekilde önemini ortaya çıkartmaktadır.

1. Normal dağılım gösteren veriler için kurallar

Koyu mavi ortalamadan bir standart sapmadan daha düşük değerleri gösterir. Normal dağılım için bu %68,27 olur; (orta ile koyu mavi) ortalamadan iki standart sapma için %95,45; (açık, orta ve koyu mavi için) ortalamadan üç standart sapma %99,73 olur.

Pratikte, çok zaman verilerin yaklaşık olarak bir normal dağılım gösteren anakütleden geldiği varsayılır. Bu varsayıma neden olarak merkezsel limit teoreminin geçerliliği iddiası olur. Merkezsel limit teoremine göre birçok birbirinden bağımsız ve hepsi aynı dağılım gösteren rassal değişkenlerin toplamı limitte bir normal dağılıma göre eğilim gösterirler. Eğer bu varsayim geçerli ise, değerler yaklaşık %68,27 olasılıkla ortalamadan eksi ve artı bir standart sapma noktalarının arasında bulunur; ortalamadan artı ve eksi 2 standart sapma noktaları arasında %95,45 olasılıkla ve ortalamadan artı ve eksi 3 standart sapma noktaları arasında %99,73 olasılıkla bulunur. Bu 68-95-99.7 kuralı veya bir emprik kural olarak bilinir.
Güvenlik aralıkları şöyle gösterilebilir:

Çebişev'in eşitsizliği
Yakınlık standart sapma birimlerinde ifade edilirse, herhangi bir veri serisi için, Çebişev'in eşitsizliği ile isbat edilmiştir ki veri değerlerin çok büyük bir çoğunluğu ortalama değere yakındır. Çebişev'in eşitsizliği sadece normal dağılım gösteren seriler için değil, bütün rasgele dağılım gösteren veri serileri için geçerlidir. Buna göre, şu zayıf sınırlar ve bu sınırlar içinde bulunan veri yüzdesi şöyle verilebilir:

Ortalamadan √2 standart sapma uzaklıkları arasında değerlerin en aşağı %50'si bulunur.
Ortalamadan 2 standart sapma uzaklıkları arasında değerlerin en aşağı %75'i bulunur.
Ortalamadan 3 standart sapma uzaklıkları arasında değerlerin en aşağı %89'u bulunur.
Ortalamadan 4 standart sapma uzaklıkları arasında değerlerin en aşağı %94'ü bulunur.
Ortalamadan 5 standart sapma uzaklıkları arasında değerlerin en aşağı %96'sı bulunur.
Ortalamadan 6 standart sapma uzaklıkları arasında değerlerin en aşağı %97'si bulunur.
Ortalamadan 7 standart sapma uzaklıkları arasında değerlerin en aşağı %98'i bulunur.

Genel olarak:

Ortalamadan k standart sapma uzaklıkları arasında değerlerin en aşağı %(1 − 1/k²) × 100'si bulunur.

BEĞEN Paylaş Paylaş

Bu mesajı 1 üye beğendi.

Tanrı varsa eğer, ruhumu kutsasın... Ruhum varsa eğer!

Cevapla

ThinkerBeLL

VIP VIP Üye

26 Nisan 2010 Mesaj #4

VIP VIP Üye

Standart Sapma ve Ortalama arasındaki ilişki

Çok kere bir veri serisinin özetlenmesinde ortalama ve standart sapma birlikte bildirilmektedir. Bir anlamda, eğer ortalama verilerinin merkezi olarak kullanılan ölçü ise, standart sapma veri yayılımının doğal ölçüsüdür. Buna neden ortalama noktasıdan standart sapmanın, verinin herhangi bir noktasıdan standarize edilmiş sapmadan daha küçük olduğudur. Bu matematiksel ifade ile şöyle gosterilebilir:
x1, ..., xn reel sayılar olsun ve şu fonksiyon tanımlansın:

Ya birinci türev alınıp sıfıra eşit yaparak veya daha kolay bir cebirsel yol olan kare tamamlaması kullanarak σ(r)'nın tek ve sadece tek bir minimum noktasının aritmetik ortalama olduğu; yani

gösterilebilir.
Standart sapma ile ortalama arasındaki diğer bir ilişki ise yayılım özelliğine dayanan veri karşılaştırılmaları için kullanılan varyasyon katsayısıdır. Bir veri serisi için varyasyon katsayısı standart sapma ile ortalama arasındaki orandır. Böylece, standart sapma (ve ortalama) veri birimleri ile boyutlu iken (örnegin veri TL ile ise standart sapma ve ortalama TL birimlerindedir); varyasyon katsayısı boyutsuz sırf bir sayıdır. Bu nedenle değişik birimlerde olan verilerin yayılımlarının karşılaştırılması için kullanılabilir.

BEĞEN Paylaş Paylaş

Bu mesajı 1 üye beğendi.

Tanrı varsa eğer, ruhumu kutsasın... Ruhum varsa eğer!

Cevapla

ThinkerBeLL

VIP VIP Üye

26 Nisan 2010 Mesaj #5

VIP VIP Üye

Örnekler

Burada önce çok ufak bir anakütle veri serisi için standart sapma hesaplaması gösterilmektedir. Bu seri bir inşaat firmasının yabancılara yaptığı aylık daire satış sayılarını göstermektedir ve veri serisi şudur: {5, 2, 11, 12, 3, 6}

1. Önce bir aritmetik ortalama Ad: 34fd2436571a41ac9080dd4e238e72a5.png
Gösterim: 480
Boyut: 195 Byte

Ad: 34fd2436571a41ac9080dd4e238e72a5.png
Gösterim: 480
Boyut: 195 Byte

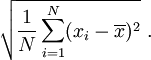
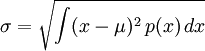
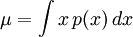
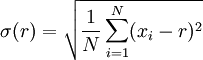
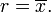
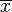şöyle hesaplanır: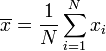

Burada i her veriye verilen sıra numarasıdır, yani i=1, 2, 3, ..., 6.
Yani;

x1=5
x2=2
x3=11
x4=12
x5=3
x6=6

Bu halde N = 6 olup veri büyüklüğü veya anakütle hacmidir.

N yerine 6

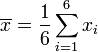
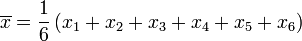
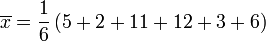
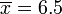> Bu aritmetik ortalamadır.

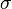2. Standart sapma $5b33f39cef9df8c1d0386c99deb5c8d9$ değerini bulma: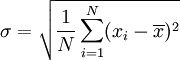

N yerine 6

yerine 6.5

Ad: 1f801da1e662be550e9f2a43ea4bfd83.jpg
Gösterim: 469
Boyut: 6.0 KB

Ad: 08f56b08908ca40b548cc3bf831e961e.png
Gösterim: 465
Boyut: 1.8 KB

Ad: c6e40a74f768d1a408783abf3bd79dba.png
Gösterim: 459
Boyut: 1.4 KB

Ad: 193332656f01aebf594b24dac6f103eb.png
Gösterim: 450
Boyut: 825 Byte

Ad: 5df684703ccbcbdee0d1e6485e02b782.png
Gösterim: 498
Boyut: 546 Byte

Ad: 60ea35471152805bd7a9ed34f7ef5cea.png
Gösterim: 476
Boyut: 391 Byte

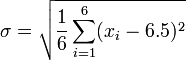
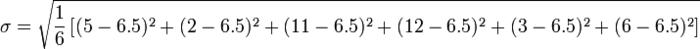
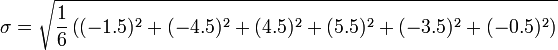
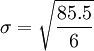
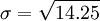
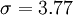> Bu standart sapma değeri olur.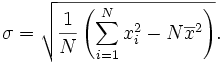

Bu sonucun dikkati çekecek bir yanı verilerin tam sayı olmasına rağmen standart sapmanın (ve ayni şekilde aritmetik ortalamanın) kesirli olmasıdır.
Bu hesaplamayı daha kolaylaştırmak için şu formül kullanılabilir:

1. Önce bir aritmetik ortalama Ad: 34fd2436571a41ac9080dd4e238e72a5.png
Gösterim: 480
Boyut: 195 Byte

hesaplanır:

> Bu aritmetik ortalamadır.

2. Sonra toplam kareler bulunur:

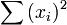= 5² + 2² + 11² + 12² + 3² + 6²
= 25+4+121+144+9+36
= 339

3. Bunlar formüle konulur:
Yani Ad: 1ee3aaddc3c0db07fe94da37f154d9a5.png
Gösterim: 466
Boyut: 526 Byte

= 339,

Ad: 3a2cb8eab59c18968c2aa5976608b6ec.png
Gösterim: 462
Boyut: 346 Byte

, N = 6 formüle girer:

> Bu standart sapma değeridir.

BEĞEN Paylaş Paylaş

Bu mesajı 1 üye beğendi.

Tanrı varsa eğer, ruhumu kutsasın... Ruhum varsa eğer!

Cevapla

Efulim

VIP VIP Üye

6 Haziran 2013 Mesaj #6

VIP VIP Üye

Standart Sapma
MsXLabs.org & Morpa Genel Kültür Ansiklopedisi

İstatistikte, varyansın pozitif karekökü ya da bir başka deyişle, gözlemlerin her birinin, tüm gözlemlerin aritmetik ortalamasından sapma miktarlarının karelerinin aritmetik ortalaması. Formülü: dir. Bu formülde ? standart sapma, µ ortalama, xi de i'ninci gözlemdir. Standart sapma, bir dağılımın, ortalaması etrafındaki yayılmanın ölçüsüdür. Örneğin normal bir dağılımda, popülasyonun yaklaşık %63,8'i ortalamadan bir standart sapma kadar uzaklaşır.

BEĞEN Paylaş Paylaş

Sen sadece aynasin...

Cevapla

Cevap Yaz