1 . Bir ucundan öbür ucuna kadar yönü değişmeyen, eğri ve çarpık karşıtı.
"Doğru haber."- .
3 . Akla, mantığa, gerçeğe veya kurala uygun:
"Bunları sana şimdiden söylemek daha doğrudur."- A. Gündüz.
4 . isim Gerçek, hakikat:
"Söyleyin doğrusunu, siz insanoğlunun ahlaklı olabileceğine inanmıyorsunuz."- N. Ataç.
5 . isim, matematik İki nokta arasındaki en kısa çizgi:
"İki noktadan yalnız bir doğru geçebilir."- .
6 . zarf Yanlışsız, eksiksiz bir biçimde:
"Doğru söylüyorsun Ali, doğru söylüyorsun ama kazın ayağı öyle değil."- O. Kemal
7 . zarf Hiçbir yöne sapmadan, dosdoğru, doğruca:
"Doğru oraya gitmiş olsaydınız herhâlde uygun olurdu."- S. F. Abasıyanık. 8 . zarf Yakın, yakınlarında:
"Şafağa doğru otomobil sesi duyuldu."- F. R. Atay. 9 . edat Karşı yönünce:
"Börekçi fırınının karşısındaki dört köşe taşlar döşeli, iki yanı ağaçlı yoldan çarşıya doğru yürüyordu."- Y. Atılgan. 10 . mecaz Yasa, yöntem ve ahlaka bağlı, dürüst, namuslu.
Doğru (matematik)
Vikipedi, özgür ansiklopedi

Üç doğru
Doğru, Matematikte mantıksal bir değer. Matematikte ne olduğu belli olmayan (tanımsız) değerlerden biridir. Hakkında doğru veya doğru değil diye değer yükleyebileceğimiz cümlelerden mümkün olduğu kadar azına "doğru" değeri veririz. Sonra mantıki olarak yeni cümlelerin değerlerini araştırırız. Ayrıca geometride ifadesi aynı doğrultuda olan ve her iki yönden de sonsuza kadar giden noktalar kümesi diye de tanımlanır. Bir doğru üzerinde en az 2 nokta, dışında da en az 1 nokta mevcuttur.
Tanım
Matematikte doğrunun değişik ifadeleri vardır:
Bir noktalar kümsidir.
Cetvel yardımıyle çizilen çizgi, iki nokta arasındaki gergin bir ip doğruyu belirtir.
Farklı 2 noktadan bir ve yalnız 1 doğru geçer.
Farklı 2 nokta bir ve yalnız 1 doğru belirtir.
Farklı 2 düzlem en fazla 1 doğruda kesişir.
Örnekler
 burada:
burada:m doğrunun eğimi.b doğrunun düşey eksenle kesişme noktası.x y fonksiyonunun bağımsız değişken. Üç boyutluda, bir doğru genellikle parametrik eşitlikler olarak ifade edilir:


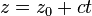 burada:
burada:x, y ve z, tden bağımsız fonksiyonlardır.x0, y0, ve z0 herbiri kendi değişken olan birincil değerlerdi.a, b, ve c doğrunun eğimine bağlıdırlar, böylece vektör (a, b, c) doğruya paraleldirler.
Geleneksel tanım
R2de, tüm doğrular L ile tanımlanır.

Özellikleri


 Doğru nedir?
Doğru nedir?
