Ziyaretçi
Özel Görelilik Kuramı

görelilik
Sponsorlu Bağlantılar
Fizikte görelilik kuramlarından birincisi, Albert Einsteinın 1905te geliştirdiği özel görelilik kuramıdır. İkincisi ise, gene Einsteinm 1916da öne sürdüğü genel görelilik kuramıdır. Özel görelilik kuramı, elektriksel ve magnetik olayları ve bunların uzay ve zaman içinde yayılmalarını inceler. Genel görelilik kuramı ise kütleçekimi sorununu konu edinmiştir. Her iki kuram da günlük yaşamda yararlanılan uzay ve zaman yaklaşımından çok farklı yaklaşımlar üzerine kurulmuştur. Göreli uzay ve zaman kavramları, atomdan evrene kadar bütün fiziksel olayların çağdaş yorumlarının ayrılmaz bir parçası olmuştur.
ÖZEL GÖRELİLİK KURAMI
Tarihsel gelişim.
Klasik fiziği sistemleştiren Sir Isaac Newtona göre bir cisim bir başka cisim üzerine bir etki yaptığında, bu etki, o cismin hareket durumunda bir değişikliğe yol açar. Yani bir parçacığın bir başkası üzerine uyguladığı kuvvet, ikinci parçacığın ya hızının büyüklüğünü ya hareketinin doğrultusunu ya da her ikisini birden değiştirir. Hiçbir dış etki altında olmayan bir parçacık ise doğrultusu değişmeyen ve hızı sabit bir hareket yapar. Bir parçacığın hareketi ancak belirli bir referans sistemine göre tanımlanabileceğinden, Newtonun eylemsizlik yasası, bir dış etkiye uğramayan parçacıkların değişmeyen bir doğrultuda ve sabit hızla hareket ettikleri (eylemsiz referans sistemi olarak adlandırılan) referans sistemleri vardır, biçiminde de ifade edilebilir. Klasik mekaniğin bütün yasaları böyle referans sistemlerinde geçerlidir.
Newtona göre, herhangi iki eylemsiz referans sistemi birbirlerine göre doğrusal, düzgün ve dönmeksizin (doğrultusu değişmeyen ve sabit hızla) hareket eder ve iki sistemdeki saatler (yeryüzünde iki farklı saat diliminde bulunan saatler gibi aralarında sabit bir fark bulunsa da) aynı hızla işler. Bu nedenle, herhangi iki olgu, bu eylemsiz sistemlerden birindeki gözlemci tarafından eşzamanlı olarak gözlenirse, tüm öbür gözlemcilere de eşzamanlı görünecektir. Zamanın ve zaman belirlemelerinin bu evrenselliği, genellikle zamanın mutlak karakteri olarak adlandırılmıştır.
Fiziksel evrenin yapı taşlarının parçacıklar olduğu ve boş uzayda birbirleriyle etkileşen parçacık sistemlerinin Nevvtonun öngördüğü ilkelere uyduğu düşünüldüğü sürece, klasik fizikteki uzay ve zaman kavramlarının geçerliğinden kuşkulanmak için bir neden bulunmamaktaydı. Ama 19. yüzyılda elektriksel ve magnetik olayları inceleyen Hans Christian Orsted ve Michael Faraday m buluşları ile James Clerk Maxwellin kuramsal çalışmaları, bu doğa görüşünün yeniden sorgulanmasını zorunlu kıldı.
Elektrik yüklü cisimler ve mıknatıslar, aralarında çok büyük uzaklıklar bulunduğunda birbirlerini neredeyse hiç etkilemezler; ama görece yakın olduklarında uzayda saniyede yaklaşık 300.000 km hızla yayılan bir elektromagnetik alan aracılığıyla etkileşirler. İçinde bildiğimiz hiçbir madde bulunmayan bölgelerde elektrik ve magnetik alanları neyin taşıdığı, elektromagnetik alan kuramını öne süren Maxwell ile laboratuvarda bu dalgaları elde eden Heinrich Hertzin başlıca sorunu olmuştu. O güne değin, sonlu hızla yayıldığı bilinen alan ve dalgalar, su dalgaları gibi yüzey dalgaları ile deprem şokları gibi düşük frekanslı dalgalar ve ses duyusu olarak algılanan dalgalardı. Maxwell, elektromagnetik dalgaların uzaydaki gizemli taşıyıcısına esir (eter) adını verdi. Elektromagnetik dalgaların bilinen özelliklerini taşıdığı düşünülen esir kavramı, bu taşıyıcının varlığının deneysel olarak saptanması sorununu ortaya çıkardı. 1887de iki ABDli fizikçi, Albert Abraham Michelson ile Edward Willams Morley, yeryüzü üzerinde esirin hızını ölçmek için bir deney tasarladılar. Yerin evrenin ekseni olmadığı varsayımı geçerli ise, farklı doğrultularda yol alan ışık ışınlarının (Yere ve laboratuvar aygıtlarına göre) gözlenen hızlan arasında, Yerin esire göre hareketi nedeniyle küçük farkların ortaya çıkması gerekiyordu. Eğer bir ışık demetinin ayna yardımıyla ileri ve geri yönlerde yol alması sağlanırsa, belli bir konum için toplam gidiş geliş süresi ölçülerek demetin hızı bulunabilir. Hızın mutlak değeriyle değil de iki ayrı yoldaki hızların farklarıyla ilgileniliyorsa, birbirine dikey iki yoldaki gidiş geliş süreleri karşılaştırılabilir. Michelson ve Morley, saat kullanmaktan kaçınmak için, dikey yönlerde yol alan ışık demetlerinin birbirleri ile optik girişim yapmalarını sağlayarak bu iki demetin gidiş geliş sürelerini dalga- boylannın sayısı cinsinden karşılaştırdılar. Bu çok duyarlıklı deney, sürekli geliştirilen tekniklerle birçok kez yinelendi. Elde edilen birbiriyle uyumlu sonuçlar, ışık hızının, yılın hangi gün ve saatinde ölçüldüğüne ya da laboratuvarın konumuna bakmaksızın her doğrultuda aynı olduğunu gösterdi.
Özel görelilik kuramı, bu deneysel bulgudan kaynaklandı: Yeryüzünde ki gözlemci, Yerin esir içindeki hareketini saptayamadı- ğına göre, hareket durumu ne olursa olsun herhangi bir gözlemci için ışığın her doğrultudaki hızı aynı olmalıydı.
Uzayın ve zamanın göreliliği. İrlandalI fizikçi George Francis FitzGerald ve HollandalI fizikçi Hendrik Antoon Lorentz, Michelson-Morley deneyinin sonuçlarına yeni bir yorum getirdiler: Esir içinde hareket eden bir cismin, harekete dikey doğrultulardaki boyutları değişmeden kalmak üzere, hareket doğrultusundaki boyu kısalırsa, deney sonuçları ile esir kavramı uzlaştırıla- bilirdi. Cismin esire göre hızı v ve ışığın hızı c ile gösterilirse, kısalmayı veren oran
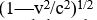 olur. Alışılmış hızlar, ışık hızından çok küçük olduğundan
olur. Alışılmış hızlar, ışık hızından çok küçük olduğundan 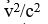 pratikte sıfırdır; kısalma gözlenemez. Ama v hızı, ışık hızına yaklaştığında bu oran önem kazanır. Örneğin, ışık hızının yaklaşık yüzde 87si kadar bir hızla hareket eden bir tismin boyu, durgun boyunun yansına inmiş görünür.
pratikte sıfırdır; kısalma gözlenemez. Ama v hızı, ışık hızına yaklaştığında bu oran önem kazanır. Örneğin, ışık hızının yaklaşık yüzde 87si kadar bir hızla hareket eden bir tismin boyu, durgun boyunun yansına inmiş görünür.Lorentz ayrıca, esirde hareket eden saatlerin, durgun saatlere göre, gene
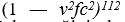 oranında yavaşladıklannın gözleneceğini de öne sürmüştür. Böylece esir içinde hareket eden tüm cetveller ve saatler, yapıldıkları malzemeden ve tasarımlarından bağımsız olarak sistematik değişikliklere uğrarlar. Bu nedenle kuramsal çözümlemeler yapılırken görünür ve gerçek uzay ve zaman ölçümleri arasında ayrım gözetilmelidir. Aynca gerçek zaman ve boyutların herhangi bir deneysel işlemle bülunamayacağı da göz önünde tutulmalıdır.
oranında yavaşladıklannın gözleneceğini de öne sürmüştür. Böylece esir içinde hareket eden tüm cetveller ve saatler, yapıldıkları malzemeden ve tasarımlarından bağımsız olarak sistematik değişikliklere uğrarlar. Bu nedenle kuramsal çözümlemeler yapılırken görünür ve gerçek uzay ve zaman ölçümleri arasında ayrım gözetilmelidir. Aynca gerçek zaman ve boyutların herhangi bir deneysel işlemle bülunamayacağı da göz önünde tutulmalıdır.Kavramsal açıdan tatmin edici olmayan bu durum 1905te Albert Einstein tarafından çözüme kavuşturuldu. Einstein farklı hareketler yapan gözlemciler arasındaki bütün karşılaştırmalarda anahtar kavramın evrensel (mutlak) eşzamanlılık kavramı olduğunu gördü. Bu, bir gözlemciye eşzamanlı görünen iki olgunun başka bütün gözlemciler için de eşzamanlı olarak algılanacağı anlamına gelir. Çok uzaktaki olguların anında gözlenebileceği kabul edilirse, bu, çok yalın bir önermedir. Ama gerçekte ışıktan ya da başka elektromagnetik ışınımlardan daha hızlı bir haber ulaştırma yöntemi bilinmemektedir. Yeryüzündeki bir gözlemcinin göğün farklı bölgelerindeki iki süpernovayı gözlediğini düşünelim. Yalnızca gökte görülmeleri sonucunda bu iki süpernovanın eşzamanlı patlayıp patlamadıkları söylenemez; gözlemciye göre uzaklıklarının da bilinmesi gerekir. Gökcisimleri binlerce ışık yılı uzaklıkta bulunabileceklerinden, süpernovalardan birinin öbüründen çok önce patlamış olması ve yola çıkardığı ışınların binlerce yıl geçtikten sonra öbürünün ışığı ile eşzamanlı olarak gözlemciye ulaşması çok olasıdır. Dolayısıyla bir gözlemci için iki olay eşzamanlı gözükürken, farklı hızlarda hareket eden gözlemciler için bu iki olay eşzamanlı gözükmeyebilir. Demek ki eşzamanlılığın göreli olduğu göz önünde tutulmalıdır.
Bu kuramsal çıkarsama, Fitz Gerald ve Lorentzin bulgularının yeniden yorurrtlan masına yol açtı. Birbirlerine göre hareketli olan eylemsiz referans sistemlerindeki gözlemcilerin, zaman aralıkları ve uzaklıklar için yaptıkları belirlemeler, sistematik biçimde uyuşmazlık içinde olacaktır. Gözlemcilerden hangisinin doğru, hangisinin yanlış olduğu da söylenemez. Gerçekten de iki gözlemci saatlerini karşılaştırırlarsa, her biri kendi saatinin ötekinin saatinden daha hızlı işlediğini görecektir. Benzer olarak öbür gözlemcinin cetvelinin boyunu da (hareket doğrultusunda olmak üzere) kısalmış bulacaktır.
Özel görelilik kuramının birinci postulası, esirin varlığının ortaya çıkarılamayacağıdır. İkinci postula, hareketli olsun ya da olmasın tüm gözlemcilere göre ışık hızının sabit kalacağıdır. Herhangi bir deneyle esirin varlığı ortaya çıkarılamayacağından, salt elektromagnetik dalgaların taşıyıcısı görevini yüklenmek üzere ortaya atılmış olan bu kavram, çağdaş fizikten tümüyle çıkarılmıştır.
Bir gözlemcinin uzay ve zaman ölçümlerinin, hareketli bir başka gözlemcinin ölçümlerine göre hangi değerleri alacağı, Lorentz dönüşümleri adı verilen matematik denklemleriyle belirlenir. Örneğin x ekseni boyunca ölçülen bağıl hareketin hızı v ise, öteki referans sisteminde,
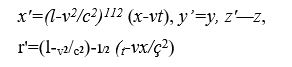
değerleri bulunur.
Özel kuramın sonuçları.
Bir eylemsiz referans sisteminin bir başka referans sistemine göre hızı arttıkça, bu sistemdeki cetveller gitgide kısalır ve saatler gitgide yavaşlar. İki sistemin birbirine göre hızı ışık hızına yaklaştıkça bu etkiler de çok büyük ölçüde artar. Referans sistemlerinin hangisinden bakılırsa bakılsın, ışığın her doğrultudaki hızının c olabilmesi için, iki sistem arasındaki göreli hızın cden fazla olmaması gerekir. Bu nedenle özel görelilik kuramına göre, referans sistemlerinin göreli hızları cden büyük olamaz: Lorentz dönüşümleri, bir referans sistemine göre bir cismin hızının, bir başka sistemde alacağı değerleri belirlemiştir. Sistemlerin birbirine göre hızı v, bir sistemdeki cismin hızı u ile gösterilirse, öbür referans sistemine göre cismin hızı
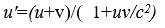 denklemiyle verilir.
denklemiyle verilir.Maddesel bir cismin kütlesi, bir kuvvetin hareket durumunda yol açtığı değişime direncinin bir ölçüsüdür. Cismin kütlesi büyüdükçe ivmesi azalır. Maddesel cismin hızı ışık hızına yaklaştıkça daha fazla hızlanmaya karşı direnci de artar ve bu hız hiçbir zaman c sınırını aşamaz. Özel kurama göre, bir cismin durgun kütlesi m işe, hareketli kütlesi
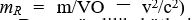 denklemiyle belirlenir. Buna görelilik kütlesi(*) de denir. Cismin kinetik enerjisi E ile gösterilirse, görelilik kütlesi ile durgun kütle arasındaki fark,
denklemiyle belirlenir. Buna görelilik kütlesi(*) de denir. Cismin kinetik enerjisi E ile gösterilirse, görelilik kütlesi ile durgun kütle arasındaki fark, 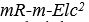 ya da genel olarak
ya da genel olarak 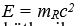 denklemleriyle gösterilir. Bunlar, kütle ile enerjinin eşdeğerliği sonucunu verirler. İki uzak olgu arasındaki zaman aralığı T, bunlar arasındaki uzaklık L olursa tüm eylemsiz referans sistemlerinde aynı değeri alacak olan
denklemleriyle gösterilir. Bunlar, kütle ile enerjinin eşdeğerliği sonucunu verirler. İki uzak olgu arasındaki zaman aralığı T, bunlar arasındaki uzaklık L olursa tüm eylemsiz referans sistemlerinde aynı değeri alacak olan 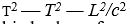 ifadesi yazılabilir. Bu nicelik, bir başka referans sisteminden elde edilen T2 L2/c2, niceliğine eşittir. Eğer T2 pozitif
ifadesi yazılabilir. Bu nicelik, bir başka referans sisteminden elde edilen T2 L2/c2, niceliğine eşittir. Eğer T2 pozitif ise, r niceliğine iki olgu arasındaki değişimsiz (zamansı) aralık adı verilir, T2 negatif ise
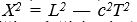 ifadesi türetilebilir ve X niceliğine değişimsiz (uzaysı) aralık denir.
ifadesi türetilebilir ve X niceliğine değişimsiz (uzaysı) aralık denir.Bir eylemsiz referans sistemi ve iki benzer maddesel cisim (ikiz) alınsın. Örneğin, özdeş tasarımlanmış iki atom saatinde, saatlerden biri sistemde sürekli durgun kalırken öbürü ilkin yüksek bir hızla birinciden uzaklaşsın ve sonra gene yüksek hızla geri dönsün. Lorentz dönüşümlerine göre, ikinci saat, yolculuğu süresince daha yavaş işleyeceğinden, döndüğünde birinciye göre geri kalmış olacaktır. Öyleyse saatlere bakılarak hangisinin durgun kalmış, hangisinin hareket etmiş olduğu ayırt edilebilir. Görelilik kuramı farklı eylemsiz referans sistemleri arasında bakışımsız ayrılıklar gözetmediğinden, bu durum görelilik kuramına aykırı gözükmektedir ve saat paradoksu ya da ikiz paradoksu olarak adlandırılır. Oysa ikinci saat için aslında bir eylemsiz referans sistemi söz konusu değildir. Çünkü, dönüş yolculuğuna başlayabilmesi için yavaşlaması, durması, ters yönde hareket etmesi ya da bir yay çizerek yön değiştirmesi gerekir. Bütün bu durumlar, ikinci saatin artı ya da eksi ivme kazanması anlamına gelir. Dolayısıyla birinci saat ile aynı eylemsiz referans sisteminde bulunmaz. Bu nedenle görelilik kuramına aykırı bir durum, bir paradoks yoktur. Hareketli parçacıklar ve atomlar üzerinde gerçekleştirilen deneyler de kuramı doğrulamaktadır.
Alman matematikçi Hermann Minkowski, iki olgu arasındaki değişimsiz aralığın, Eukleidesçi geometrideki uzaklığın kimi özelliklerine sahip olduğunu gösterdi. Birbirine dikey üç eksenden oluşan kartezyen koordinat sisteminde, iki olgu arasındaki s uzaklığı
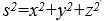 ifadesinin kareköküyle belirlenir ve bu uzaklık koordinat sisteminin seçiminden bağımsızdır. Değişimsiz aralık da, benzer biçimde, uzaydaki ve zamandaki aralıkların karelerinin toplam ve farkının kareköküne eşittir. Minkowski, bu nedenle, uzay ve zamanın tek bir dört boyutlu sürem oluşturduğunu öne sürdü; bu sürem, uzay -zaman ya da Minkowski evreni olarak adlandırılır. Uzay-zamanda değişimsiz aralık zamansı ya da uzaysı olabilir; eğer iki olgu için
ifadesinin kareköküyle belirlenir ve bu uzaklık koordinat sisteminin seçiminden bağımsızdır. Değişimsiz aralık da, benzer biçimde, uzaydaki ve zamandaki aralıkların karelerinin toplam ve farkının kareköküne eşittir. Minkowski, bu nedenle, uzay ve zamanın tek bir dört boyutlu sürem oluşturduğunu öne sürdü; bu sürem, uzay -zaman ya da Minkowski evreni olarak adlandırılır. Uzay-zamanda değişimsiz aralık zamansı ya da uzaysı olabilir; eğer iki olgu için 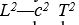 değeri sıfıra eşitse, bu aralık ışıksı olarak adlandırılır, çünkü önceki olgudan çıkan bir ışık ışını, sonraki olgudan tam bu olgu olurken geçer.
değeri sıfıra eşitse, bu aralık ışıksı olarak adlandırılır, çünkü önceki olgudan çıkan bir ışık ışını, sonraki olgudan tam bu olgu olurken geçer.GENEL GÖRELİLİK KURAMI
Fiziksel kökenleri. Genel görelilik kuramı, özel görelilik kuramının getirdiği yeni uzay ve zaman kavramlarını elektrik ve magnetik olaylar bölgesinden çıkarıp, tüm fiziğe ve özellikle kütleçekimi kuramına genişletmek gereğinden türetilmiştir.
Nevvtonun kütleçekimi etkileşmelerine getirdiği açıklamalar, olağanüstü doğrulukta sonuçlar veren en başarılı kuramlardan birini oluşturmaktadır. Newtonun kuramı, Güneşin gezegenleri ve gezegenlerin de uydularını çektiğini, bu karşılıklı çekimin uzaydaki çok büyük uzaklıklarda bile bir anda gerçekleştiğini öngörür; buna karşılık görelilik kavramları, hiçbir etkileşmenin ışık hızından daha hızlı yaylamayacağını öne sürer. Güneş sistemindeki gökcisimleri ışık hızının binde birinden düşük hızlarla hareket ettiklerinden, pratikte bunun bir önemi yoksa da, Newtonun anlık etki kavramı görelilik kuramının uzay-zaman kavramıyla temelden uyuşmazlık içindedir.
Maxwellin elektrik alanı kuramından elde edilen deneyimleri temel alan Einstein, ışık hızıyla yayılan ve Newton kuramının öngördüğü çekime hemen hemen eşit bir çekim ortamı yaratan bir kütleçekimi alanının varlığını öngördü. Bir kütleçekimi alanı kuramının matematiksel olarak elektrik ve magnetik alan kuramlarından daha kapsamlı olması gerektiği, daha başından belliydi. Elektrik alan kaynakları olan parçacık yükleri, onları ölçen aygıtların hareket durumlarından bağımsız değerlere sahiptir. Kütleçekimi alanının kaynağı olan parçacık kütlesi ise belirlendiği referans sistemine göre parçacığın hızına bağlı olarak değişir ve ayrı referans sistemlerinde ayrı değerler alır. Bu zorlaştırıcı etken, göreli kütleçekimi kuramını geliştirme uğraşısında ortaya bir belirsizlik çıkarır. Einstein bu sorunu eşdeğerlik ilkesine başvurarak çözmüştür.
Eşdeğerlik ilkesi. Bir kütleçekimi alanında, örneğin yeryüzünde, kütlesi daha büyük olan bir cisme etkiyen kuvvetin de daha büyük olduğu günlük yaşamdan bilinir. Newton belirli bir çekim alanında bir efeme etkiyen kuvvet ile o cismin kütlesi arasındaki oranın, cismin kimyasal yapısına ve başka özelliklerine bakmaksızın, bütün cisimler için aynı olduğunu ve çekim alanında serbest düşüş yapan bütün cisimlerin aynı ivmeye (hızlanma hızı) sahip olduğunu belirlemişti. Yeryüzünde bu ivme saniyede yaklaşık 9,81 mdir.
Kütleçekimi etkisiyle hızlanma, bir uzay yolculuğu örneğiyle ele alınabilir. Uzay kapsülü süzülmeye geçtiğinde, aracın, astronotların ve araçtaki bütün cisimlerin ivmesi aynıdır yani birbirlerine göre ivmeleri yoktur. Bunun sonucu olarak görünüşte ağırlıksızlık ortaya çıkar. Astronotları kapsülün tabanına bastıran bir kuvvet kalmamıştır. Serbestçe inişe geçen uzay kapsülündeki nesnelerin davranışları, kapsül yıldızlar arası uzayda tüm kütleçekimi alanlarının dışında eylemsizlik yasasına göre hareket ederken karşılaşacakları koşullardaki davranışlarından ayırt edilemez. Uzay kapsülü kütleçekimi bulunmayan bir ortamda roket motorları aracılığıyla yukarı doğru hızlandığında ise kapsül içindeki tüm cisimler, kapsül bir kütleçekimi alanında durgun durumdayken gösterecekleri davranışları gösterirler. Eşdeğerlik ilkesi, ivme kazanmış eylemsiz olmayan bir referans sistemine (örn. roketleri ateşlenmiş kapsül) gösterilen tepkiler ile kütleçekimi kuvvetleri arasında eşdeğerliği ve eylemsiz referans sistemleri ile serbest düşen yerel referans sistemleri arasındaki eşdeğerliği ortaya koyar.
Einstein, kütleçekimi alanlarının bulunduğu yerlerde, seçilen bir referans sisteminin eylemsiz olmayan karakterinden doğan etkilerle kütleçekiminin etkilerini ayırt edebilecek hiçbir yol bulunmadığını kanıtlamıştır. Genel görelilik kuramı, kütleçekimi alanının bu niteliğini temel olarak kabul etmiştir.
Uzay-zaman eğriliği. Minkowski uzay-zamanında eylemsiz referans sistemleri, Eukleidesçi geometrideki doğrulardan oluşan kartezyen koordinat sistemlerine benzer. Böyle bir koordinat sistemi bir düzleme her zaman yerleştirilebilir, ama bir küre yüzeyine uygulanamaz. Çünkü karelerden oluşan bir ızgarayı bir küre yüzeyine örtmek olanaklı değildir. Bu nedenle, düzlem düz bir yüzeydir, ama küre yüzeyi eğridir. Yüzeylerin kendi iç özelliklerinden kaynaklanan bu sınıflamaya göre silindir yüzeyi de düz bir yüzeydir, çünkü bir düzlem üzerine açındırı- labilir yani karelerden oluşan bir ızgarayla örtülebilir.
Einstein kütleçekimi alanlarının (kütleçekimi yokken düz olan) uzay-zamanı eğrilttiğini ve eylemsiz sistemlerin bu nedenle oluşturulmayacağım öne sürdü. Bir parçacığın kütleçekimi etkisiyle uzayda ve zamanda eğrilen yörüngesi, (ancak düz uzaylarda ve uzay-zamanlarda var olabilen) doğru çizgilere değil, eğrilmiş bir uzay- zamanda var olabilecek en düz eğriye karşılık gelir; böyle eğriler jeodezik olarak adlandırılır. Yerin yüzeyi gibi küresel yüzeyler üzerindeki jeodezikler, içinde bulundukları düzlemler kürenin merkezinden geçen büyük çemberlerdir. Bunlar küre yüzeyine çizilebilecek eğriliği en az çizgilerdir, ayrıca yüzeydeki iki noktayı birleştiren en kısa yolu oluştururlar. Uzay-zamanda ise jeodezikler iki olguyu (bir parçacığın geçmişindeki iki anı) arada geçen zaman en büyük olacak biçimde birleştirirler.
Bir kütleçekimi alanı, uzay-zamanın eğriliğine yol açıyorsa, bu eğrilik hesaplarından kütleçekimi alanlarına ilişkin nicelikler saptanabilir. Eğriliği belirleyen bileşenler, matematikçi Bernhard Riemannm geliştirdiği eğrilik tensörleriyle hesaplanabilir.
Kuramın doğrulanması. Genel görelilik kuramının temel taşlarından biri sayılan eşdeğerlik ilkesi çok duyarlıklı deneylerle sınanmış, doğruluğu trilyonda bir hata payıyla saptanabilmiştir.
Çeşitli gezegenlerin Güneş çevresindeki eliptik yörüngelerinin büyük eksenleri, yörünge düzleminde yavaşça döner. Merkür ün yörüngesinin yüzyıl başına 574 açı saniyelik dönüşünün 531 açı saniyelik bölümü, öbür gezegenlerin kütleçekimi etkisinden kaynaklanır. Geriye kalan 43 açı saniyelik dönme ise ancak genel görelilik kuramı ortaya çıktıktan sonra açıklanabilmiştir ve genel görelilik kuramının öngördüğü değerle kesin olarak uyuşmaktadır.
Genel görelilik, bir kütleçekimi alanı içinde bulunan ışık kaynağından yayılan ışığın dalgaboyunun büyüyeceğini, yani kırmızıya kayacağını öngörür. Bu etki, yüzeylerindeki kütleçekimi potansiyeli çok yüksek olan beyaz cüceler adı verilen yıldızlarda gözlenmiştir.
Uzay-zaman eğriliğinin bir sonucu, kütleçekimi alanlarından geçen ışık ışınlarının büküleceği ve yayılma hızlarının yavaşlaya- cağıdır. Kuramın yayımlanmasından birkaç yıl sonra tam Güneş tutulmasında Güneş diski yakınındaki bir yıldızın görüntüsünün gökte bulunması gereken yerden 1 açı saniyesinden daha küçük bir açıyla sapmış olduğunun saptanması da bu öngörüyü doğrulamaktadır.
GÖRELİLİK İLKELERİNİN UYGULAMALARI
Parçacık hızlandırıcılar. Çağdaş parçacık hızlandırıcıları, parçacıkların hızlarını ışık hızına çok yaklaştırırlar. Örneğin, milyarlarca elektronvoltluk enerjilerde çalışan elektron senkrotronlarında, yörüngedeki bir elektronun kütlesi, durgun kütlesinin 10 bin katma çıkabilir. Hızı ise ışık hızına çok yakın değerler alabilir. Bu nedenle, parçacık hızlandırıcılarının tasarımlarında görelilik etkilerinin göz önünde bulundurulması zorunludur.
Göreli parçacık fiziği. Atomaltı parçacıkların fiziği, özel görelilik kuramının ilkelerine bağlıdır. Bu ilkelerin doğrudan uygulamalarına parçacıkların yaratılış, yok ediliş ve başka parçacıklara dönüşümlerinde rastlanır. Parçacık dönüşümleriyle ortaya çıkan enerji alışverişleri, özel görelüiğin kütle ile enerjinin eşdeğerliği ilkesi uyarınca ortaya çıkar. Bir başka deyişle, böyle dönüşümlerde parçacıkların toplam durgun kütlelerinde ortaya çıkan değişim ile toplam enerji değişimi birbirlerine
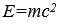 bağıntısıyla bağlıdır; bu kural evrensel olarak doğrulanmıştır. Durgun kütlesi sıfır olan foton, ışık hızıyla hareket ettiğinden, toplam enerjisinin c2ye bölünmesiyle bulunan bir görelilik kütlesine sahiptir. Bu görelilik kütlesi bir
bağıntısıyla bağlıdır; bu kural evrensel olarak doğrulanmıştır. Durgun kütlesi sıfır olan foton, ışık hızıyla hareket ettiğinden, toplam enerjisinin c2ye bölünmesiyle bulunan bir görelilik kütlesine sahiptir. Bu görelilik kütlesi bir foton ile bir parçacık etkileştiğinde fotonun doğrusal momentumunda gözlenen değişimden yola çıkılarak hesaplanabilmekte ve görelilik kuramı gene doğrulanmaktadır.
Göreli kozmoloji. Özellikle 1960lardan sonra, yeni buluşlar ve gözlem tekniklerinin gelişmesi sonucunda özel ve genel görelilik kuramlarının uygulanmasıyla evrenin yapısı ve geçmişi üzerindeki araştırmalar çok ilerlemiştir. En uzak astronomik cisimlerin ışıklarında gözlenen kırmızıya kayma olayı, genişleyen evrende bu cisimlerin bizden hızla uzaklaştıklarına işaret etmektedir. Eğer genişleme sabit hızla olmaktaysa, bu olayın
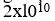 yıl önce başlamış olması düşünülmektedir.
yıl önce başlamış olması düşünülmektedir.Mikrodalgalar ile kızılötesi ışınımların sınır bölgesine düşen frekanslarda her yönden gelen fon ışınımlarının bulunuşu, evrenin geçmişte olağanüstü yoğun ve sıcak olduğu dönemlerin varlığının kanıtı sayılmaktadır. Genel görelilik kuramı kuramsal kozmolojiye evrenin bir bütün olarak düz olması gerekmediği, büyük bir olasılıkla da düz olmadığı görüşünü getirmektedir. Evrenin çok büyük (kozmolojik) ölçekte homojen ve yönsemez (özellikleri her yerde ve her doğrultu boyunca özdeş) olduğu kabul edilse bile çeşitli olasılıklar ortaya çıkmaktadır. Evren uzaysal olarak bir açık evren olabilir (düz bir evren doğal olarak açık evrendir) ya da bir küre yüzeyi gibi kendi üstüne kapalı olabilir, bu durumda sınırları da yoktur. Benzer biçimde, evrenin, zaman içinde açık ya da kapalı olduğu düşünülebilir. Zaman içinde kapalı bir evren tasavvur etmek epeyce zordur, çünkü böyle bir evrenin alışılagelmiş neden-sonuç kavramlarıyla uyuşmadığı söylenebilir. Ama bu kavramlar normal günlük yaşamdan elde edilmiş kavramlardır, milyarlarca yıl içeren bir zaman ölçeğinde geçerli olmayabilirler. Çeşitli kozmolojik modeller ortaya konmuş ve bunlar kuramsal olarak incelenmiştir, ama gözlem sonuçlarının bu modellerden herhangi birini doğruladığı söylenemez. Gözlemlerden elde edilen bilgiler, evrenin geçmişte bir ateştopu (olağanüstü yoğun ve sıcak madde) durumunda iken genleşerek oluştuğu görüşünü içeren modelleri destekleyici niteliktedir.
Son düzenleyen Safi; 1 Temmuz 2016 01:12

 İzafiyet Teorisi (E=mc²)
İzafiyet Teorisi (E=mc²)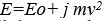 formülüyle verilirdi. Özel görelilik kuramında p ve E için bu formüller sırasıylap E=mc2 biçimini almıştır; burada c ışık hızı (saatte 300.000 km) ve m cismin durgun kütlesidir (yani, cismin hareketsiz durumundaki kütlesi). Bir cismin görelilik kütlesi (m/?) çoğunlukla
formülüyle verilirdi. Özel görelilik kuramında p ve E için bu formüller sırasıylap E=mc2 biçimini almıştır; burada c ışık hızı (saatte 300.000 km) ve m cismin durgun kütlesidir (yani, cismin hareketsiz durumundaki kütlesi). Bir cismin görelilik kütlesi (m/?) çoğunlukla 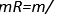
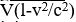 olarak verilir. Buradan, tüm hızlar için
olarak verilir. Buradan, tüm hızlar için 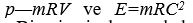 bağıntıları elde edilir. Bir cismin hızı ışık hızına yaklaştıkça görelilik kütlesi de sonsuza yaklaşır, bu nedenle de cisme ne kadar momentum ve enerji eklenirse eklensin, hızı her zaman cnin altında kalır.
bağıntıları elde edilir. Bir cismin hızı ışık hızına yaklaştıkça görelilik kütlesi de sonsuza yaklaşır, bu nedenle de cisme ne kadar momentum ve enerji eklenirse eklensin, hızı her zaman cnin altında kalır.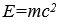 eşitliğiyle verilebilecek bir kütle enerjisi taşıdığını gösterir. Bu enerji kütle yitimiyle başka enerji biçimlerine dönüşebilir. Buna karşılık, elektromanyetik enerji, kütle biçiminde maddeye dönüşebilir: bu iki süreç, nükleer tepkimelerde sürekli olarak gözlemlenir ve görelilik kuramı için en iyi doğrulamayı oluşturur.
eşitliğiyle verilebilecek bir kütle enerjisi taşıdığını gösterir. Bu enerji kütle yitimiyle başka enerji biçimlerine dönüşebilir. Buna karşılık, elektromanyetik enerji, kütle biçiminde maddeye dönüşebilir: bu iki süreç, nükleer tepkimelerde sürekli olarak gözlemlenir ve görelilik kuramı için en iyi doğrulamayı oluşturur.
