Ziyaretçi
Matematik Bilimi
Tarihi
Bugün okullarımızda öğretilen matematiğin ortaokul 2. sınıfa kadarki kısmi olarak değerlendirebiliriz. Aynı dönemde Mezopotamya'da matematik biraz daha ileridir; onların bildikleri matematiğin düzeyi de lise 2. sınıf matematiği düzeyidir. Matematik, günlük hayatin ihtiyaçlarına (takvim belirlemek, muhasebe ve mimari hesaplar gibi) yönelik, henüz sanat düzeyine ulaşmamış, zanaat düzeyinde bir uğraşıdır. Formel ifadeler, formüller ve akil yürütmeye dayalı ispatlar yoktur. Bulgular deneye dayalı ve işlemler sayısaldır. İkinci dönem, M. Ö. 6. yy'dan M. S. 6. yy'a kadar uzanan Yunan matematiği dönemidir. Matematiğin nitelik değiştirdiği, zanaat düzeyinden sanat düzeyine geçtiği dönemdir. Yunan matematiğinin başlangıcında Mısır ve Mezopotamya varsa da Yunan döneminde, matematiğin günümüze kadar yönü belirlenmiş, bir sıçrama yapılmıştır.
Matematiğe en önemli katkılar Platon'un akademisinde ve İskenderiye’deki Museum'da yetişen bilim adamlarından gelmiştir. Yunan matematiği esasta 'sanat için sanat' anlayışıyla yapılan ve günümüz manasında modern bir matematiktir. Üçüncü dönem, M.S. 6. yy'dan 17. yy'in sonlarına kadar olan dönemdir. Bu dönemde, matematiğin yaşadığı dünya İslam dünyası ve Hindistan’dır. Müslümanların matematiğe katkısı büyük bir tartışma konusudur. Kimilerine göre, Müslümanların matematiğe, Yunan matematiğini yaşatmak ve Batı’ya transfer etmekten öte, bir katkıları olmamıştır. Kimilerine göre ise, Müslümanların matematiğe özgün kalkılan olmuştur. (Bu katkılar Avrupalı matematikçiler tarafından tekrar bulunmuş ya da göz ardı edilmiştir.) Müslümanların matematiğe katkısı yeterince araştırılmamıştır. Son yıllarda yapılan araştırmalar, matematiğin en önemli bulusu olan türevin, Avrupalılardan 500 yıl önce Azerbaycanlı Şerafettin Al-Tusi tarafından bulunmuş olduğunu ortaya çıkarmıştır. Tarihi olaylar- Haçlı seferleri, Moğol istilası ve dâhili olaylar-, İslam dünyasının nakli bilimlere geçmesine ve sonuç olarak bilimin yerini safsatanın almasına neden olmuştur. 16. yy' da matematikte tek söz sahibi Avrupalılardır.
Dördüncü dönem, 1700–1900 yılları arasını kapsar ve 'Klasik Matematik Dönemi' olarak bilinir. Matematiğin 'Altın Çağları' olarak da anılır. Büyük hipotez ve teorilerin ortaya çiktigi, matematiğin kullanım alanının bütün bilim dallarını kapsayacak şekilde genişlediği bir dönemdir. Matematik, bütün pozitif bilimlerin temelim oluşturacak bir konuma gelmiştir. Bugün üniversitelerde okutulan matematiğin büyük bir kısmi bu dönemin ürünüdür. Besinci dönem, 1900'lü yılların basından günümüze uzanan, 'Modern Matematik Dönemi' olarak adlandırılan dönemdir. Modern matematik, klasik matematiğin anayasal bir tabana oturtulmuş seklidir. 1900'lü yılların başına gelindiğinde, matematik büyük bir kompleksiteye ulaşmıştı.
Böylesi karmaşık bir sistemde alışılageldiği şekilde matematik yapmak, 'bir ispat niçin geçerlidir; ispatin da ispati gerekli midir?' gibi matematiğin temellerini sorgulayan sorunları ortaya çıkarmıştır. Matematik deneysel bir bilim olmadığı için, nihai yargıyı deneye bırakmak olanağı yoktur. Bu sorunların, 'meşru' bir zeminde çözüme ulaştırılacağını anlayan matematikçiler, matematiği tutarlı yasalara dayalı bir temele oturtma çabasına giriştiler. Modern matematik bu uğraşının ürünüdür. Modern matematiğin en önemli özellikleri, önceki dönemlere kıyasla, çok daha soyut, göreceli ve kuramsal olusudur. Matematik çok hızlı gelişen, çok yüksek bir teknik düzeye erişmiş, elde edilen bilgilerin üst üste yığıldığı, bir bilginin diğeri tarafından kullanımdan kaldırılmadığı, bu nedenle de gittikçe zorlasan ama bir o kadar da çekici, ancak tutku ile yapılabilen bir bilimdir.
Sponsorlu Bağlantılar
İlk matematikçi belki de, sürüsündeki hayvanları saymaya çalışan bir çobandı. Büyük bir olasılıkla da ilk bulunan sayı "çok" dur. Sonra 2, daha sonra da 1 bulunmuş olabilir. Ama en zor bulunan 0 (sıfır)'dır. Sıfır sayısı M.S. 7. yy. da kullanılmaya başlanmıştır. Bu belki de insanlığın en büyük buluşudur. Sayma sisteminin ne kadar uzun sürede geliştiği, ilkel toplumlarda nasıl doğduğu, yakın zamanlarda ortaya çıkarılan bir takım ilkel kavimlerde gözlenebilmiştir.Matematik, bir yönüyle resim ve müzik gibi bir sanat, bir yönüyle bir dil ve başka bir yönüyle de tabiatı anlamaya yönelik yöntemler manzumesidir. Matematiğin yazılı belgelere dayalı 4500 yıllık bir tarihi vardır. Bu zaman dilimi içinde, matematiğin gelişimi 5 döneme ayrılır. Birinci dönem, başlangıçtan M.Ö. 6. yüzyıla kadar, Mısır ve Mezopotamya'da yapılan matematiği kapsar. Mısır’da bilinen matematik, tam ve kesirli sayıların 4 işlemi, bazı geometrik şekillerin alan ve hacim hesaplarıdır.
Avustralya'da bir kavim 1, 2, 3, çok diye dört sayı biliyor, fakat bütün çocuklarını sayabiliyormuş; ilk doğan erkek çocuğun her ailede adı aynıymış, 2 ve 3. için de böyle ve kız çocukları için de benzer uygulama yapılıyormuş. Bu şekilde bir çocuğun kaçıncı erkek ya da kaçıncı kız çocuğu olduğunu anlıyorlarmış. Ama hayvanlarını sayamıyorlarmış.
Bir başka kavimde, en çok koyunu olan kişi, kavmin reisi olarak seçiliyormuş. Seçimde iki aday varsa yan yana iki ağıldan koyunlar birer birer çıkarılıyor ve ilk tükenen seçimi kaybediyormuş.
Oldukça erken çağlarda, insanlar aynı cins nesneleri karşılaştırarak, büyüklüklerini ölçerek ve aralarında oranlar kurarak matematiğe başlamışlardır. Kemik üzerine, kum üzerine çizerek ya da ipe düğüm atarak bir büyüklüğü belirtmeye çalışmışlardır.
Sümer çobanları her hayvanı kilden bir koni ile gösterip, bu konileri kıldan bir torba ya da kilden bir küp içinde biriktirerek ölüm, doğum, alım, satım hesaplarını tutmuşlar. Mezopotamya'da küp üzerine benzer şekiller çizilmiş. Böylece M.Ö.3000'e doğru ilk yazılı sayılarla karşılaşmış oluyoruz.
Tarımla uğraşan en ilkel kabileler bile, mevsimlerle ilgili bilgileri edinmek zorundaydılar. Örneğin, Eski Mısır'da Nil taşkınlarının ne zaman olacağını bilmek çok önemliydi. Taşkından sonra kaybolan toprak sınırlarını yeniden hesaplamak gerekiyordu. Geometri ve astronomi bu sayede gelişti.
Fenikeliler gibi tüccar-denizci toplumların ekonomileri bir muhasebe sistemi gerektirmiştir. Miras bölüşümü ve denizcilik zanaatı için aritmetiğin, geometri ve astronominin bilinmesine gereksinim vardı. Böylece, toplumsal yaşamın gerektirdiği matematiksel gelişme belirli bir düzeye erişti. Daha sonra matematik sadece uzmanların anlayabildiği bir meta haline geldi; insanlar olgularla yetinmeyip ispata yöneldiler. Bu durum, en belirgin bir biçimde eski Yunanistan’da ortaya çıktı. İspat etmenin ön plana çıkması ile matematik günümüzdeki gelişmişlik düzeyine ulaştı.
Eski Mısır'da Pitagor (Pisagor) teoremi biliniyordu. Ancak ispatı önemliydi ve ilk olarak Eski Yunanistan'da ispat edildi.
Hindistan'da tüccar bir toplum vardı ve teoriden çok pratiğe önem veriliyordu. Ancak ticarette borç problemlerinin çözümü için negatif sayılara gereksinim vardı. Böylece, bildiğimiz sayı sistemi, dolayısıyla Analiz ve Cebir gelişti. Bu kavramlar daha sonra Araplar aracılığıyla Avrupa'ya geçti.
Oldukça erken çağlarda başlayan ve Babil, Asur, Mısır, Yunan uygarlıklarında genel toplumsal yaşamın gerektirdiği ölçüde gelişen matematik Avrupa’ya oldukça geç ulaşabildi. Ancak belirli bir gelişmişlik düzeyinde Avrupa’ya ulaşan matematik, 15. yy. 'a kadar sadece az sayıda din adamı ya da filozofun elinde birer eğlence ya da güç gösterisi olmaktan öteye gidemedi.15.yy tam sayılarla toplama ve çıkarma, Avrupa’nın ancak birkaç üniversitesinde öğretilebiliyordu. Çarpmayı öğrenmek için İtalya’nın önemli bir kaç üniversitesinden birine gitmek gerekiyordu. Geometri olarak, Öklid geometrisinin basit konuları, sadece büyük filozofların tartışma konusuydu. Bölme işlemi ise 16.yy getirdiği bir yenilikti.
Matematikte bilim kavramı ancak 17. yy. da kullanılmaya başlandı. 20.yy başlarında analiz, cebir ve geometri belirli bir düzeye erişebildi; kümeler teorisi kuruldu, matematik büyük bir gelişme hızı kazandı ve ilerlemeğe devam ediyor.
Bugün okullarımızda öğretilen matematiğin ortaokul 2. sınıfa kadarki kısmi olarak değerlendirebiliriz. Aynı dönemde Mezopotamya'da matematik biraz daha ileridir; onların bildikleri matematiğin düzeyi de lise 2. sınıf matematiği düzeyidir. Matematik, günlük hayatin ihtiyaçlarına (takvim belirlemek, muhasebe ve mimari hesaplar gibi) yönelik, henüz sanat düzeyine ulaşmamış, zanaat düzeyinde bir uğraşıdır. Formel ifadeler, formüller ve akil yürütmeye dayalı ispatlar yoktur. Bulgular deneye dayalı ve işlemler sayısaldır. İkinci dönem, M. Ö. 6. yy'dan M. S. 6. yy'a kadar uzanan Yunan matematiği dönemidir. Matematiğin nitelik değiştirdiği, zanaat düzeyinden sanat düzeyine geçtiği dönemdir. Yunan matematiğinin başlangıcında Mısır ve Mezopotamya varsa da Yunan döneminde, matematiğin günümüze kadar yönü belirlenmiş, bir sıçrama yapılmıştır.
Matematiğe en önemli katkılar Platon'un akademisinde ve İskenderiye’deki Museum'da yetişen bilim adamlarından gelmiştir. Yunan matematiği esasta 'sanat için sanat' anlayışıyla yapılan ve günümüz manasında modern bir matematiktir. Üçüncü dönem, M.S. 6. yy'dan 17. yy'in sonlarına kadar olan dönemdir. Bu dönemde, matematiğin yaşadığı dünya İslam dünyası ve Hindistan’dır. Müslümanların matematiğe katkısı büyük bir tartışma konusudur. Kimilerine göre, Müslümanların matematiğe, Yunan matematiğini yaşatmak ve Batı’ya transfer etmekten öte, bir katkıları olmamıştır. Kimilerine göre ise, Müslümanların matematiğe özgün kalkılan olmuştur. (Bu katkılar Avrupalı matematikçiler tarafından tekrar bulunmuş ya da göz ardı edilmiştir.) Müslümanların matematiğe katkısı yeterince araştırılmamıştır. Son yıllarda yapılan araştırmalar, matematiğin en önemli bulusu olan türevin, Avrupalılardan 500 yıl önce Azerbaycanlı Şerafettin Al-Tusi tarafından bulunmuş olduğunu ortaya çıkarmıştır. Tarihi olaylar- Haçlı seferleri, Moğol istilası ve dâhili olaylar-, İslam dünyasının nakli bilimlere geçmesine ve sonuç olarak bilimin yerini safsatanın almasına neden olmuştur. 16. yy' da matematikte tek söz sahibi Avrupalılardır.
Dördüncü dönem, 1700–1900 yılları arasını kapsar ve 'Klasik Matematik Dönemi' olarak bilinir. Matematiğin 'Altın Çağları' olarak da anılır. Büyük hipotez ve teorilerin ortaya çiktigi, matematiğin kullanım alanının bütün bilim dallarını kapsayacak şekilde genişlediği bir dönemdir. Matematik, bütün pozitif bilimlerin temelim oluşturacak bir konuma gelmiştir. Bugün üniversitelerde okutulan matematiğin büyük bir kısmi bu dönemin ürünüdür. Besinci dönem, 1900'lü yılların basından günümüze uzanan, 'Modern Matematik Dönemi' olarak adlandırılan dönemdir. Modern matematik, klasik matematiğin anayasal bir tabana oturtulmuş seklidir. 1900'lü yılların başına gelindiğinde, matematik büyük bir kompleksiteye ulaşmıştı.
Böylesi karmaşık bir sistemde alışılageldiği şekilde matematik yapmak, 'bir ispat niçin geçerlidir; ispatin da ispati gerekli midir?' gibi matematiğin temellerini sorgulayan sorunları ortaya çıkarmıştır. Matematik deneysel bir bilim olmadığı için, nihai yargıyı deneye bırakmak olanağı yoktur. Bu sorunların, 'meşru' bir zeminde çözüme ulaştırılacağını anlayan matematikçiler, matematiği tutarlı yasalara dayalı bir temele oturtma çabasına giriştiler. Modern matematik bu uğraşının ürünüdür. Modern matematiğin en önemli özellikleri, önceki dönemlere kıyasla, çok daha soyut, göreceli ve kuramsal olusudur. Matematik çok hızlı gelişen, çok yüksek bir teknik düzeye erişmiş, elde edilen bilgilerin üst üste yığıldığı, bir bilginin diğeri tarafından kullanımdan kaldırılmadığı, bu nedenle de gittikçe zorlasan ama bir o kadar da çekici, ancak tutku ile yapılabilen bir bilimdir.
Derleme

 Matematik Bilimi
Matematik Bilimi
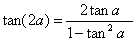
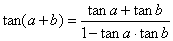
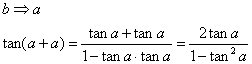
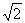 irasyoneldir.
irasyoneldir. 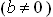 ve a ve b'nin ortak çarpanları olmadığını kabul edebiliriz.
ve a ve b'nin ortak çarpanları olmadığını kabul edebiliriz. 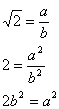
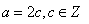
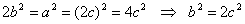
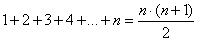
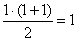

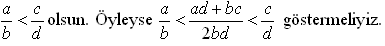
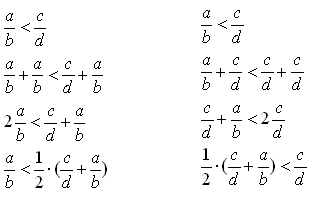
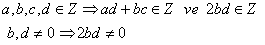
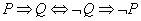
 N şeklinde yazılabilir.
N şeklinde yazılabilir. 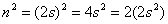
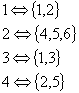

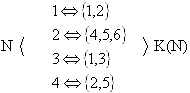

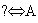

 ) harfi ile ifade edilir. Doğal sayılar
) harfi ile ifade edilir. Doğal sayılar  N olarak tanımlanan hiçbir n için (önemsiz) tam sayı çözümü yoktur.
N olarak tanımlanan hiçbir n için (önemsiz) tam sayı çözümü yoktur. 
